如何计算 CAD 几何文件的投影面积

你有没有遇到过想要计算 CAD 几何文件的投影面积的时候？这在很多情况下都很有用，例如快速估计空气动力阻力。如果你只需要计算几个方向上的投影面积，有好几种方法可以做到；但是，如果你想计算所有可能方向上的投影面积怎么办？今天，我们将介绍一种计算和使用这类数据的有效方法。

几种简单的方法

假设有一个复杂的 CAD 几何图形，我们首先要考虑的是：这个几何图形沿特定方向的投影面积是多少？有几种方法可以做到这一点？第一种方法，我们可以使用广义投影算子。这种方法需要围绕整个几何图形绘制一个框，如果想要获得良好的分辨率，就必须进行非常精细的网格划分。由于在整个域上进行网格划分和积分的成本很高，这种方法可能非常耗时。第二种方法是 COMSOL 6.0 中的新功能，即三维模型投影功能。这个新功能可以使我们在空间中绘制工作平面并将三维 CAD 几何文件投影到该工作平面上，然后直接测量这些投影的面积。这种基于 CAD几何文件的方法要快得多，并且不需要任何网格划分，但是需要使用 COMSOL 软件的CAD 导入模块、设计模块或 LiveLink™ 产品。如果我们想要计算沿多个不同任意方向的投影面积，上述这两种方法都比较繁琐。

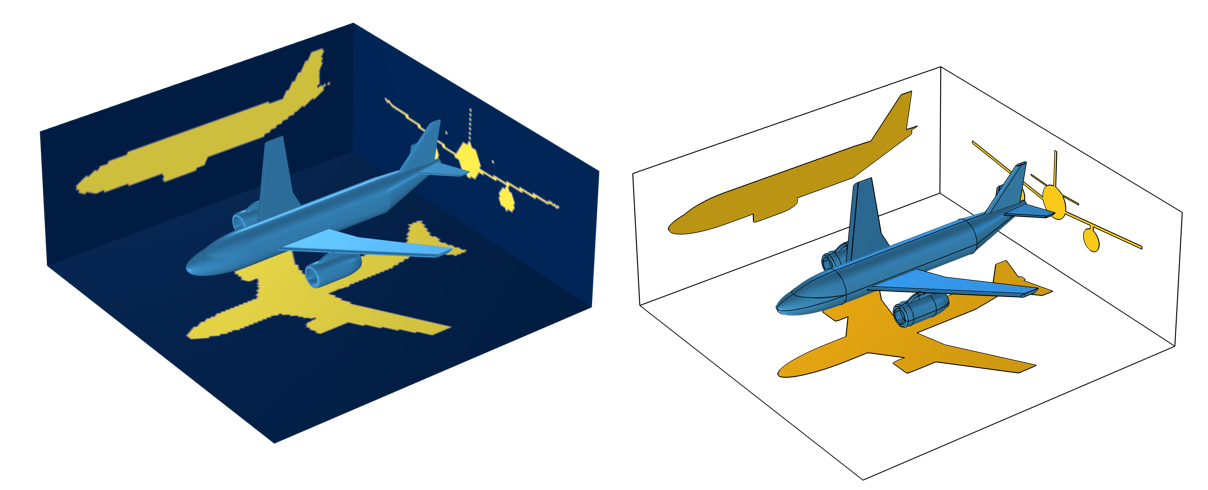
确定投影面积的两种方法： 使用 广义投影 算子，其结果取决于网格（左）；使用 投影功能，在一组工作平面上创建投影表面（右）。

一种更通用的方法

相比对 CAD 几何文件划分体网格或添加其他 CAD 操作，我们可以利用投影区域的定义，即：

其中，对于那些沿视线方向可见的表面，\beta 是视线与表面法线之间的夹角。

对表面进行积分很容易，但是如何评估项 \cos \left( \beta \right)？事实证明，当使用无限距离 外部辐射源照射时，我们可以通过 表面对表面辐射 接口获得该项。计算这个项只需要部分面网格，而非体网格。使用此接口甚至不需要求解表面到表面的辐射，因为这种带有阴影的入射外部通量是作为预处理步骤计算的。因此，我们可以简单地对所有表面上的外部通量进行积分，然后除以标称入射通量，就可以得到在 外部辐射源 接口中输入的任何方向的投影面积。由于默认使用四阶高斯积分，因此可以使用相当粗的网格。

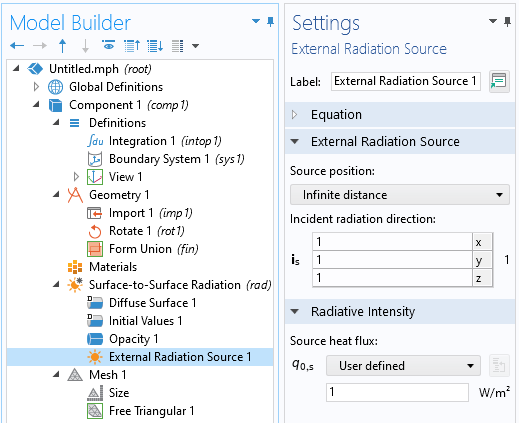
外部辐射源特征可用于设置几何体的光照以计算投影面积。

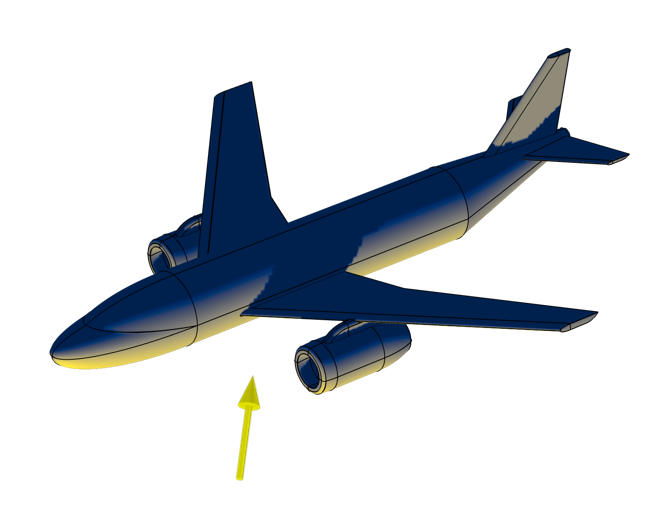
对通过 外部辐射源 特征预先计算的入射通量进行积分可以获得投影面积。注意机翼的阴影。

在所有方向上提取和使用投影面积数据

通常，我们需要从各个方向提取投影区域。现在我们可以简单地对任何感兴趣的入射方向重新计算上述积分，但计算成本将非常高。

相反，想象物体周围有一个球体，并在该球体上选择有限数量的方向来照射目标。在这些有限的方向集之间，我们可以在整个球体表面上使用线性内插法。但是，在选择这些方向之前，值得一提的是，投影区域将关于通过周围球体中心的任何平面对称。本文中使用的 CAD 几何图形关于中平面对称，所以利用这两个对称性，只考虑位于空间正 xy 象限的四分之一球体就可以了。

接下来，进行以下步骤：

1. 创建几何，利用 CAD 零件的对称性，用有限数量的点定义观察方向
2. 计算沿这些方向的投影横截面积
3. 将数据插值到所有中间方向
4. 提取这些数据

首先，我们创建一个非常特殊的几何图形，如下图所示。该几何图形看起来像一个四分之一球体的网格，它是通过首先单独创建一个单位球体的一部分的网格，导出该网格，然后将其导入模型的第二个 组件 来创建的。导入的设置是这样的，表面网格的每个单元都是一个单独的表面，每个节点都是一个几何点。该表面位于空间的正 xy 象限。

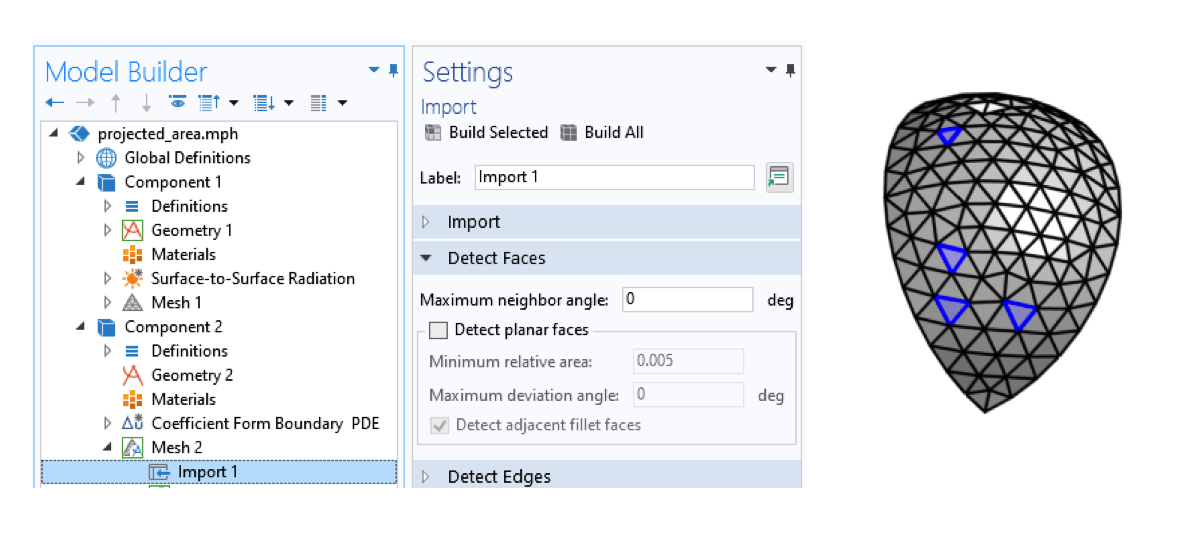
导入设置的网格，使每个单元代表不同的面。

这些点中的每一个都将代表一个采样方向，我们将评估其投影面积。在这些点之间的每个三角形块上，我们将使用线性有限元基函数对区域进行线性插值，以便可以从任何入射角近似投影区域。

为此，我们在四分之一球模型的所有表面上添加 系数形式偏微分方程接口，将离散化设置为线性，并将因变量的名称设置为 AREA。

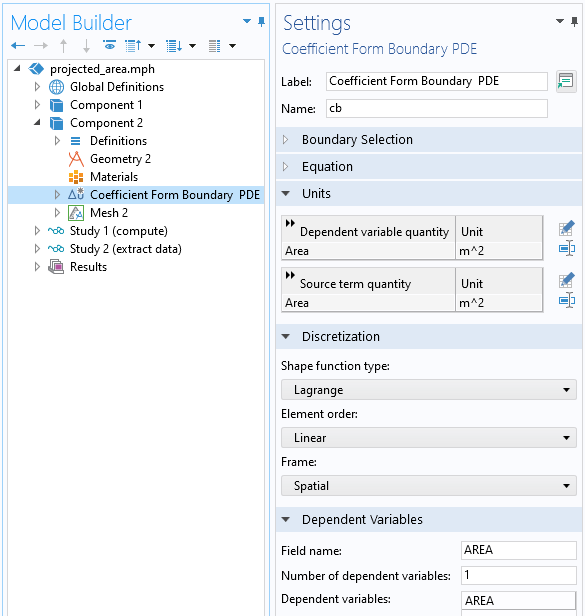
设置 系数形式偏微分方程接口将实现插值。

在这个接口中，我们将对几何中的所有点施加 逐点约束 特征，这样就可以对问题进行完全约束，因为所有的节点点都是几何点。这些设置的最终效果是所有其他物理设置都无效，并可以保留它们的默认值。我们将得到每个曲面拐角处的约束节点值之间的线性插值解。

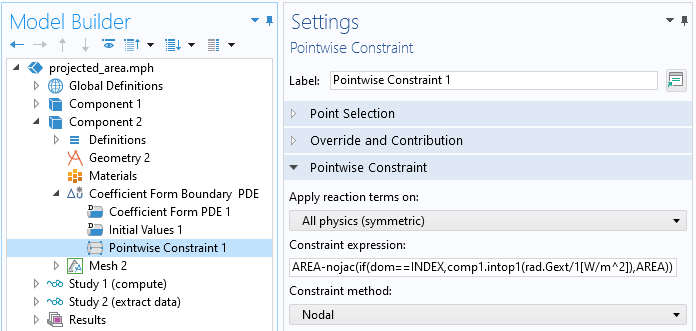
对模型上的所有点施加 逐点约束特征。

由于需要在每个点设置离散观察方向的投影面积，因此我们使用了以下约束表达式：

AREA-nojac(if(dom==INDEX,comp1.intop1(rad.Gext/1[W/m^2]),AREA))

展开这个表达式，它设置了 AREA每个点的值。首先，整个表达式必须等于 0，因此 AREA 被设置为等于 nojac() 算子的表达式。这个算子意味着其中的表达式没有增加雅可比贡献，有关这个运算原理的更多详细信息，请参阅关于通过符号微分加速模型收敛的博客文章。在这个算子中是 if(logical expression, true, false)语句。这个语句以逻辑表达式 dom==INDEX 开头。每个几何对象（域、边界、边或点）都有一个与之关联的唯一整数：它的域索引 dom。在我们即将进行的研究中，将对这个几何图形中所有点的全局参数 INDEX 进行辅助扫描。

在扫描期间，当逻辑表达式的计算结果为假时，AREA 变量保持不变。当逻辑表达式为真时，得到投影面积，即截获通量除以入射通量的积分。积分算子 comp1.intop1() 被定义在我们的第一个组件中，覆盖 CAD几何文件的所有暴露表面。但是，当计算这个积分时，第一个分量中的 外部辐射源 特征如何得出与第二个分量中的点相关联的方向？我们在第二个分量中的所有点上使用第二个积分耦合变量，并在外部辐射源 方向场中使用它：

comp2.intop2(x[1/m]*(dom==INDEX))

解读这个表达式的方法是：评估第二个组件中的所有点，即 x 位置（或 y-或 z 位置），然后乘以 (dom==INDEX)，结果将是 0 或 1。也就是说，我们将仅对当前索引的点评估朝向该点的光照矢量，如下面的屏幕截图所示。

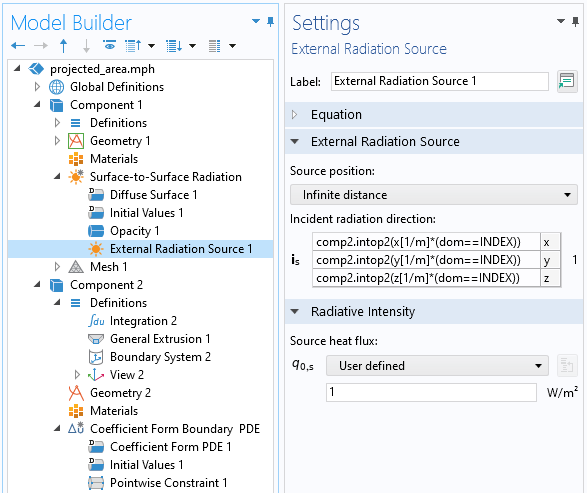
在第一个组件中，入射辐射方向是根据第二个组件中的几何定义的点位置来设置的。

接下来，我们要扫描索引变量的所有值，我们通过包含辅助扫描的稳态研究步骤 来完成。在这项研究中，我们不需要求解表面到表面的辐射，因为入射通量是一个预处理步骤。

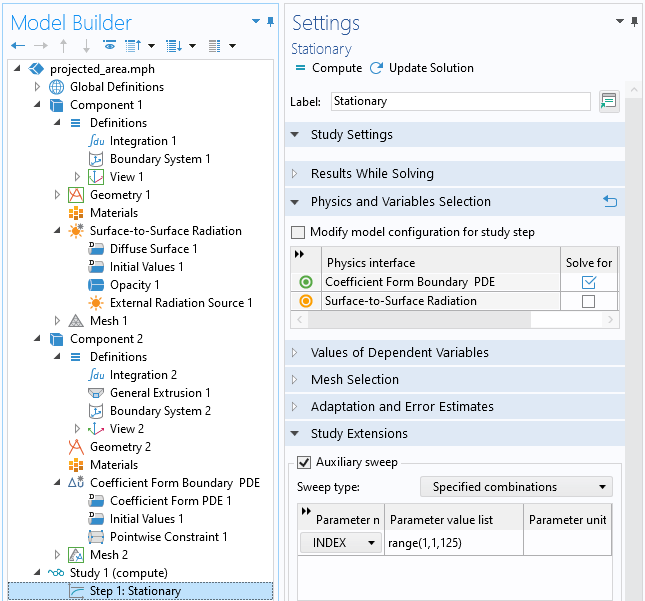
扫过索引变量将获得投影面积。

由于只有扫描中的最后一个值包含所有结果，因此我们可以弃除最后一个解之外的所有内容。这可以通过 组合解 研究步骤完成，如下面的屏幕截图所示。

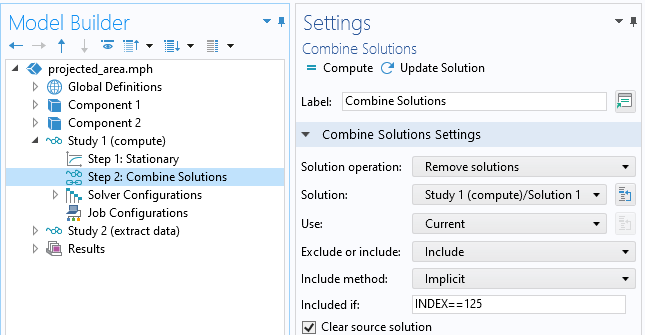
使用 组合解 特征仅保留扫描中的最后一个解。

接下来，为了举例说明如何使用这些数据，我们用一个具有 瞬态 步骤的研究来说明。在该研究中，我们将根据与飞机轴对齐的球坐标系在球体表面上追踪一个点，并且向上定义 \phi 和 \theta 角。

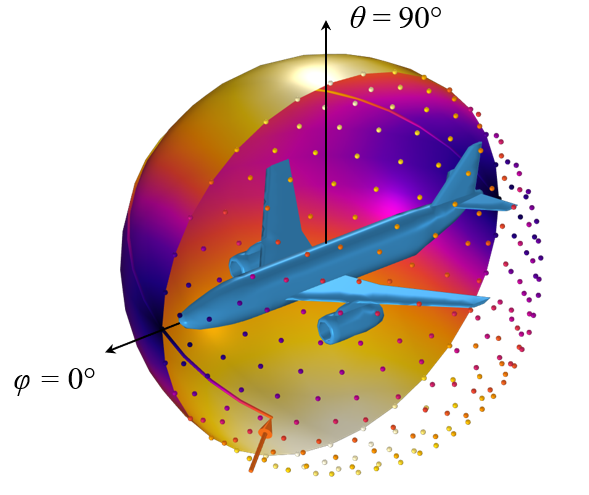
CAD 模型和沿离散方向的投影区域，由一组点表示，以及在一个表面上的插值。沿着在该表面上追踪的一条线的场值可以通过球坐标系上的 广义拉伸算子进行评估。

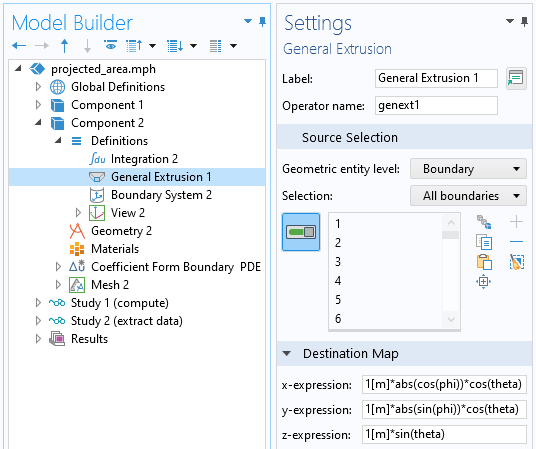
通过广义拉伸 算子从球体表面的插值数据中提取数据。

对于球坐标系，要从该球体上的任意位置提取数据，我们可以将广义拉伸算子 用作动态探针，通过输入目标映射 表达式的变量，来说明解对称性。

结束语

有多种方法可以计算 CAD几何文件的投影面积。在本文介绍的三种方法中，使用 广义投影 算子的计算成本最高，因为它在一个域上集成并且需要在周围域中使用精细的网格。因此，只有在不能使用其他两种方法时才使用它。第二种方法是基于 CAD 的操作，即使用 投影 特征。虽然这种方法简单、准确并且不需要划分网格，但需要手动设置每个投影方向。最后一种方法，使用 表面对表面辐射 接口是最复杂的设置，但在重用数据以进行进一步的基于方程的建模方面，提供了极大的灵活性。点击下方按钮，下载关于此方法的教程模型文件：