
在上一篇博客中,我们介绍了如何计算 0D 和 1D 线弹性结构的刚度。今天,我们将在此基础上,介绍如何在 2D 和 3D 中对线弹性结构进行建模。此外,我们还将演示另一种计算刚度的方法。
包括泊松效应和剪切模量
在本系列博客的第 1 部分中,我们向您演示了通过 Timoshenko 理论纳入的剪切效应如何影响刚度。 这篇文章,我们尝试在这个模型中纳入另一种真实效应,即当梁沿其长度方向被拉伸时,它的横截面积将减小,也就是我们所熟知的泊松效应。横向应变和轴向应变之间的比率由被称为泊松比(\nu)的材料属性表示。
一般来说,我们使用将应力 {σ} 和应变 {ε} 关联起来的材料的刚度矩阵 [C],将泊松效应纳入线弹性变形的物理描述中。为了考虑沿不同方向的轴向分量和剪切分量,对胡克定律进行了修改,它的广义形式可以写成:
请注意,材料的刚度矩阵 [C] 是一种材料属性,与我们之前介绍的结构(或设备)刚度(k)相反。
对于各向同性线性弹性材料,材料刚度矩阵的分量 [C] 可以仅使用材料的杨氏模量和泊松比进行计算,因为剪切模量是这两个参数的函数。对于正交各向异性材料,我们需要为杨氏模量、泊松比和剪切模量指定唯一值。对于一般的各向异性线性弹性材料,刚度矩阵可以包含多达 21 个独立的材料参数,这些参数同时考虑了泊松效应和沿不同方向的剪切效应。尽管我们的示例模型使用的是各向同性材料,但文中讨论的想法也适用于正交各向异性和各向异性材料。
现在,让我们看看如何将这些效应纳入不同空间维度的梁模型中。我们将使用 0.3 的泊松比(剪切模量为 ~77GPa)进行所有计算。
2D 模型
在对梁进行 2D 建模时,我们可以选择平面应变 或平面应力 假设。在 COMSOL Multiphysics 中,可以选择 2D 空间维度和固体力学 接口模拟 2D 平面应力和平面应变的情况。该接口提供了一个下拉菜单,可以在“平面应力”和“平面应变”条件之间切换。
平面应变选项
“平面应变”选项适用于只有面内轴向力、剪切力和弯曲力作用在结构上并产生面内应变的情况。假设面外应变分量为零,例如在平面外方向上完全受约束的结构示例。因此,对于梁建模示例,这不是一个合适的选择。在“平面应变”公式中,COMSOL 软件求解平面内位移 u 和 v。
平面应力选项
“平面应力”选项适用于只有面内轴向力、剪切力和弯曲力作用在结构上并产生面内应力的情况。假设面外应力分量为零。 在“平面应力”公式中,COMSOL Multiphysics 求解面内位移 u 和 v,以及面外应变 (wZ)。对于各向异性材料,它还求解面外位移梯度 uZ 和 vZ ,这就是为什么在 COMSOL Multiphysics 中,甚至可以使用 2D “平面应力”接口对各向异性材料建模,只要边界条件支持平面应力假设。对于这个假设,可以使用多种边界条件组合,例如梁一端被施加了滚子边界条件,而另一端处于自由状态。

边界条件显示承受轴向载荷的梁的“理想的”平面应力条件。左侧的滚子边界帮助获得恒定的轴向应力值 σxx。为了防止产生面内平移,使用滚子边界中心的一个几何点约束 y 轴位移 (v)。
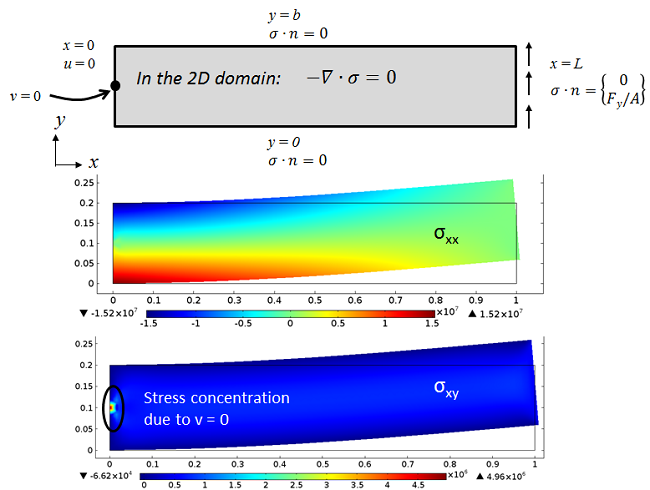
承受横向载荷的同一个“理想的”平面应力梁。与预期的情况一样,弯曲应力 σxx 呈现出平滑的变化,但剪切应力 σxy 在该点周围是奇异的,其中 v 受到约束。
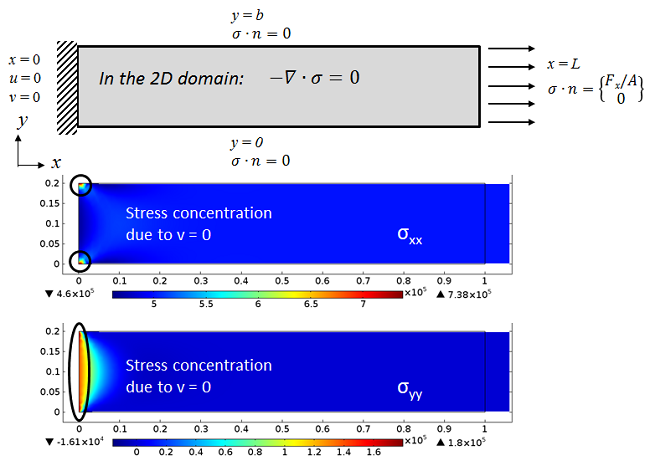
采用平面应力假设的模拟,边界条件显示一端固定一端自由的梁承受轴向载荷。由于限制了横向位移,轴向应力 σxx 在边角处是奇异的。在相同的约束下,由于垂直方向上的收缩被抑制了,σyy 也非零。
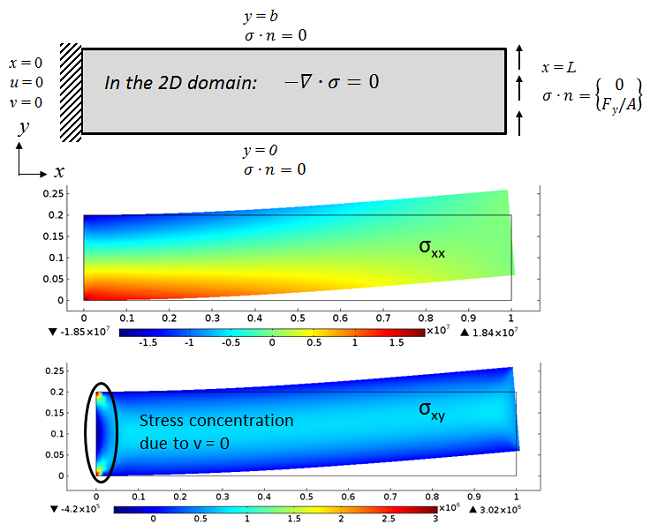
与上述相同的承受横向载荷的一端固定一端自由的梁。与预期一样,弯曲应力 σxx, 显示出平滑的变化,但其最大值略高于从“理想的”梁中获得的值。 这是因为约束横向位移会产生额外的刚度。由于相同的约束,梁的中平面上方和下方的 σxy 也是奇异的。
上图表明,采用平面应力假设只能对一端固定一端自由的梁进行“近似”建模。请注意,在 2D 模型中,局部y轴可以与表示 3D 空间笛卡尔坐标系的 y 轴或 z 轴对应,这取决于我们是否在 2D 平面内表示 xy 平面或 xz 平面。
类似地,2D 模型中的横向位移 v 也可以表示 3D 模型的横向位移 v 或 w,这取决于我们是否表示 xy 平面或者 xz 平面。我们可以使用这个信息来计算弯曲刚度 kyy 和 kzz,通过求解模型两次:一次使用高度 b(0.2m),然后使用高度 t(0.1m)。
接下来,让我们看看这些理想的和实际边界条件对由 2D 模型计算的刚度的影响:
| kxx [N/m] | kyy [N/m] | kzz [N/m] | |
|---|---|---|---|
| 一端滚子约束一端自由 | 4×109 | 3.86×107 | 9.91×106 |
| 一端固定一端自由 | 4.01×109 | 3.89×107 | 9.94×106 |
表中的数值表明,与理想的滚子约束相反,真实的固定约束会导致刚度值略高,因为固定端附近具有局部刚度效应。请注意,对于这两种情况,由于 2D 模型中考虑了额外剪切柔度(即考虑剪切变形),弯曲刚度低于欧拉-伯努利梁的弯曲刚度,这些结果更接近 1D Timoshenko 梁模型(您可以在我们上一篇博客中找到 1D 模拟的结果)。
3D模型
只要没有面外力作用在结构上,并且面内力不沿面外方向变化,2D 建模方法就很有用。对于更一般的载荷条件和结构约束,3D 模型可以提供更准确的信息,但计算量更大。对于真正的 3D 模型,您需要选择 3D 空间维度和固体力学 接口。
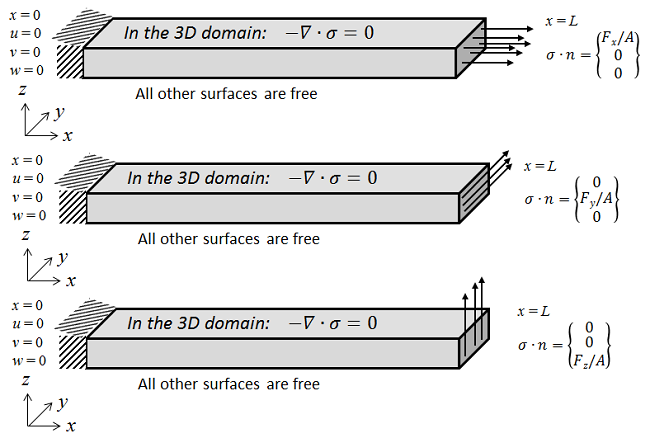
承受轴向和横向载荷的一端固定一端自由的梁的 3D 表示。通过求解这三种载荷下的模型,能够计算轴向和弯曲刚度。
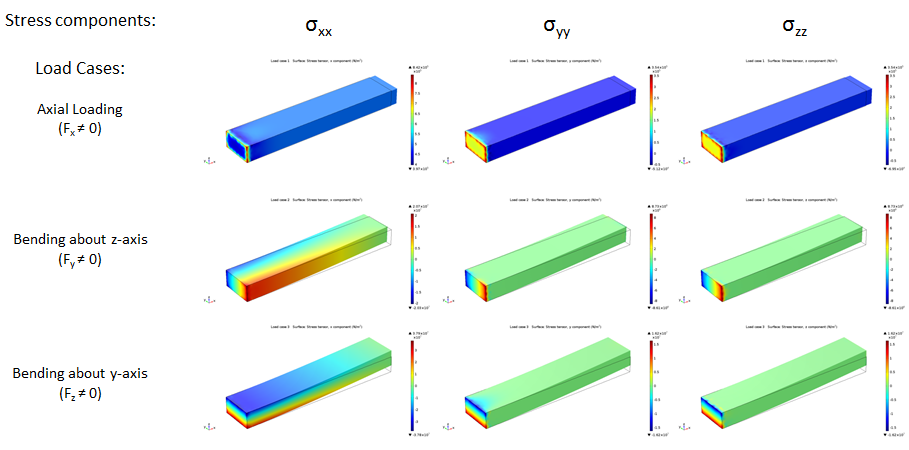
三种载荷工况下的轴向应力汇总。注意固定端的应力集中是由固定约束边界条件和通过泊松效应沿不同方向的应变耦合引起的。
接下来,我们来看看由 3D 模型计算的轴向和弯曲刚度。我们将计算两种情况下的刚度:首先将泊松比设置为 0.3,然后将其设置为 0。这样我们就能够将 3D 结果与 1D 梁理论结果进行比较。
| 泊松比 | kxx[N/m] | kyy[N/m] | kzz[N/m] |
|---|---|---|---|
| ν = 0 | 4×109 | 3.91×107 | 9.94×106 |
| ν = 0.3 | 4.02×109 | 3.92×107 | 1.006×107 |
请注意,当泊松比为 0 时,计算结果与使用 1D Timoshenko 梁理论计算的结果完全匹配。当泊松比为 0.3 时,由于考虑了剪切柔性,Timoshenko 理论了预测较低的弯曲刚度。然而,由于固定约束边界条件,3D 模型预测的轴向和弯曲刚度略高,因此产生了额外的刚度效应,抵消了剪切柔度,尤其是在最小剪切柔度方向弯曲时。
如果我们没有在 3D 中对结构进行建模,就可能会忽略这里看到的真实效应。
刚度还是柔度?
现在,我们来重新审视一下我们计算刚度的方法。
我们固定了梁的一端,并在另一端施加一个力。一次改变该力矢量的一个分量,使其非零(并保持其他力分量为零),并计算由此产生的梁的平均尖端位移。 在这些条件下,力矢量(F) 和位移矢量 (u) 应该严格使用柔度矩阵 [s] 进行关联,这样就可以得到 \bold{u}=[s]\bold{F}。
同样的等式也可以写成矩阵形式:
式中,柔度分量 sij 表示与当沿第 jth 个方向(j 可以是 x、y、z)施加增量力时在第 ith 个方向(i 可以是 x、y、z)获得的增量位移相关的线性柔度。我们将这种方法称为力控制法。
基于我们之前对刚度的定义,现在可以定义一个广义刚度矩阵,使得 \bold{F} = [k] \bold{u}。
我们也可以用矩阵公式表示:
在刚度矩阵中,对角线项表示轴向和弯曲刚度,非对角线项表示由于拉伸-弯曲耦合引起的任何刚度。在没有这种拉伸-弯曲耦合的情况下(如本文的示例),会得到一个对角线柔度矩阵。因此,我们可以说 kxx = 1/sxx, kyy = 1/syy, 和 kzz = 1/szz。这是我们目前所使用的。
请注意,第二个矩阵公式的输入等于位移的不同分量,而我们感兴趣的输出等于在具有指定位移的边界处“感觉到”的反作用力的分量。因此,为了找到刚度矩阵的不同分量,我们需要一次改变位移矢量的一个分量,使其不为零(并将其他位移分量设置为零),并计算产生的反作用力。
我们施加轴向和横向载荷的 “自由端”不再自由。基于此,我们现在可以说刚度分量 kij 表示与当沿第 j 个方向(j 可以是 x、y、z)施加一个增量位移时在第 i 个方向(i 可以是 x、y、z)获得的增量反作用力相关的线性刚度。我们将这种方法称为位移控制法。
还能有其他刚度吗?
到目前为止,我们的讨论仅限于使用力和位移获得的轴向和弯曲刚度。然而,实际上,在空间中的任何一点,一个结构都可以有 6 个自由度,其中 3 个对应平移,另外三个对应旋转。类似地,不仅是在与 x 轴,y 轴或 z 轴平行的一个方向的边界上施加力,也可以围绕这 3 个轴施加力矩。
对于像我们示例中的悬臂梁,关于 x 轴会产生扭转,关于 y 轴和 z 轴会产生弯曲。所有这些信息都可以使用以下矩阵公式表示:
这表明,我们可以有一个广义的 6×6 刚度矩阵,它可以容纳多种类型的刚度项,例如轴向、剪切、弯曲和扭转,以及这些模式之间的耦合项。
在 COMSOL Multiphysics 中计算刚度:替代方法
有了新的信息,让我们再重新审视下我们的梁模型:

在 3D 中定义的梁模型显示了如何指定梁尖端的位移。
为了在 COMSOL Multiphysics 中实施位移控制法,我们需要进行以下操作:
- 找到一种方法来指定 x = L 处梁边界上的位移
- 求 x = L 处梁边界上的反作用力
指定位移
如果我们使用梁理论模型(用于 1D 分析),就能够明确地处理所有 6 个自由度(位移和旋转)。因此,我们可以用指定的位移/旋转替换点载荷,将位移设置为某个非零值(比如 1mm),同时不对梁尖端的旋转施加任何约束。
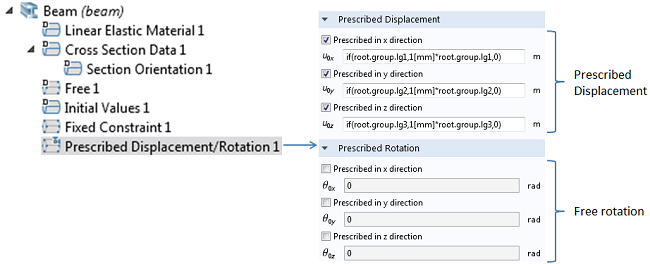
施加于 1D 梁尖端的指定位移/旋转特征。允许自由旋转。
如上一篇博客所示,我们可以使用 if() 算子和与载荷组关联的名称(例如 root.group.lg1),这样就能在为多个载荷工况求解同一模型时,一次只能使位移矢量的一个分量非零。

显示如何设置三个载荷工况,并且一次仅使用一个活载荷组求解模型的屏幕快照。
当使用固体力学模型(2D 和 3D)时,我们只能指定或计算三个平移自由度(位移),这些自由度反过来又可以用于计算旋转。这也意味着当我们设置一个位移控制的刚度计算时,使用梁理论可以轻松地在一个点上约束旋转或允许自由旋转。
另一方面,在固体力学模型中,不可能通过将旋转与位移解耦来自由地指定或约束该表面上任何位置的旋转,这是因为我们正在处理的是边界上位移的空间变化。这意味着如果我们简单地分配一组指定的横向位移(比如 u= 0,v= 1 mm 和 w= 0),它将完全约束旋转(即 ΦX=Φy=Φz= 0), 从而增加梁的有效抗弯刚度。这时候,我们就可以使用 COMSOL 软件的刚性连接件边界条件 ,它可以帮助我们解决 2D 和 3D 实体模型中的问题。
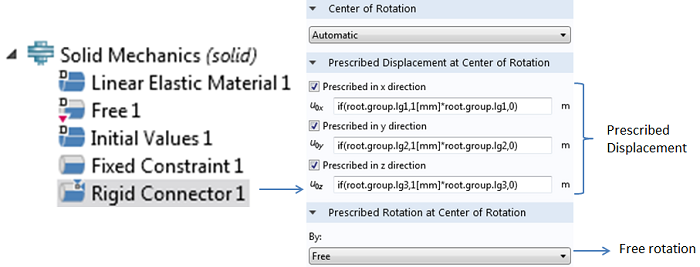
应用在 3D 梁边界上的刚性连接件特征。在边界的质心处允许自由旋转。
在我们的模型中,我们可以使用与之前类似的表达式来指定刚性连接件边界条件中的位移,以使用载荷组和载荷工况一次改变一个位移分量。刚性连接件将在梁的另一端引入与固定约束相同类型的局部刚度和应力干扰。
计算反作用力和刚度
可以通过设置积分耦合算子来计算反作用力,该算子可用于对边界上所有节点的反作用力求和。COMSOL Multiphysics 提供了一些例如 solid.RFx, solid.RFy, 和 solid.RFz 的预定义变量,使我们可以访问反作用力。然后可以将刚度计算为总反作用力与梁末端指定位移值的比值。或者,如果梁具有拉伸-弯曲耦合,则使用梁尖端位移的平均值可能很有用。在这种情况下,垂直于载荷应用方向的平均位移将不为零。
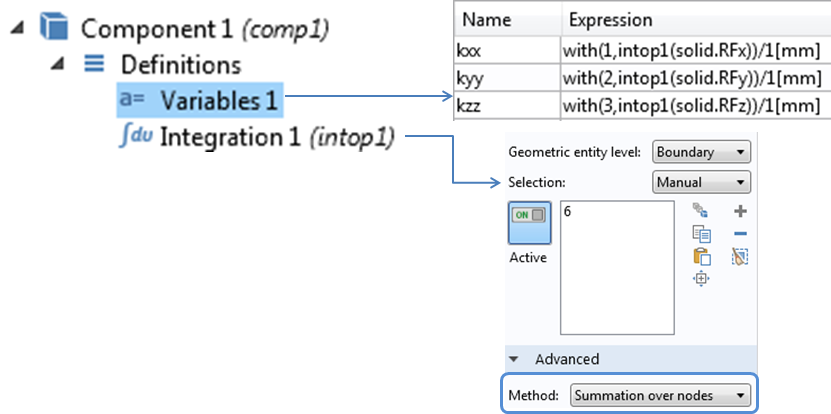
积分耦合算子和为计算刚度定义的变量的屏幕截图。
轴向和弯曲刚度总结
最后,我们对通过忽略或包括泊松效应和剪切效应在不同空间维度中计算的所有轴向和横向刚度值进行了总结。使用力控制 和位移控制方法 获得的刚度值结果非常一致,因此可以进行一致性检查:
| 空间维度(泊松比) | kxx[N/m] | kyy[N/m] | kzz[N/m] |
|---|---|---|---|
| 1D Timoshenko(ν=0) | 4×109 | 4×107 | 1×107 |
| 1D Timoshenko(ν=0.3) | 4×109 | 3.91×107 | 9.94×106 |
| 1D Timoshenko(ν=0.3) | 4×109 | 3.88×107 | 9.92×106 |
| 2D 平面应力(ν=0) | 4×109 | 3.91×107 | 9.94×106 |
| 2D 平面应力(ν=0.3) | 4.02×109 | 3.89×107 | 9.94×106 |
| 3D (ν=0) | 4×109 | 3.91×107 | 9.94×106 |
| 3D (ν=0.3) | 4.04×109 | 3.92×107 | 1.01×107 |
结论
在这篇博客中,我们更加详细地探讨了结构的轴向和弯曲刚度的概念。我们从适用于 0D 模型的传统刚度定义开始,然后将其扩展到适用于包含多轴载荷的 1D、2D 和 3D 模型结构的假设和理论。我们看到,结构的刚度很少可以用单值数来表示。
结构刚度可能会受到我们未在此处探讨的其他几个因素的影响,包括:
- 几何非线性:
- 当刚度成为力或位移大小的函数时会发生什么?
- 材料非线性:
- 我们如何定义材料的刚度,例如高于屈服强度的金属或不遵循胡克定律的橡胶?
- 多物理场:
- 当非机械载荷(例如热载荷或流体载荷)产生结构位移时,我们如何定义刚度?
下一步
- 阅读本系列的上一篇博客: 线弹性结构刚度的计算:第 1 部分
- 如果您对使用 COMSOL Multiphysics 计算刚度有任何疑问, 请联系我们



评论 (0)