声学与振动 博客文章
在 COMSOL® 中计算瞬态声压级
2022年 9月 13日
当尝试使瞬态仿真的结果在对数尺度上更容易解释时，了解声压级指标很重要。阅读本文，了解如何计算这些指标中的 3 个。
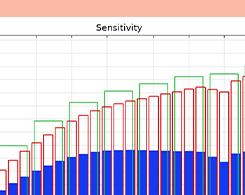
用于声学仿真的倍频带图
2022年 9月 9日
倍频带图提供了一种简单而灵活的方式，用于表示声学分析中的任何频率响应、传递函数、灵敏度曲线、传输损耗或插入损耗。
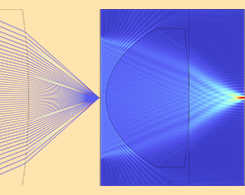
如何使用空间快速傅里叶变换（FFT）进行光学应用仿真
2022年 8月 19日
COMSOL Multiphysics® 6.0 版本包括新的空间 FFT 特征。了解如何在光学应用中应用该功能。
设计对海洋生物安全的潮汐涡轮机
2022年 7月 18日
一位来自 Xi Engineering 公司的特邀博主讨论了他的组织如何使用声学仿真来研究潮汐涡轮机对海洋物种的影响。
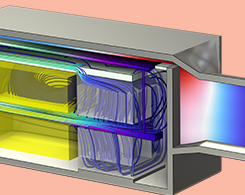
使用哪种耦合特征对扬声器驱动器进行建模？
2022年 4月 26日
探索如何模拟 4 种不同的扬声器驱动器，包括动圈换能器，平衡电枢接收器，压电驱动器和静电驱动器。
使用间断伽辽金法模拟压电效应
2022年 2月 9日
COMSOL Multiphysics® 软件 6.0 版本新增了一项功能，可以方便地对涉及使用压电器件的应用进行建模。查看如何将其添加到您的模型中。
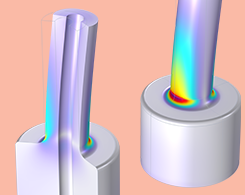
通过二维轴对称建模分析扭转问题
2022年 2月 8日
从 6.0 版开始，您可以使用固体力学接口轻松地将圆周位移包含在二维轴对称模型中。 在这里查看一个示例。
室内音乐厅声学射线追踪仿真与验证
2022年 1月 11日
著名的柏林音乐厅剧院拥有 3 个独立的大厅：大礼堂、小礼堂和现代的维尔纳奥托礼堂。 在这里，我们通过仿真探索小礼堂的声学效果。