Menu
COMSOL 博客

介电泳分离

Author Image
作者 Bjorn Sjodin
2015年 1月 23日

如何用电场控制电中性粒子的运动？这听起来似乎是不可能的，但在这篇文章中，您会看到介电泳（DEP）现象可以解决这个难题。我们将学习如何利用介电泳进行颗粒分离，并演示一个简单的生物医学仿真 App，该 App 是使用 App 开发器创建的，通过 COMSOL Server™ 运行。

在非均匀静电场中粒子所受的力

在直流和交流场中，都会发生介电泳效应。我们先来看看直流的情况。

考虑一个浸入流体中的介电粒子。另外，假设存在一个施加到流体-颗粒系统的外部静态(DC)电场。在这种情况下，只要粒子的介电常数高于周围流体的介电常数，粒子就会从弱电场区域被拉到强电场区域。如果粒子的介电常数低于周围流体，那么情况正好相反，粒子会被拉到弱电场区域。这些效应分别被称为正介电泳 (pDEP)和负介电泳 (nDEP)。

下面两幅图片分别演示了这两种情况，并将几个重要的量可视化：

  • 电场
  • 麦克斯韦应力张量（表面力密度）

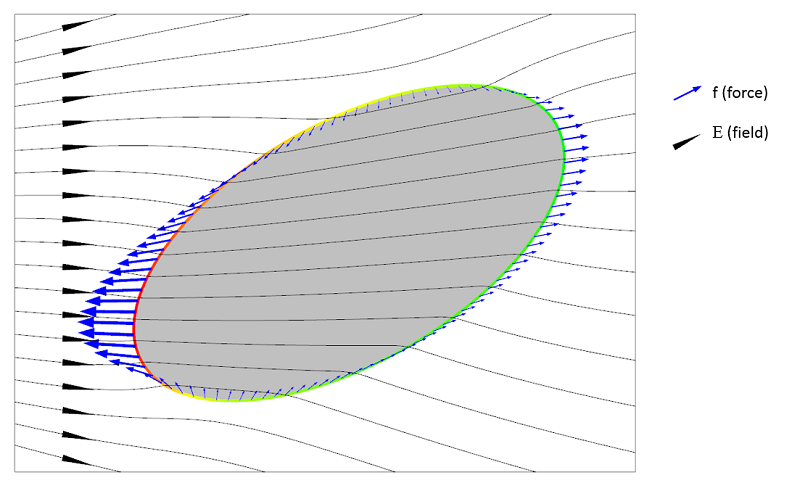
正介电泳示意图。
正介电泳(pDEP)的示意图，粒子介电常数高于周围流体的介电常数 \epsilon_p > \epsilon_f。

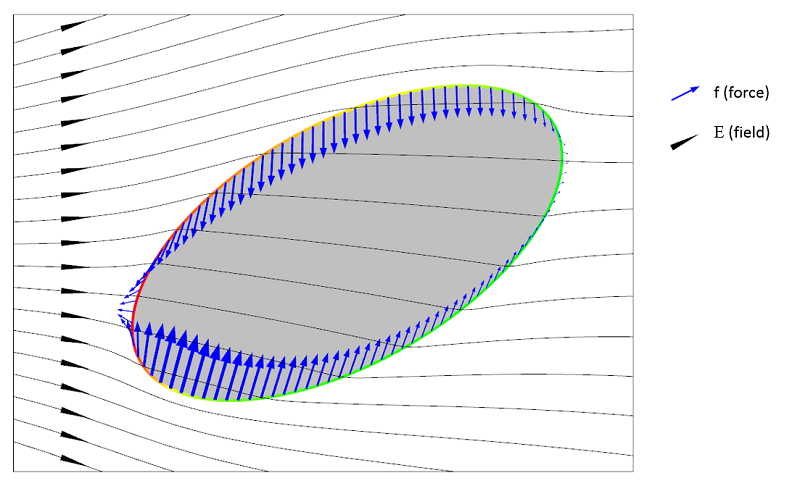
负介电泳示意图。
负介电泳(nDEP)的示意图，粒子介电常数低于周围流体的介电常数 \epsilon_p < \epsilon_f。

麦克斯韦应力张量代表粒子表面的局部力场。为了使这个应力张量能够代表作用在粒子上的力，流体需要是“简单的”，也就是它不应该表现出太复杂的机械行为。假设流体是简单的，我们可以从上面的插图中看到，在 pDEP 和 nDEP 这两种情况下，粒子上的净力看起来是方向相反的。对表面力进行积分确实会出现这种情况。

事实证明，如果我们把粒子缩小，例如一个无限小的情况，一个非常小的粒子在流体中像偶极子一样运动，那么净力是电场平方梯度的函数。

为什么净力会有这样的表现？为了理解这一点，我们来观察在粒子表面的一个点上会发生什么。在这样一个点上，电表面力密度的大小 f，是电荷乘以电场的函数。

(1)

f \propto \rho E

其中，\rho 是感应极化电荷。(让我们暂时忽略一些量是向量，只看量级和比例关系，做一个纯粹的现象学论证。)

感应极化电荷与电场成正比：

(2)

\rho \propto \epsilon E

联立两个公式，得到：

(3)

f \propto \rho E = \epsilon E^2

但这只是表面某一点上的局部表面力密度。为了从表面上各点的所有这些表面力贡献中得到净力，粒子的一侧和另一侧之间需要存在力的大小差异。这就是净力 \bf{F}，与电场模的平方梯度成正比的原因。

(4)

\mathbf{F}
\propto \epsilon \nabla |\mathbf{E}|^2

在上述推导中，我们走了一些捷径。例如，在这种关系中，介电常数是什么？是粒子的还是液体的，或者与两者都不同？粒子的形状如何？是否有形状因子？

现在，让我们来解决其中的一些问题。

作用在球形粒子上的力

在更严格的推导中，我们改用电偶极子上力的矢量值关系：

(5)

\mathbf{F} = \mathbf{P} \cdot \nabla \mathbf{E}

其中，\bf{P} 是粒子的电偶极矩。

为了获得不同粒子的力，我们只需插入电偶极矩的各种表达式。在这个表达式中，我们还可以看到，如果电场是均匀的，就不会得到任何力(因为粒子很小，它的偶极矩被认为是一个常数)。对于在电场中半径 r_p 很小的球形介电粒子，其偶极矩为：

(6)

\mathbf{P}= 4 \pi r_p^3 k \mathbf{E}

其中，k 是取决于粒子和周围流体的介电常数的参数。该因子 4 \pi r_p^3 可以被视为形状因子。

结合这些，得到：

(7)

\mathbf{F} = 4 \pi r_p^3 k \mathbf{E}
\cdot \nabla\mathbf{E} = 2 \pi r_p^3 k \nabla |\mathbf{E}|^2

这再次表明，粒子所受的力对电场模的平方梯度的依赖性。

在时变电场中粒子所受的力

如果电场是时变的(交流电)，情况会稍微复杂一些。我们还假设存在由电导率 \sigma 表示的损耗。球形粒子上的介电泳净力 \bf{F} 为 ：

(8)

\mathbf{F}
= 2 \pi r^3_p k \nabla |\mathbf{E}_{\textrm{rms}}|^2

其中

(9)

k = \epsilon_0 \Re\{ \epsilon_f \} \Re \left\{ \frac{\epsilon_p -\epsilon_f}{\epsilon_p + 2 \epsilon_f} \right\}

和

(10)

\epsilon = \epsilon_{\textrm{real}} -j \frac{\sigma}{2 \pi \nu}

是复值介电常数。下标 p 和 f 分别表示粒子和流体。粒子的半径是 r_p，\bf{E}_{\textrm{rms}} 是电场的均方根。交流电场的频率为 \nu。

从这个表达式中，我们可以通过设置 \sigma = 0 来获得静电情况下的力。（不能采取频率变为零时的极限情况，因为电导率在静电学中没有意义。）

在介电泳力的表达式中，我们可以看到流体和粒子之间的介电常数差异确实起到了重要作用。如果这个差异的符号切换，那么力的方向就相反。涉及介电常数值的求差与求和运算的因子 k 称为复数 Clausius-Mossotti 函数，您可以点击此处阅读更多相关信息。这个函数对介电泳力的频率依赖性进行了编码。

如果粒子不是球形的，而是椭圆形的，那么使用另一个比例因子。对于具有一个或多个薄外壳且有不同介电常数值的粒子，例如生物细胞，也有众所周知的介电泳力表达式。下面介绍的仿真 App 包括细胞膜的介电常数，它被表示为一个壳。

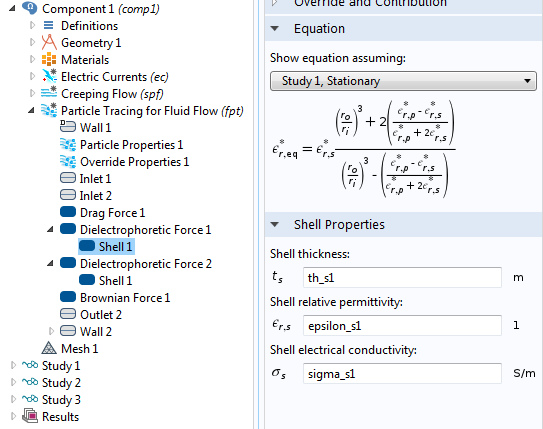
设置窗口显示一个介电壳有效介电常数。
介电壳的有效介电常数的设置窗口。

可能还有其他作用在粒子上的力，如流体曳力、重力、布朗运动力和静电力。下面显示的仿真 App 包括曳力、布朗运动和介电泳力的贡献。在粒子追踪模块中，我们无需输入冗长的力表达式，一系列可能的粒子力都已经在软件中内置。下图显示了流体流动的粒子追踪 接口中可用的力。。

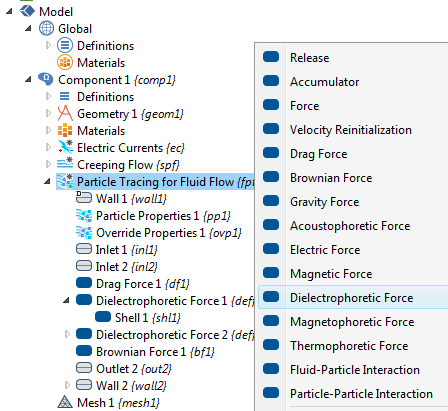
屏幕截图高亮显示了不同粒子力选项。
流体流动的颗粒追踪接口中不同的粒子力选项。

颗粒的介电泳分离

用于智能手机的医疗分析和诊断类应用将快速增长。我们可以想象，在未来智能手机能与一个可以采样和分析血液的硬件结合起来使用。

假设这样一个案例，对其进行分析可以分为三个步骤：

  1. 使用直接连接到智能手机的硬件提取血液，并计算平均血小板和红细胞直径。
  2. 计算红细胞和血小板的分离效率。这种效率需要很高，以便对分离的红细胞进行进一步诊断。
  3. 使用计算出的最佳分离条件，用连接到智能手机上的硬件分离红细胞。

COMSOL Multiphysics 仿真 App 的重点是上述整个分析过程的第 2 步。通过利用血小板是血液中最小的细胞，并且具有与红细胞不同的介电常数和电导率这一事实，可以使用介电泳进行基于尺寸的血液分离；换句话说，就是可以将红细胞与血小板分离。

红细胞是最常见的血细胞类型，也是脊椎动物机体通过循环系统的血流向身体组织输送氧气（O2）的主要手段。血小板，也称为凝血细胞，是具有止血功能的血细胞。

我们使用 App 开发器，创建了一个仿真 App，该 App 使用流体流动颗粒追踪 接口中提供的介电泳力 功能演示了血小板与红细胞（RBC）的连续分离。(创建该仿真 App 还需要以下其中一种模块：CFD 模块、微流体模块或地下水流模块以及 MEMS 模块或 AC/DC 模块。)

该仿真 App 是基于 N. Piacentini 等人在 Biomicrofluidics(vol. 5, 034122, 2011)上发表的论文 “Separation of platelets from other blood cells in continuous-flow by dielectrophoresis field-flow-fractionation”中详细描述的片上实验室（LOC）装置建立的。

该装置由两个入口、两个出口和一个分离区组成。在分离区中，有一个控制粒子轨迹的极性交替电极排列。电极产生了利用介电泳效应所需的非均匀电场。下图是该模型的几何形状。

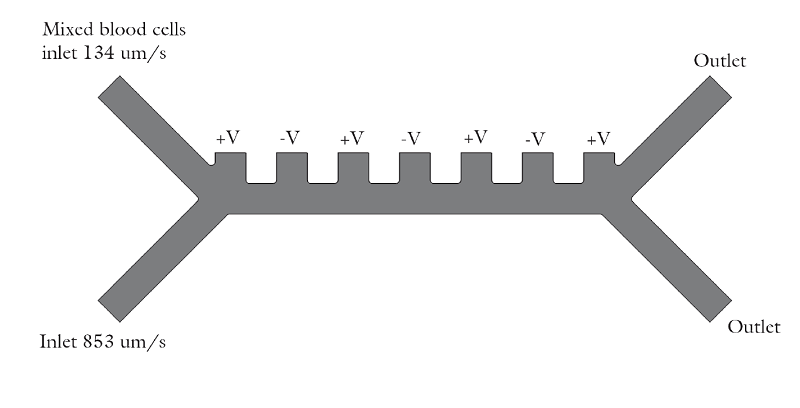
颗粒分离仿真App中使用的几何图形示意图。
颗粒分离仿真 App 中使用的几何图形。

下部入口的入口速度（853μm/s）明显高于上部入口速度（154μm/s），以便将所有注入的颗粒集中于上部出口。

该仿真 App 基于使用以下物理场接口的模型构建：

  1. 蠕动流(微流体模块)用于模拟流体流动。
  2. 电流 (AC/DC 或 MEMS 模块)用于模拟微通道中的电场。
  3. 流体流动颗粒追踪(粒子追踪模块)，用于计算红细胞和血小板在阻力和介电泳力的影响下以及布朗运动下的轨迹。

底层模型中使用了三个研究：

  1. 研究 1 求解了频率为 100kHz 的稳态流体动力学和频域(AC)电势。
  2. 研究 2 使用瞬态研究步骤，该步骤利用研究 1 中的解并在没有介电泳力的情况下计算粒子轨迹。在这项研究中，所有颗粒(血小板和红细胞)都被集中到同一个出口。
  3. 研究 3 是第二个瞬态研究，包括介电泳力的影响。

您可以在此处下载该 APP 所基于的模型。

生物医学仿真 App

为了创建仿真 App，我们使用了适用于 Windows® 操作系统的 COMSOL Multiphysics® 5.0 版本中的 App 开发器。

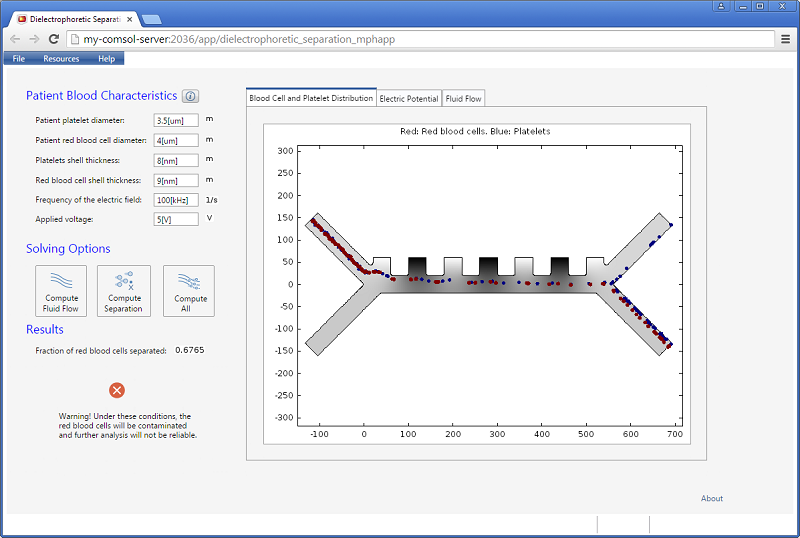
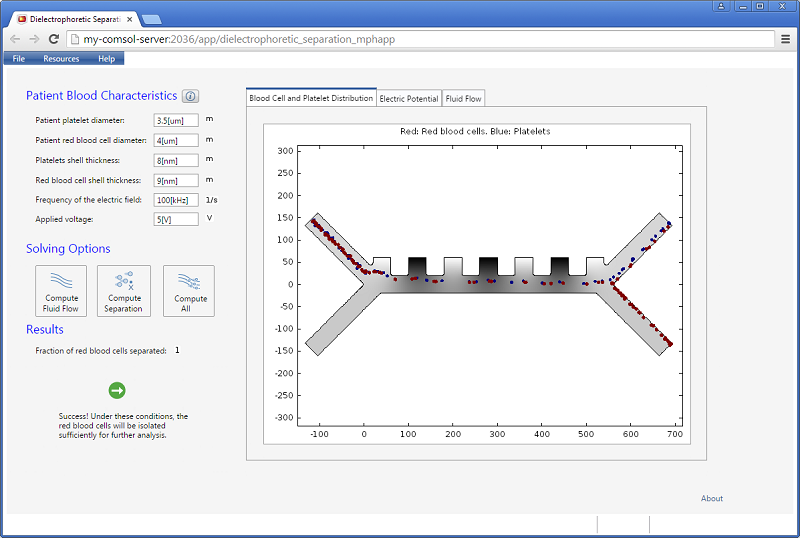
下图显示了应用首次启动时仿真 App 的外观。在本例中，我们已连接到 COMSOL Server™ 安装，这样就能在标准网页浏览器中运行 COMSOL Multiphysics 应用程序。

生物医学仿真App
在标准网页浏览器中运行的生物医学仿真 App。

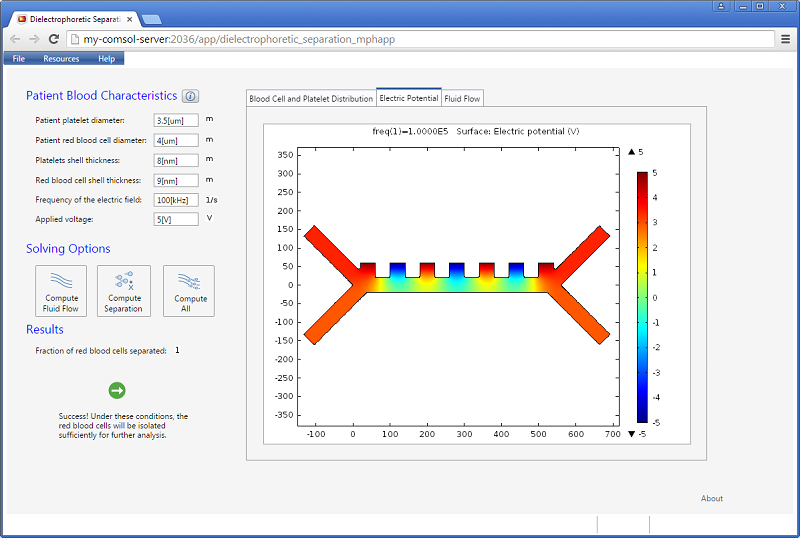
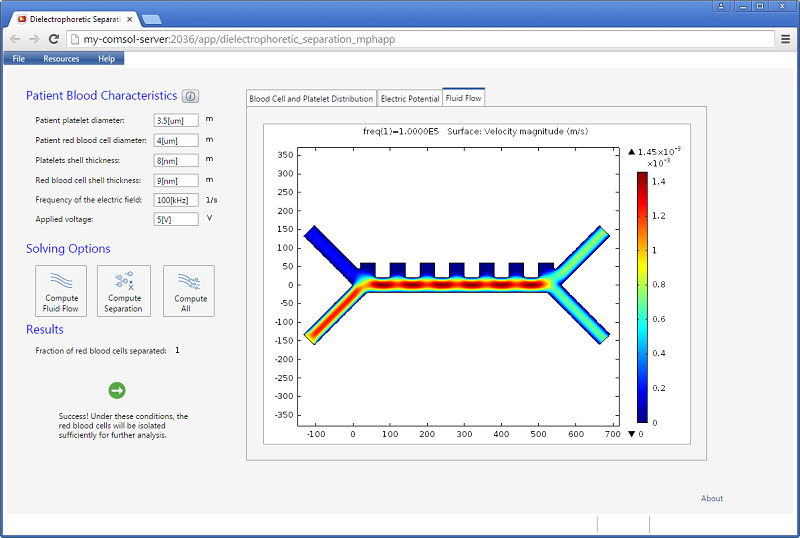
该仿真 App 允许用户输入一些量，例如电场的频率和施加的电压。结果包括一个分离的红细胞比例的标量值。此外，在选项卡窗口中提供了三种不同的可视化效果：血细胞和血小板分布、电势和流体流动的速度场。

下图显示了电势和流场的可视化结果。

屏幕截图显示了微流体通道中的瞬时电势。
屏幕截图显示了微流体通道中的瞬时电势。

流体速度大小
屏幕截图显示了流体速度大小。

该仿真 App 有三种不同的求解选项，分别用于仅计算流场、仅使用现有流场计算分离或将两者结合起来。如果没有分离干净，系统会显示一条警告消息。

增加施加的电压将增加介电泳力的大小。如果分离效率不够高，我们可以增加电压并点击全部计算 按钮，因为在这种情况下，场和粒子的轨迹都需要重新计算。我们可以通过改变频率来控制介电泳力表达式的 Clausius-Mossotti 函数值。事实证明，在 100kHz 的指定频率下，只有红细胞会从下部出口出来。

在这种情况下，流体的介电常数比颗粒的介电常数高，血小板和红细胞都承受了负的介电泳力，但大小不同。为了获得成功的整体设计，我们需要平衡介电泳力相对于流体曳力和布朗运动力。下图显示了一个使用输入参数的模拟，这些参数通过下部出口分离出红细胞的成功率为 100%。

屏幕截图显示了红细胞的成功分离。
成功分离红细胞。

扩展阅读

如果您要了解有关介电泳及其应用的更多信息，请单击下面列表中的链接。列表中包含一个指向 App 开发器视频的链接，该视频还向您演示了如何使用 COMSOL Server™ 部署仿真 App。

Windows 是微软公司在美国和/或其他国家/地区的注册商标或商标。

博客分类

相关主题

评论 (0)

正在加载...
浏览 COMSOL 博客
类别
标记