
我们在之前的博客中已经介绍了怎么利用对称、反对称,以及周期性边界条件来节省电磁模型的建模时间。今天,我们将为您展示一个利用轴对称建立的模型 — 锥型喇叭天线模型。
利用二维轴对称节省建模时间
尽管我们能够建立并求解三维的锥型喇叭天线模型,但是这类模型需要调用大量的计算资源来进行求解。利用结构的对称性,我们可以非常快速地求解电磁场问题。因为我们处理的几何是一个圆锥,模型在结构上关于轴对称,所以可以采用二维轴对称来简化建模。
尽管结构上轴对称,但是电磁场在绕轴的方位角上会有一些不同,所以电磁场具有方位角变量。RF模块和波动光学模块可以用来对于具有不同方位角模式数的轴对称结构进行建模。
我们可以利用上述功能;通过创建一个二维轴对称模型,求解多个不同的方位角模式数,从而可以创建一个相比完整三维模型的计算速度要快,但内存占用要少的模型。
喇叭天线的一般注意事项
喇叭天线可以根据整体造型以及内部构造分为各种样式。这些属性决定了天线的波束轮廓,带宽以及交叉极化。
交叉极化是指电磁场的极化方向与期望的方向相反。例如,我们想要电磁场在垂直方向极化,结果却在水平方向极化。
天线的漏斗状部分与波导相连,将电磁波传递给天线。喇叭的形状将决定其适用于什么应用。例如,扇形喇叭(下图 b 和 c)的典型应用是全搜索雷达天线。
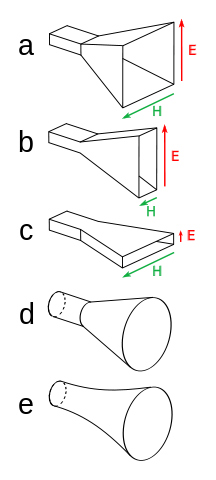
各种喇叭天线的形状:a) 金字塔型;b) 扇形,E-面;c) 扇形,H-面;d) 圆锥形;e) 指数型。 “喇叭天线类型” 图片为 Chetvorno 制作,已获得 Creative Commons Zero 授权,并通过 Wikimedia Commons分享。
波纹状锥型喇叭天线模型
在我们例子中的天线形状为锥型(如上图 d),天线内部的表面具有波纹;波纹状锥型喇叭天线通过波导馈给。波导传递 TE 模式的电磁波通过波纹漏斗,结果产生 TM 模式的电磁波。由于在整个圆锥中都有波纹表面,所以不同的模式被混合在一起,相比于最初的激励TE模式,孔隙处交叉极化更低。
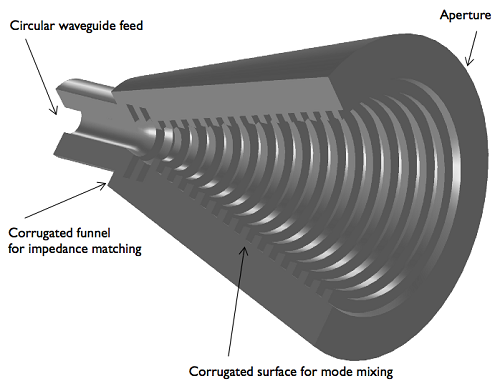
锥型喇叭天线:基于二维轴对称模型建立的三维几何视图。波导以 TE1m 模式馈给天线 (m = ±1), 当其通过天线的时候与 TM1m 模式混合。
前文提及了交叉极化,但是为什么我们要减少交叉极化的发生呢?如果有大量的交叉极化发生,而附近的其他信道具有交替的垂直和水平极化的话,那么我们的信号就可能与附近的其他信道相干扰。这不是我们想要的。
研究喇叭天线中的交叉极化
为了研究交叉极化,我们可以使用 COMSOL Multiphysics 及其 RF 模块来建立模型。就如前面提到的,我们可以使用二维轴对称模型代替三维模型,从而节省计算时间。我们使用电磁波,频域接口来创建模型。
我们将跳过创建模型的步骤,而是直接来分析结果。如果您想要复现下图的结果,可以从案例库中下载模型文档和 MPH 文件。
首先,我们可以看到天线的定向波束图是:
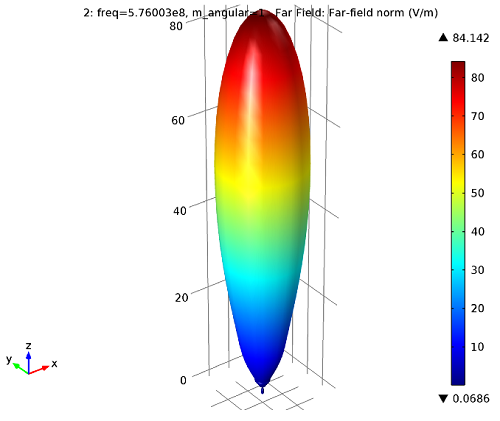
远场图:天线的定向波束图
接下来,我们可以分析天线入口和出口处的电场。通过求解 m = +1 和 m = -1 时的模型,我们得以比较出口处 x 和 y 方向上的线性极化。
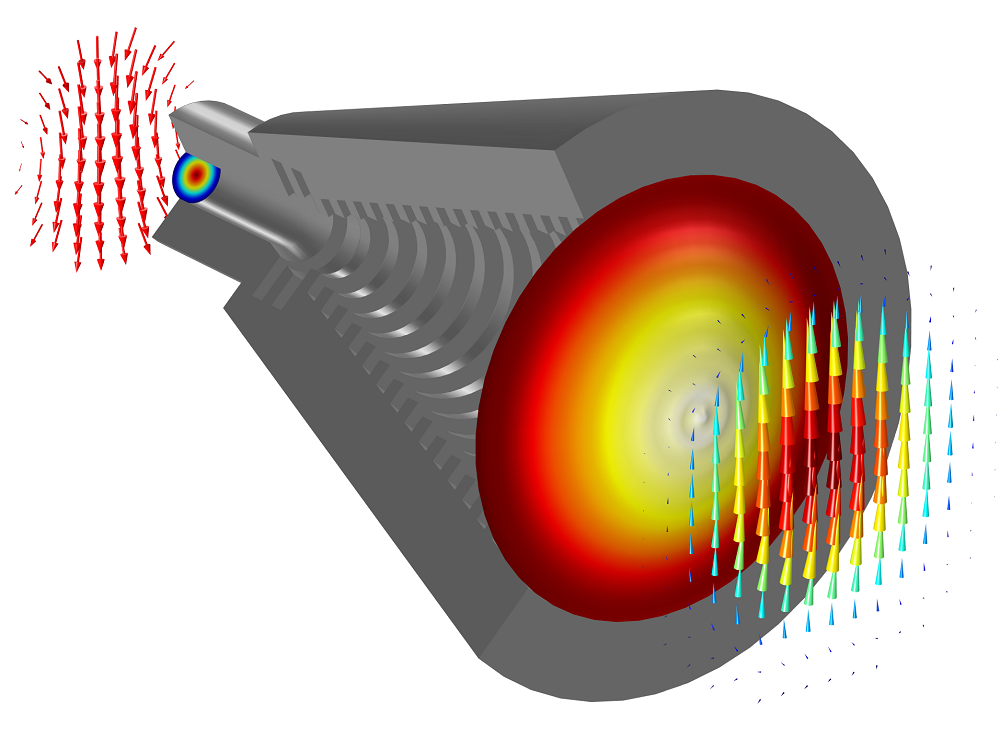
m = +1和m = -1 的线性叠加,在天线入口和出口处的电场。
对于波导的馈给,场主要是沿 x 方向,但不是线性极化。在孔隙处,场几乎完全线性极化。为了量化两个方向上的极化,我们可以计算锥型喇叭天线入口和出口位置各个电场分量绝对值的积分。计算之后我们得到,在入口处比例大约为 5:1,而在出口处比例大概为 40:1。换句话说,我们减少了 8 倍的交叉极化。



评论 (0)