材料模型 博客文章

模拟线弹性材料能有多难?
2015年 6月 29日
线弹性模型是结构力学分析中最基础的材料模型。虽然听上去微不足道,但模型中却包含不少难以一眼看出的重要细节。在本篇博客文章中,我们将深入讨论线弹性材料模型的相关理论和应用,并且大致介绍其各向同性和各向异性、材料数据的容许值、不可压缩性,以及与几何非线性之间的相互作用。

将测量数据拟合至各种超弹性材料模型
2015年 6月 24日
想要将你的实验数据拟合到不同的超弹性材料模型中?借助 COMSOL Multiphysics 中的优化接口,您可以将一条曲线拟合到多个数据集。
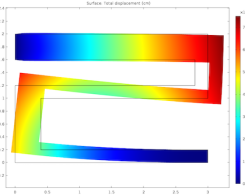
如何建立吸湿膨胀模型
2015年 6月 9日
从木材建筑和纸张到电子和食品加工,吸湿膨胀发生在各个工业领域。了解如何在COMSOL Multiphysics®中为这种现象建模。

有限元模型中的奇点:如何处理模型中的红点
2015年 6月 3日
你的模型中是否显示出红点?探索有限元模型中奇点的常见原因,何时、如何消除它们,以及如何解释您的仿真结果。

从测量中获取结构力学的材料数据(第二部分)
2015年 5月 5日
在本系列的第一篇博客中,我们讨论了将测量材料数据转化为本构模型时的一些注意事项;并详细介绍了超弹性材料。今天,我们将讨论如何使用非线性弹性和弹塑性材料,并将介绍一种您可以直接在 COMSOL Multiphysics 中使用您的测量数据的方法。

从测量中获取结构力学的材料数据
2015年 2月 23日
我们经常碰到这类问题:“能否直接在 COMSOL Multiphysics 中输入测量得到的应力-应变曲线。”在这个新的博客系列中,我们将详细介绍如何处理及解读从测试中获取的材料数据;还将解释为什么简单输入应力-应变曲线的做法并不可取。

非线性弹性材料简介
2015年 1月 9日
非线性弹性材料模型的例子:Ramberg-Osgood, Duncan-Chang, Hardin-Drnevich, Power law 等。文中讨论了如何在你的分析中应用非线性弹性材料。

降低粘弹性结构阻尼器中的振动
2014年 8月 20日
进行结构设计时,特别需要关注会暴露在地震或风致振动风险下的区域。一般会在结构布局中加入粘弹性结构阻尼器来限制应变,降低建筑物在此类激励下的崩塌风险。
