
在之前的博客中,我们向大家介绍了什么是吸湿膨胀,并描述了它对特定类型材料的影响。使用 COMSOL Multiphysics 软件中的吸湿膨胀 功能,可以对这种重要的效应进行建模。这篇博客,我们将带您完成这个建模过程,并着重介绍 COMSOL 5.1 版本中新增的多物理场耦合功能。
吸湿膨胀效应概述
首先,我们来快速复习一下吸湿膨胀效应的概念。当固体进入一个潮湿的环境时,其中一部分固体有可能会吸收水分子。吸收和储存水分子会导致固体膨胀,并使其面临更大的应力和应变。这种效应被称为吸湿膨胀。
从木材建筑、造纸到电子和食品加工行业,吸湿膨胀现象存在于各个工业领域中。无论这种现象是预期的行为还是不良的影响,为了量化它所产生的影响,必须对它进行准确地建模。
COMSOL Multiphysics 中的吸湿膨胀功能可以帮助您实现这一点。作为结构力学接口中大多数材料模型的子节点,该功能使您能够分析固体内水分集中产生的影响,例如产生的变形和应力。
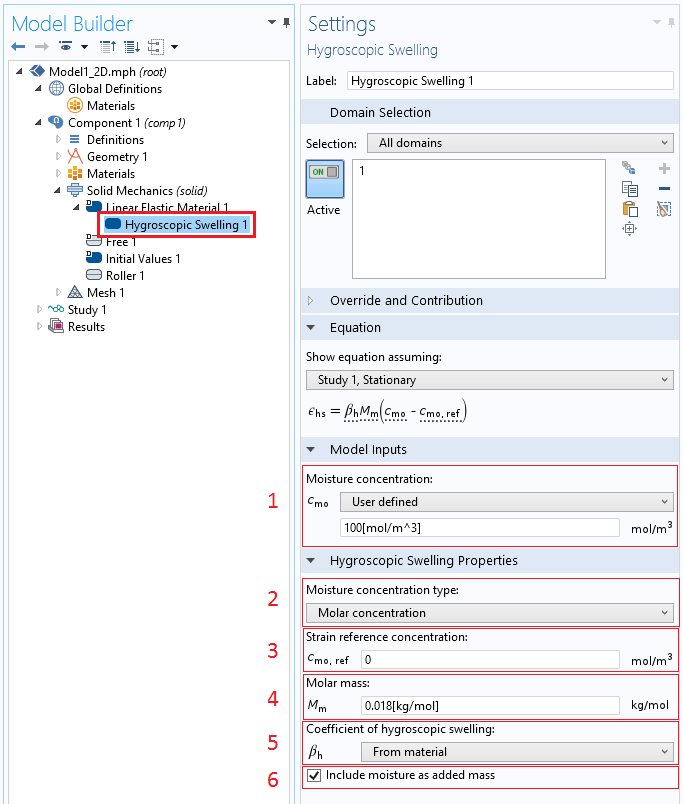
吸湿膨胀功能的用户界面(UI)。主要的输入用颜色和数字表示。
根据上图的引导,现在我们来仔细看看如何使用这个功能。
理解吸湿膨胀
吸湿膨胀会产生非弹性应变,该应变与浓度和无应变参考浓度之间的差异成正比:
其中,吸湿膨胀系数 \beta_\textrm{h},可以从材料属性获取,也可以直接从节点中获取(上面屏幕截图中的数字 5)。它不一定是常数;它可以取决于其他变量,例如温度或水分浓度本身。
在小变形理论中,吸湿膨胀的贡献是叠加的,也就是说,非弹性应变是其他非弹性应变和吸湿应变的总和。吸湿膨胀系数是一个二阶张量,可以被定义为各向同性、对角线或对称性。因此,在不同的方向上,膨胀可以是不同的。在木材中,这种影响是非常明显的。
在超弹性材料模型下的大变形理论中,吸湿贡献是倍增的,也就是说,总变形梯度张量 F 是通过吸湿拉伸和缩放的,用于形成弹性变形梯度张量 F_\textrm{e} :
\epsilon=\frac{1}{2} \left( F_\textrm{e}^\textrm{T}F_\textrm{e}-I \right) & F_\textrm{e}=F J_\textrm{hs}^{-1/3}
\\
J_\textrm{hs}= \left(1+\beta_\textrm{h} C_\textrm{diff} \right)^3
\end{array}
在这个例子中,吸湿膨胀系数是各向同性的,所以只考虑了均匀的体积膨胀。
吸湿膨胀有两种类型的影响。当发生在自由结构中时,它会诱发变形。当发生在受约束的结构时,不会发生变形,但会导致结构内部的应力增加。在实际结构中(通常是部分约束),会产生这两种行为的混合影响。
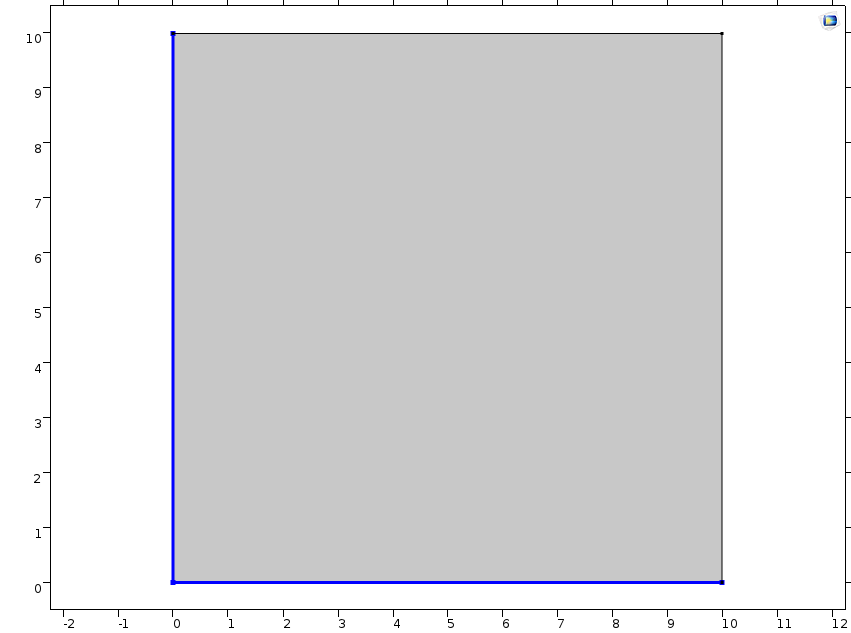
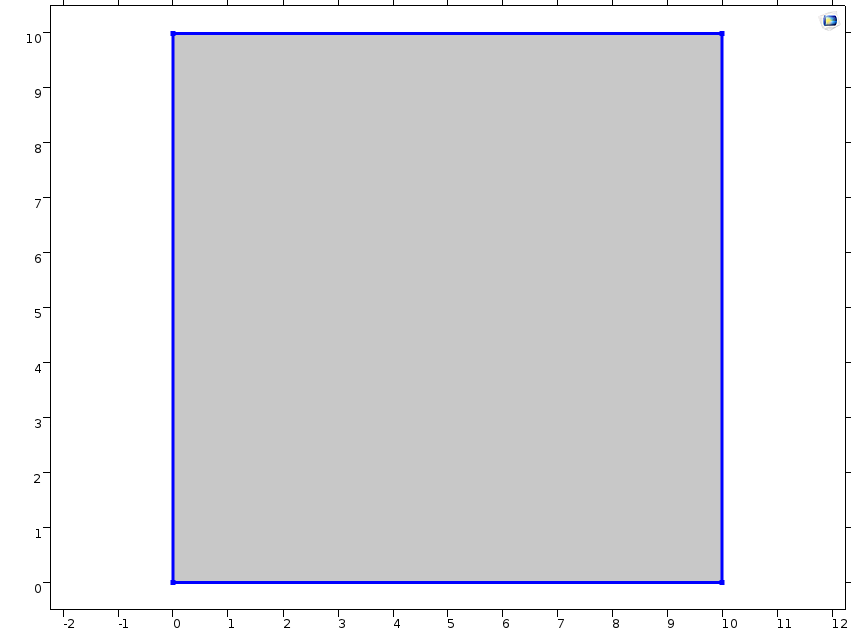
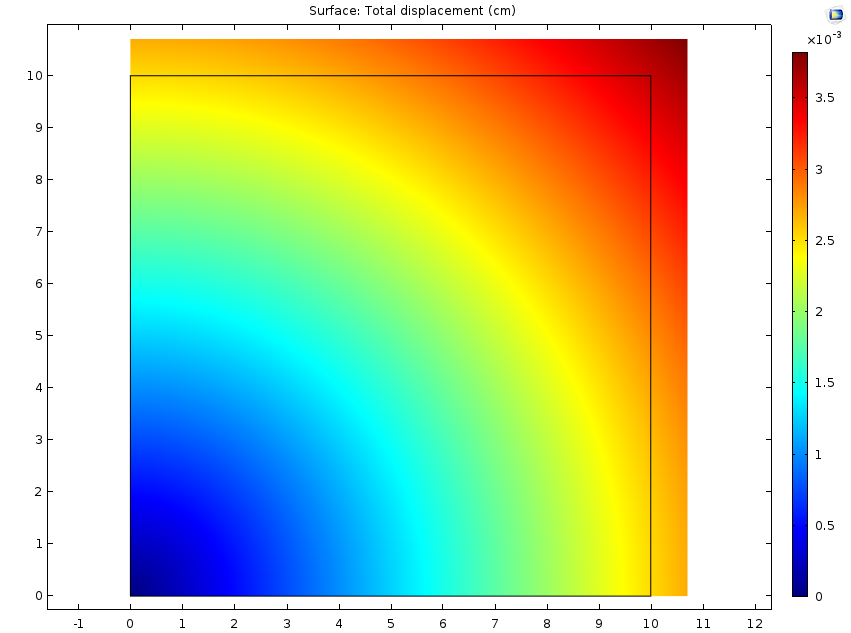
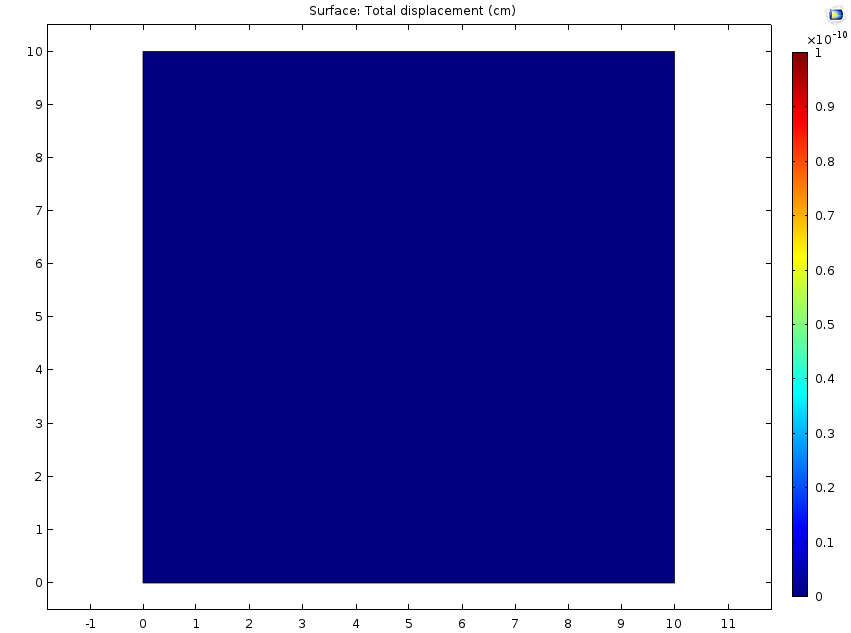
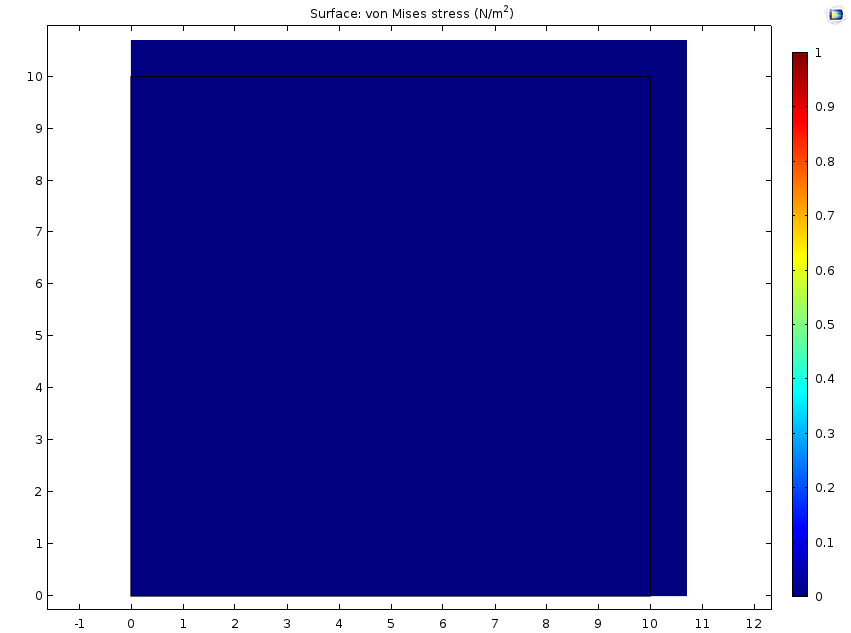
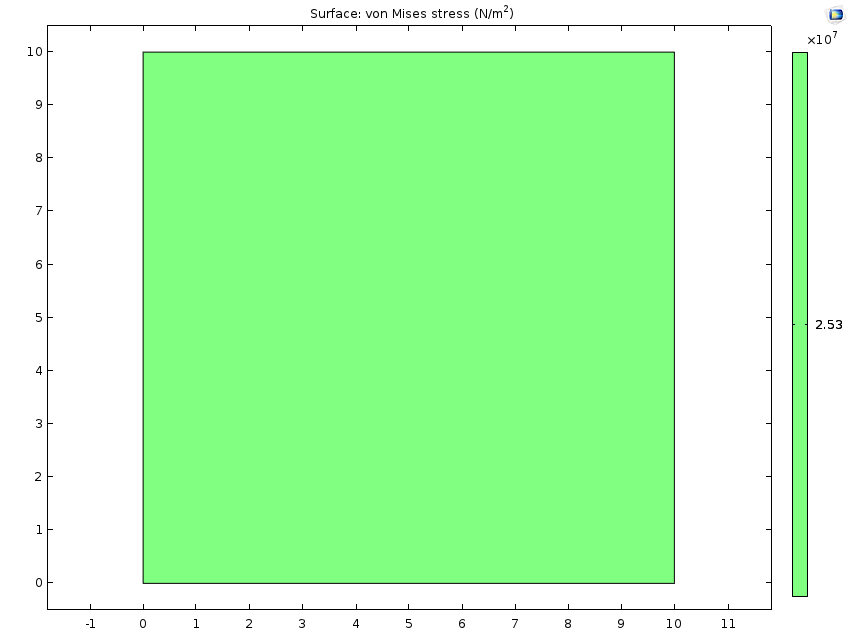
一个自由的固体(左栏)和一个完全约束的固体(右栏)在恒定的水分浓度下受到吸湿膨胀的例子。第一行显示了施加在每个固体上的辊支承。仿真结果绘制了第二行的位移场和第三行的 Von Mises 应力。自由的固体只受到两个辊支承约束,使实体能够膨胀并完全释放应力。相反,被周围的辊支承条件约束的固体没有膨胀,但应力增加了。
定义水分浓度和参考浓度
根据所选择的水分浓度类型(2),将浓度定义为质量浓度( C_\textrm{mo} 和 C_\textrm{mo,ref})或摩尔浓度( c_\textrm{mo} 和 c_\textrm{mo,ref})。由于 C_\textrm{diff} 是质量浓度差,当使用摩尔浓度输入时,还必须指定摩尔质量 M_\textrm{m}(4)。 M_\textrm{m} 的默认值是水的摩尔质量 0.018 \; \textrm{kg}/\textrm{m}^3。
\begin{array} {ll} \epsilon_\textrm{hs}=\beta_\textrm{h} M_\textrm{m} \left(c_\textrm{mo}-c_\textrm{mo,ref} \right) \end{array} 为摩尔浓度
\begin{array} {ll} \epsilon_\textrm{hs}=\beta_\textrm{h}\left(C_\textrm{mo}-C_\textrm{mo,ref} \right) \end{array} 为质量浓度
浓度(1)可以是用户定义的,也可以由另一个物理场接口计算。与 COMSOL Multiphysics 的任何输入一样,用户定义的值可以是其他变量的函数,如空间坐标 X、Y 和 Z。
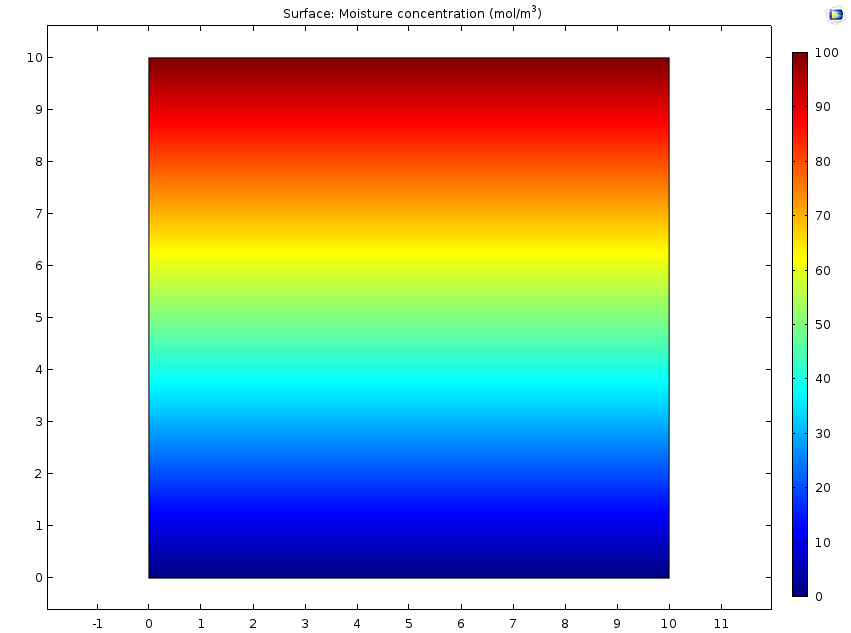
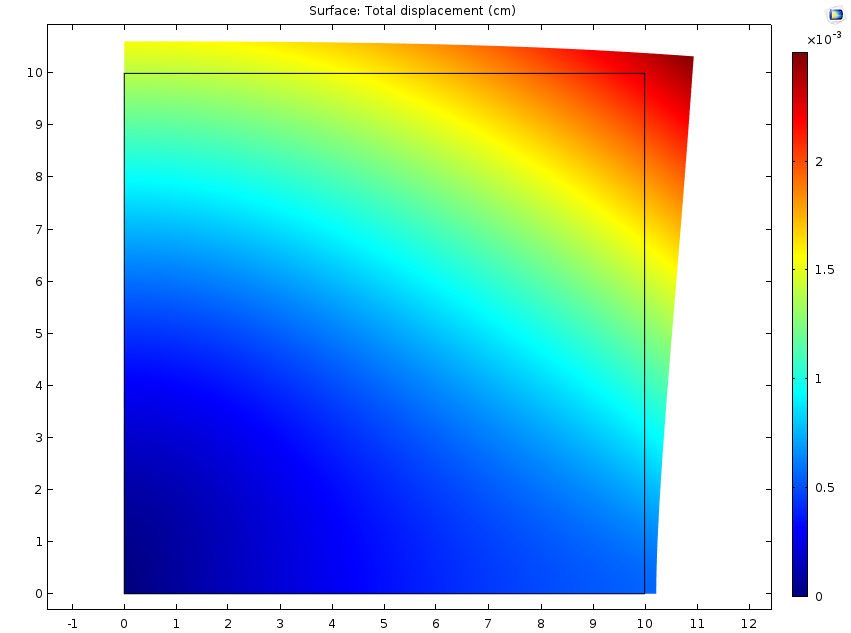
左图:用户定义的、与空间有关的水分浓度。右图:由吸湿膨胀引起的位移。顶面浓度最高,显示出最大的位移。
应变参考浓度(3)是指没有发生吸湿膨胀效应时得水分浓度。它通常可以被解释为初始状态,或出厂时的水分浓度。高于参考浓度的水分浓度代表湿润,并导致固体膨胀。低于参考浓度的水分浓度代表干燥,导致固体收缩。
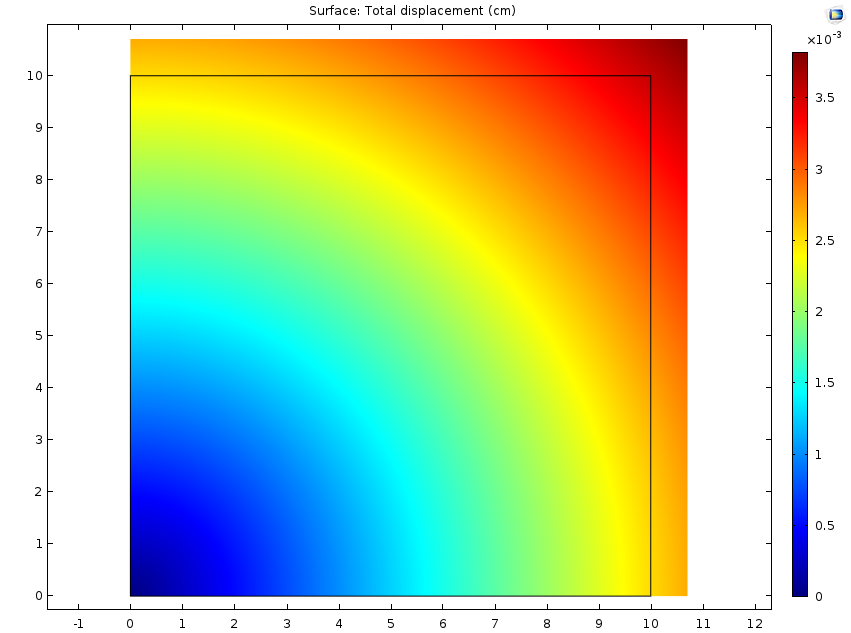
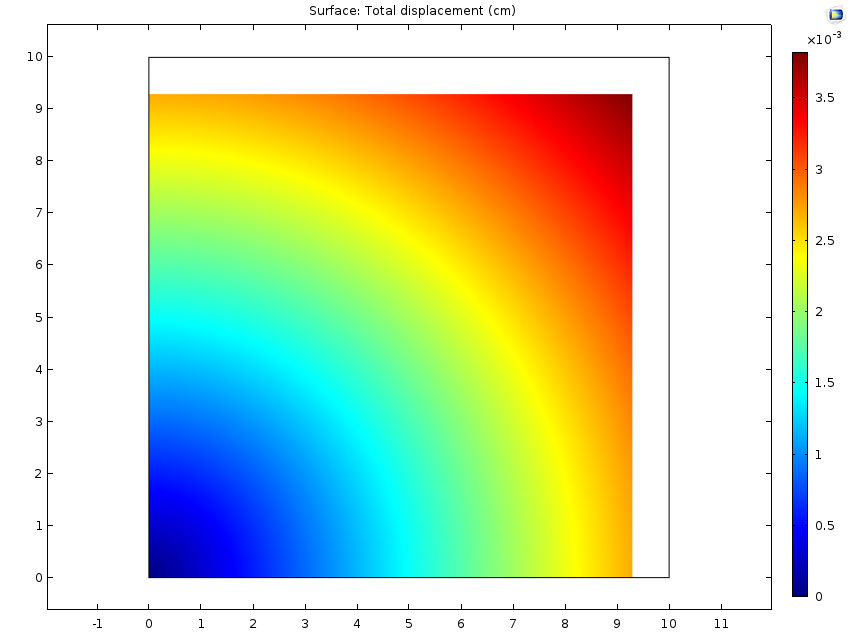
左图:零应变参考浓度下的位移。右图:非零应变参考浓度下的位移。两种情况下的施加的浓度相同,但低于应变参考浓度,意味着固体会收缩。
多物理场耦合
通常情况下,固体中的水分浓度是未知的,必须通过前面的仿真计算出来。您可以用稀物质传递 接口或多孔介质中的稀物质传递 接口来计算浓度。在 COMSOL Multiphysics 5.1 版本中的吸湿膨胀引起的 MEMS 压力传感器漂移案例模型中,就采用了这种方法。
将计算出的浓度输入固体力学 接口的一种方法是,在吸湿膨胀功能的组合框中指定所需的浓度变量。但是,我们还有一种更简单的方法。
在 5.1 版本中,您可以使用多物理场耦合,当模型树中至少有一个固体力学接口和一个传递物理场接口时,该耦合就可用。有了这个耦合功能,您只需要指定浓度来自哪个传递接口,以及要应用吸湿膨胀的固体力学接口就可以了。您还需要为所有选定的域设置参考浓度、摩尔质量和吸湿膨胀系数。当使用多物理场耦合时,您不需要在材料模型中添加任何吸湿膨胀的子节点。
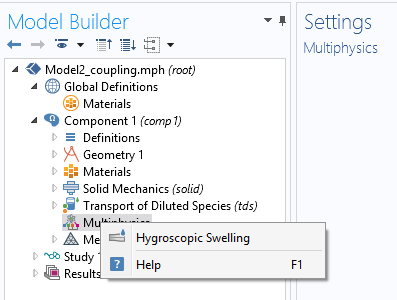
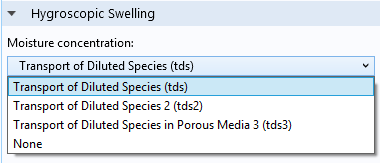
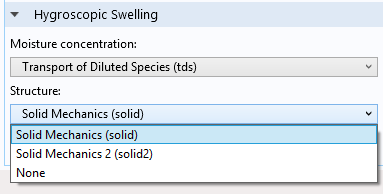
在多物理场耦合节点中选择参与的物理学接口,用于吸湿膨胀。
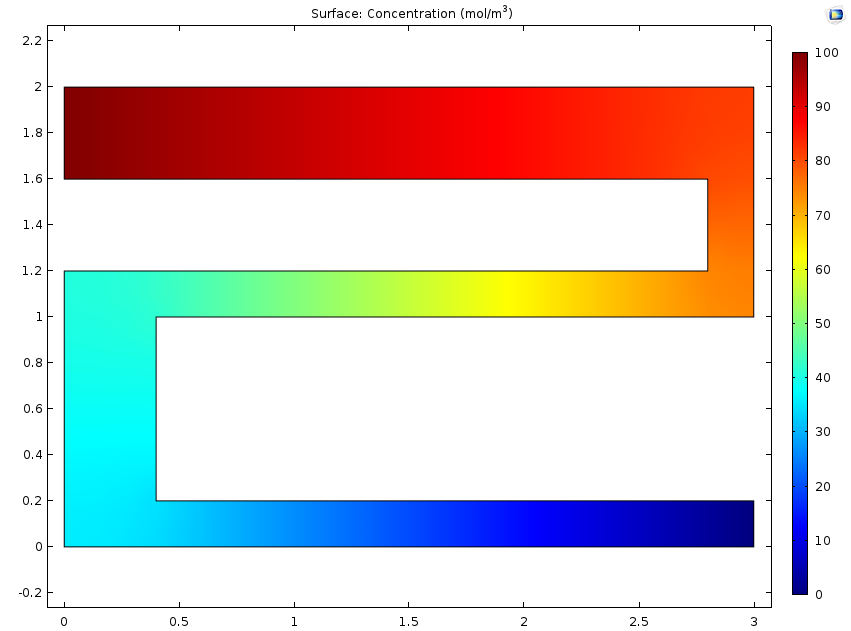
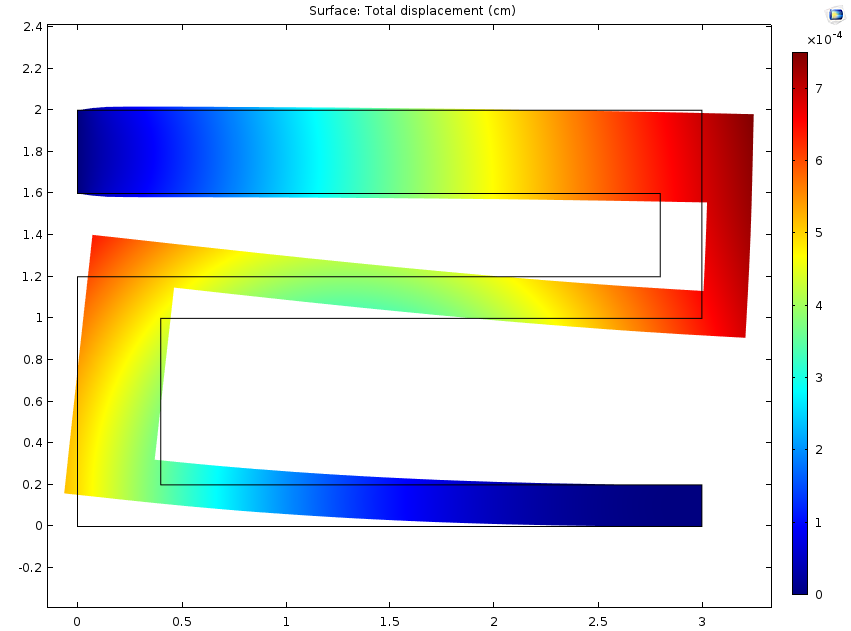
左图:在 稀物质传递接口计算的水分浓度。 右图:由吸湿膨胀引起的位移。
弯曲:梁、壳和板
在梁、壳 和板 接口中,水分浓度输入被划分为中心线或中间表面的平均浓度,以及横向方向(s)的浓度梯度。后者会导致结构的弯曲。
梁 接口的吸湿膨胀的输入包含了局部 y- 方向和 z- 方向的浓度梯度。在壳 和板 接口中,输入包含顶面和底面之间的浓度差。
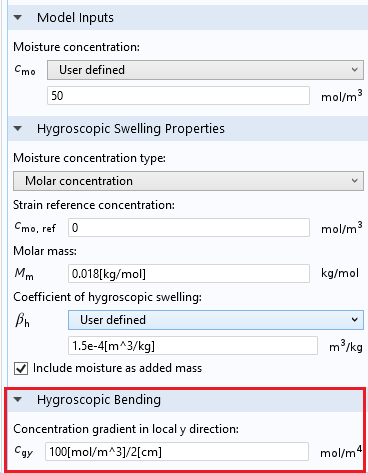
二维 梁接口中的吸湿弯曲。
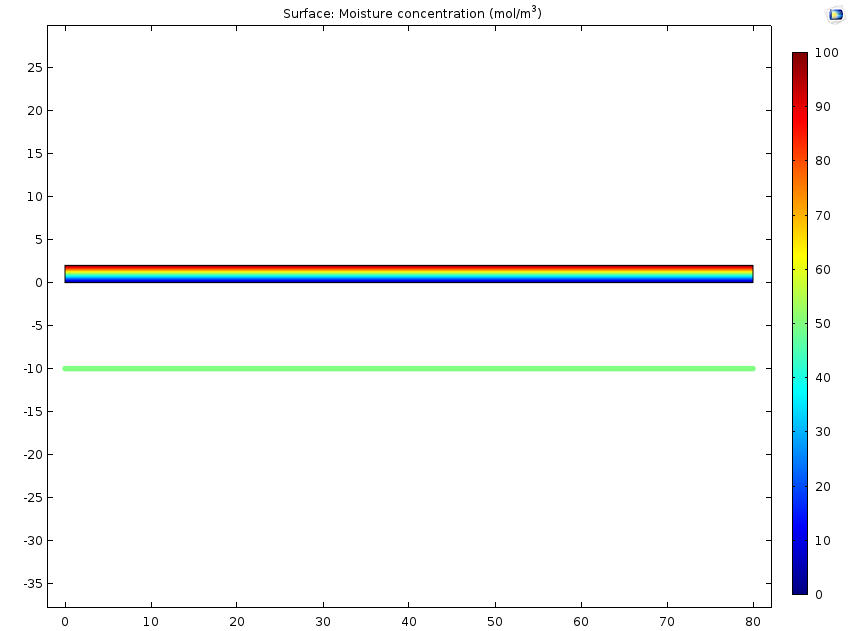
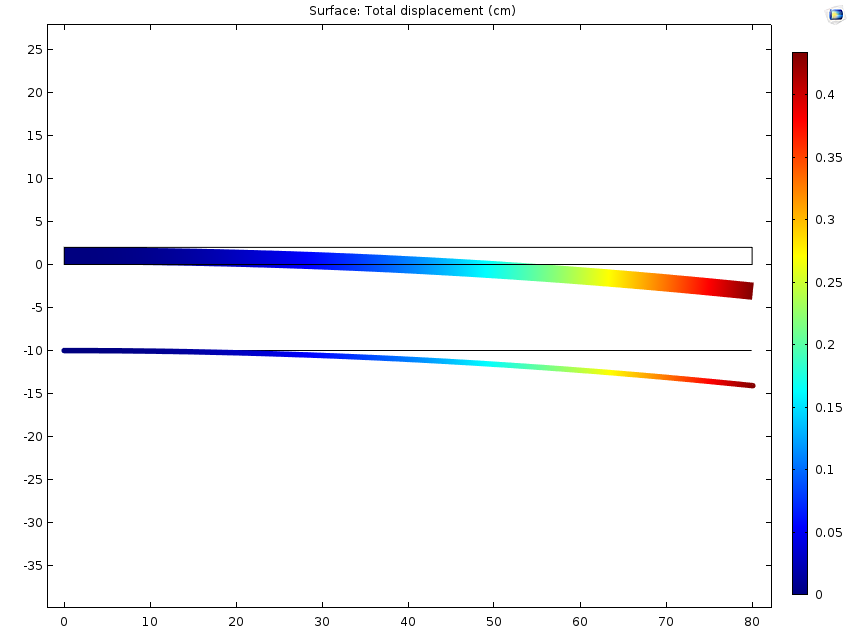
左图:水分浓度。右图:吸湿膨胀导致的位移。在实体中,弯曲是由非均匀膨胀引起的,它在顶面比底面高。在梁中,由同样的效应引起的弯曲使用水分梯度 c_{\textrm{g}y} 表征 。在这两幅图中,实体模型被放在梁模型的上方。
附加质量
当“将水分作为附加质量包括在内”复选框被标记时(6),被实体吸收或释放的水的重量将对与质量有关的现象产生影响,如重力或旋转坐标载荷。它也会对时域或频域研究中的惯性项产生影响。
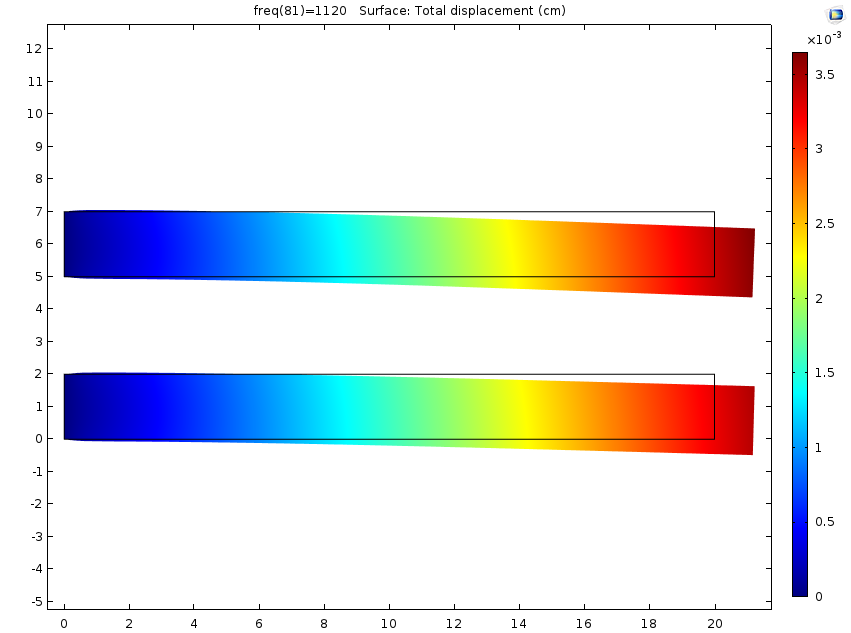
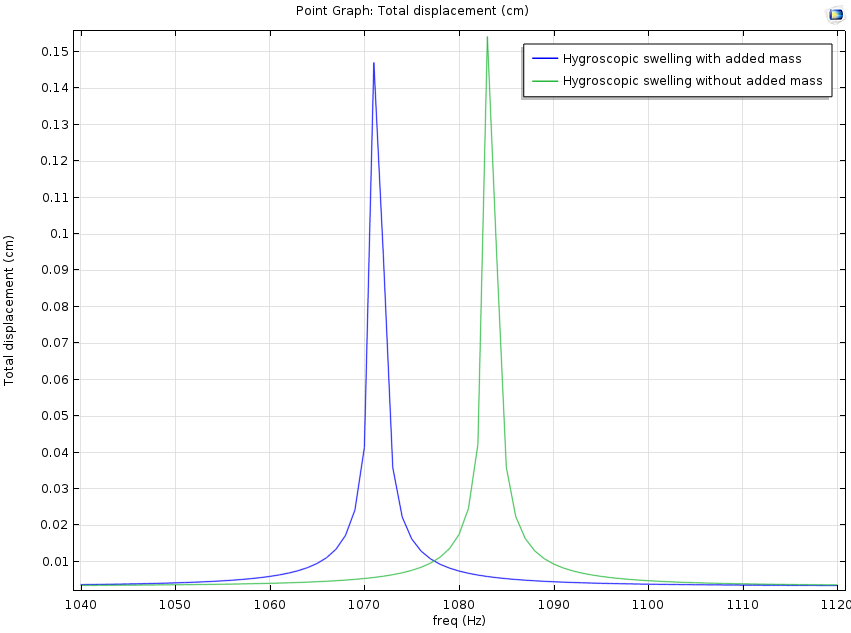
左图:当其中一根钢筋受到吸湿膨胀的影响时,用频率扫描分析两根钢筋的位移。右图:两根钢筋的频率响应。在吸湿膨胀过程中吸收的水增加了质量并降低了共振频率。
总质量,包括水质量吸收,可以在定义下的质量属性节点中计算。质量变量可用于后处理,与测量的固体质量进行比较,这是在现实生活中计算水分浓度的一种方便方法。
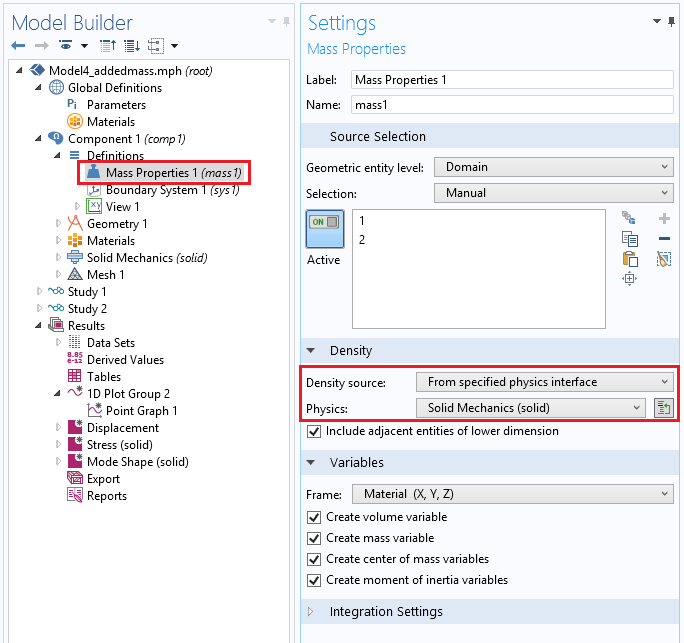
质量属性节点的屏幕截图。
总结
在许多设备设计中,考虑吸湿膨胀是很重要的。通过分析不同材料对该效应的反应,可以优化您的设计,以防止部件失效,并确保设备按预期运行。在这篇博客中,我们展示了COMSOL Multiphysics中的吸湿膨胀功能为什么是分析这种效应的有用的方法。利用吸湿膨胀功能,您可以准确且高效地量化吸湿膨胀的影响。
延伸阅读
- 下载教程模型:吸湿膨胀引起的MEMS压力传感器漂移
- 请在 COMSOL Multiphysics 5.1 版本发布亮点页面上阅读更多关于吸湿膨胀的多物理场耦合功能的信息。



评论 (0)