
你可能偶尔会遇到这样一个问题:能不能计算单根直导线的电感?这个看似简单的问题实际上并没有真正的答案,并引出了一个在求解麦克斯韦方程时值得讨论的非常有趣的关键点。每一个计算电磁学领域的人都应该了解这个关键概念,因为它将帮助你正确建立和解释涉及磁场的模型。
什么是单根直导线的电感?
在了解这一概念之前,让我们来回顾一个问题:什么是单根直导线的电感?要解决这个问题,首先要考虑基于能量的电感的定义:
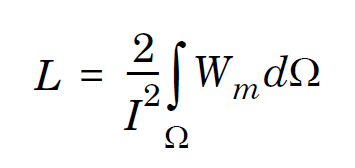
电感 L,由流过系统的电流 I 和磁能密度 Wm 定义,磁能密度与 B2 成正比。磁场 B 在导线的内部和外部均存在。在导线内部,磁场从中心线向外线性增加,在导线外部,磁场则以 1/r 的速度下降,其中 r 是半径。因此,为了计算磁场和磁能分布,我们基于麦克斯韦方程建立了一个模型,本例中为安培定律。在导线的一端施加一个电流源,另一端接地。在模型的外部边界上,磁通密度的法向分量被限制为零。
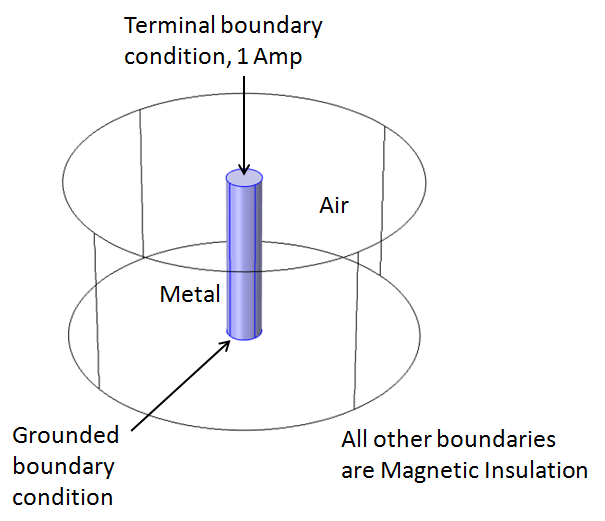
我们可以在 COMSOL Multiphysics 中使用 AC/DC 模块 的磁场和电场 物理场接口建立这个模型,求解导线中的电场和电流,以及导线和周围空气中的磁场。应用终端 边界条件激励结构,并使用上述方程自动计算电感。导线另一端的接地 边界条件提供了一个电流汇,而磁绝缘 边界条件则将磁通密度的法向分量设为零。
现在,磁场在导线周围无限延伸,但磁能密度以 1/r2 而下降,因此我们可以认为只需研究建模域半径的增加就足够了,并且电感量会收敛。但是,如果我们尝试这样做,电感与半径的函数关系将如下所示:
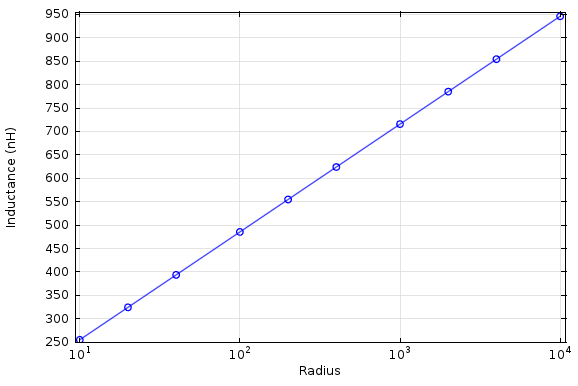
可以发现,随着半径的增加,电感也在增加。无论我们将建模域做得多大,这种直导线模型的电感都不会收敛!
不仅仅求解电感
如果我们连这种简单的情况都无法正确计算,那情况就太糟糕了,对吗?实际上,在这个模型中,我们并不只是求解导线的电感。你始终需要求解系统的电感,并且必须包括电流返回路径。麦克斯韦方程是在以下假设下制定的:电流(电子)既不能被产生也不能被破坏。事实上,磁绝缘 边界条件提供了电流返回路径。我们可以通过绘制体积中的电流以及表面电流来理解这一点:
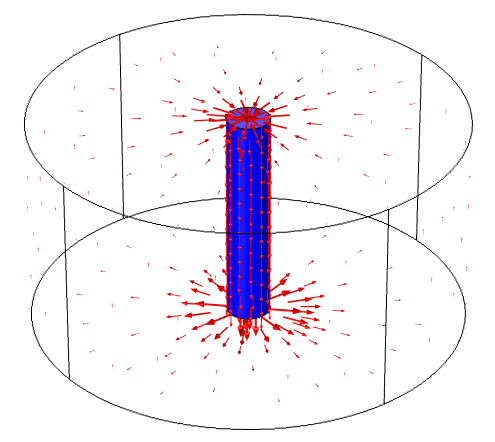
上图中的红色箭头表示电流沿着导线流动,同时也作为表面电流沿着磁绝缘 边界条件流动。我们可以认为磁绝缘 边界条件代表了一种具有无限电导率的材料,电流可以沿着这种材料畅通无阻地流动。上图中的电流路径是螺线形 的,即电流在封闭路径中流动。不仅有一条从终端到接地边界条件的导电路径通过导线,而且还有一条从接地边界条件沿边界返回终端的导电路径。
螺线管路径
电流的螺线管路径 概念是这里的关键点。无论什么时候,建立任何类型的磁场模型都必须确保电流能够在闭合回路中流动。你别无选择:这是麦克斯韦方程组的要求。你还必须意识到,电流回流路径会影响结果。在上述模型中,我们不仅要计算电流沿导线流动所产生的电感,还要考虑电流沿磁绝缘边界条件回流的影响。
在设置任何类型的磁场模型时,都必须建立一个完整的螺线管电流路径模型,而根据这样的模型计算出的电感是整个电流回路的电感。
这就是为什么无法计算单根直导线电感的原因!
当然,只要你分析的系统是螺线管系统,电流在环路中流动,就可以正确计算电感。
扩展阅读
参阅以下案例模型,查看计算圆环导线之间的互感并与解析解进行比较的示例:






评论 (0)