
COMSOL Multiphysics® 软件的核心优势之一是可以修改计算模型中的几乎所有表达式。我们必须谨慎使用这项功能,但是可以借助它实现其他很强大的功能。在这篇博客中,我们将以一个带有平移的二维(2D)热模型为例,先将某些材料属性设置为零,然后发现此问题变为类似于求解一维(1D)瞬态模型;最后思考这项功能是如何简便、快速地实现一些类型的优化问题。
将 2 个空间维度变为 1 个空间维度和 1 个时间维度
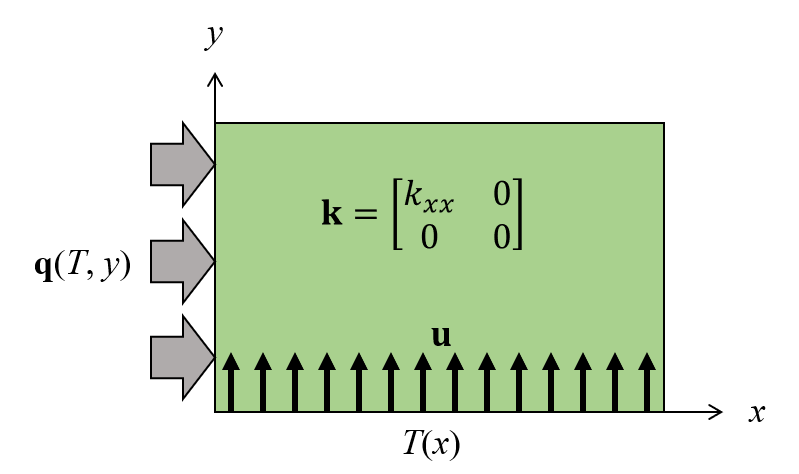
类似于 1D 瞬态模型的 2D 稳态热模型示意图。
考虑一个非常简单的矩形 2D 传热模型。 在没有体积热但有对流项的情况下,我们将求解温度的稳态(时间不变)传热控制方程,其表达式如下:
这里,\rho 是材料密度;C_p 是比热;\mathbf{k} 是热导率,用下面的对角矩阵形式表示:
0 & k_{yy}\end{bmatrix}
通过扩展所有项,可以更详细地写出控制方程:
{\partial x}+ u_y \frac{\partial T}{\partial y}\right) + \frac{\partial}{\partial x}\left(k_{xx} \frac{\partial T}{\partial x}\right)+ \frac{\partial}{\partial y} \left(k_{yy} \frac{\partial T}{\partial y}\right)= 0
现在,我们来做一件有意思的事情。假定速度矢量完全沿着 +y 方向上,因此 u_x = 0。将对角导热系数张量的 y 分量设置为零,k_{yy} = 0,以上等式简化为:
将导热系数张量的一项设置为零可能不常见,但这带来了一个好处:当我们写出 1D 瞬态传热控制方程时,没有体积加热或对流项,这一点就显而易见了:
请注意,以上两个方程中的第一项看起来几乎相同,如果我们正确选择速度项,那么上述两个方程将相同。现在,我们看到了一些非常有趣的现象:我们的 2D 稳态模型似乎与 1D 瞬态模型相同。
实际上,这些方程是相同的,但是当我们通过数值求解时,需要注意一些事情。首先,在 2D 域的底部边界应用固定温度条件类似于瞬态 1D 情况的初始条件。其次,对于这样的 2D 模型,具有映射的网格(与 y 轴对齐)是有意义的,并且可以将y方向上的单元数量视为固定的时间步。这与时域模型大不相同,后者默认情况下使用自适应时间步进。而 2D 模型还将(默认情况下)包含数值稳定项,这将使二者的计算结果略有不同,除非其中一个模型达到了较高的网格划分和容差细化水平。
那么,下一个问题是:我们该怎么使用这项功能?为了了解它的功能,让我们来看一个经典的 1D 传热模型,其中一块材料被加热,如下图所示。尽管该模型看起来很简单,但是工程上关注的许多问题都可以简化到这种经典情况。当从左侧表面加热材料时,整个材料逐渐变热但不均匀。同时,左侧还存在辐射冷却和一些自由对流,近似为恒定的传热系数。
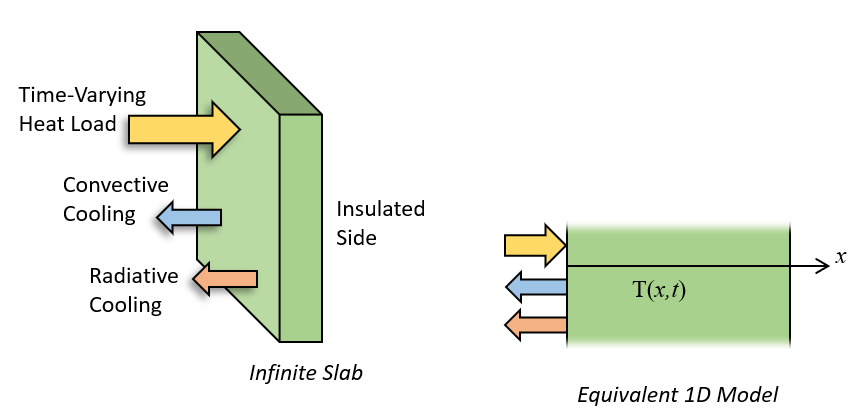
可以将材料板的 2D 瞬态加热模型降低为 1D 模型。
在 COMSOL Multiphysics 中,可以通过设置 2D 矩形域并使用固体和流体传热 物理场接口来解决这个问题。在这个接口中,我们可以将平移运动 子特征应用于固体 特征,对底部边界应用 温度 边界条件,左侧应用 热通量 和表面对环境辐射 特征来模拟对流冷却和辐射冷却,以及添加热通量 条件施加热负荷。在时间轴上具有均匀热负荷的一个模拟结果如下所示。
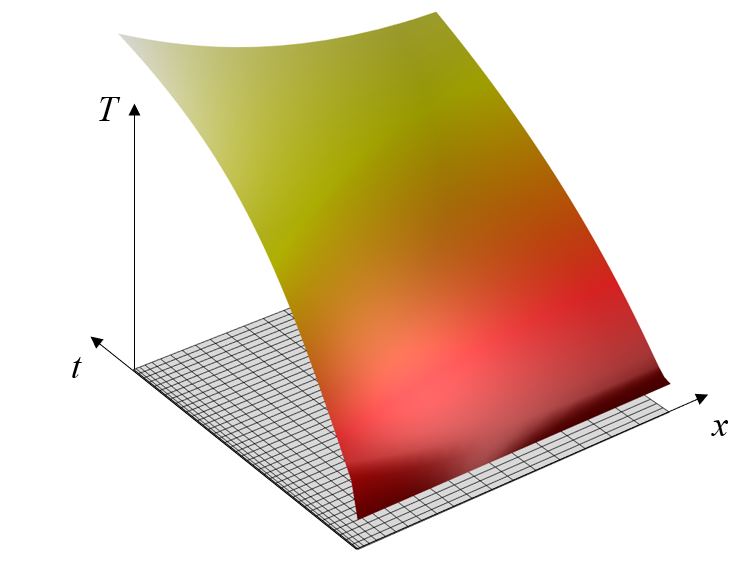
代表 1D 平板瞬态加热的 2D 稳态模型的模拟结果和网格。
现在,假设我们要优化此加热过程。让我们尝试跟随时间来改变施加的热负荷,以使整个平板的温度在模拟结束时尽可能地接近目标温度,并设置约束使峰值温度永远不会超过设定值。通过 1D 平板的 2D 模型,我们发现这个优化问题非常容易设置。下面,让我们看看如何实现吧!
定义优化问题
COMSOL 软件定义 节点下的拓扑优化 分支中的密度模型特征用于定义变量控制的时间热通量。这个特征在边界上定义了一个场,该场被限制在 0 到 1 之间,表示没有加热和最大加热。该场的离散化是线性的,这意味着在每个单元上热负荷随时间可以线性变化,并且热负荷可以在 ÿ 方向的网格大小确定的时间跨度上变化。这并不理想——这意味着热负荷的变化与我们的时间步一样快。相反,我们希望热负荷随时间的变化慢于离散化。因此,我们需要采取下一步骤,那就是引入亥姆霍兹过滤器(Helmholtz filter)。这在拓扑优化领域中是很常见的作法,并且可以在设置节点的过滤 部分实现。过滤半径 需要稍大于网格尺寸,并表示一个平滑的时间。该过滤后的控制变量场的名称为 dtopo1.theta,并乘以入射热通量。
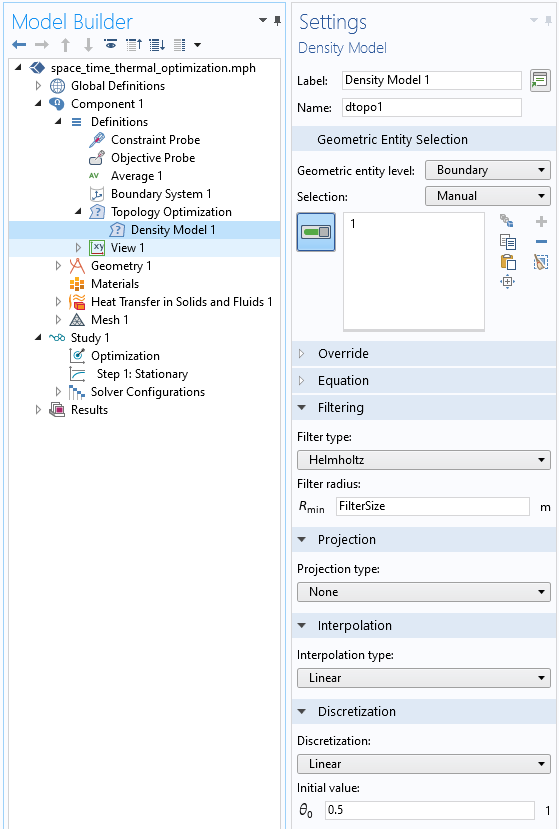
拓扑优化密度模型特征的屏幕快照,它沿板的受热面定义,并在代表时间的整个轴上定义。
下面屏幕快照中显示了我们的目标表达式,它是一个在顶部边界(代表最终时间)的积分探针。积分 的表达式基于计算出的解 T 和想要达到的温度 T_target。通过定义一个目标,即该边界上计算出的温度与目标温度之间平方差的积分,我们得到一个微分函数,当最终温度尽可能接近目标时,该函数具有最小值。我们定义的目标名称是 comp1.obj,我们将从优化 研究步骤中引用该目标。
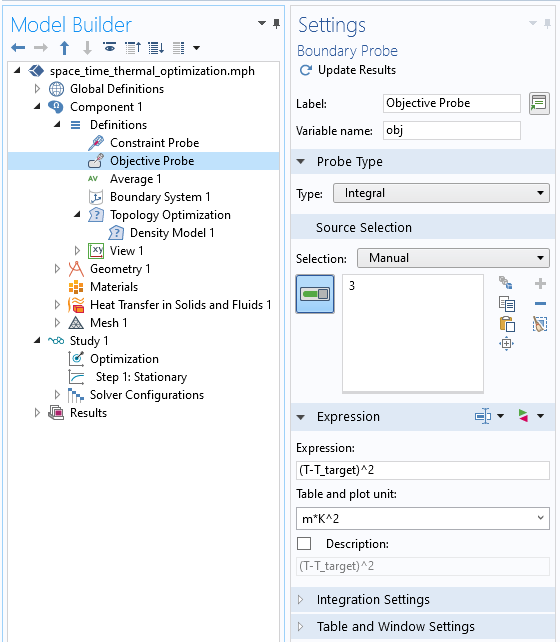
在顶部边界定义的目标探针特征的屏幕快照,定义了我们要最小化的目标表达式。
我们在优化 接口中定义了一个约束,即:
comp1.constr < 1
如上面的屏幕快照所示,该表达式 comp1.constr 是通过一个全局变量探针 定义的。该表达式首先取以下平均值:
在加热边界上,取 p_{exp} 一根。这是P 范数。如 p_{exp} 接近无穷大时,此约束将强制温度不沿着加热边界升高到最高温度以上。现在,由于数值原因,p_{exp} 不能是无穷大即不能完全满足此约束,但是如果 p_{exp} 足够大,则约束可以近似满足。如果 p_{exp} 设置过大,则我们将引入一个极度非线性的约束函数,它会减慢收敛速度,并且还会出现一些可能的数值溢出问题,因此可以将此值视为模型中的调整参数。
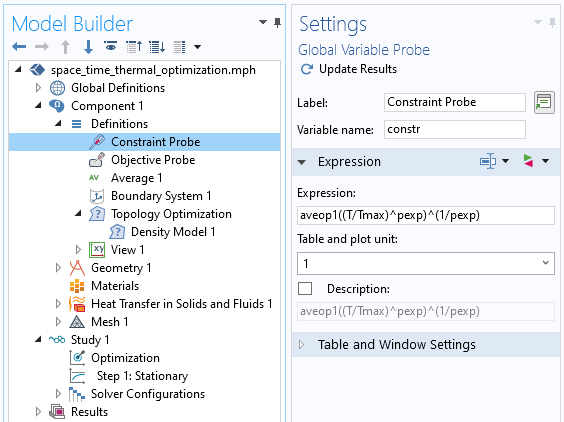
屏幕截图显示了定义约束表达式的探针。
作为优化模块的一部分,我们使用研究分支中的优化研究步骤引入变量、约束和控制参数。目标和约束可以是全局变量,例如上面提到的探针。下面我们来看看这种情况如何设置。
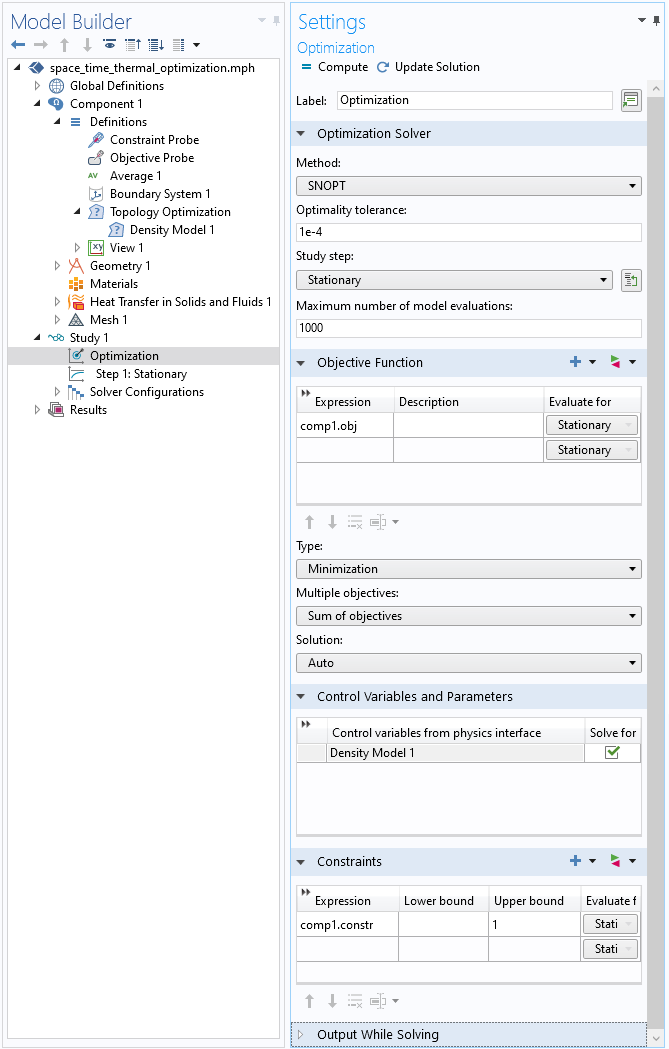
“研究”分支中的“优化”研究步骤的屏幕快照,定义了优化求解器类型、目标、设计变量和约束。
上面的屏幕截图显示了研究 分支中的优化 研究步骤。在此特征下,我们定义了优化求解器、目标函数、设计变量和约束。在设置的顶部,我们看到使用了 SNOPT 求解器。该求解器期望目标函数和约束相对于设计变量是可区分的。在优化容差 和模型最大计算次数 将 支配 求解器将采取多少次迭代尝试找到最优值。接下来的三个部分定义了目标函数、控制变量和参数 以及约束。
定义了目标函数、设计变量和约束后,现在只需求解模型即可。
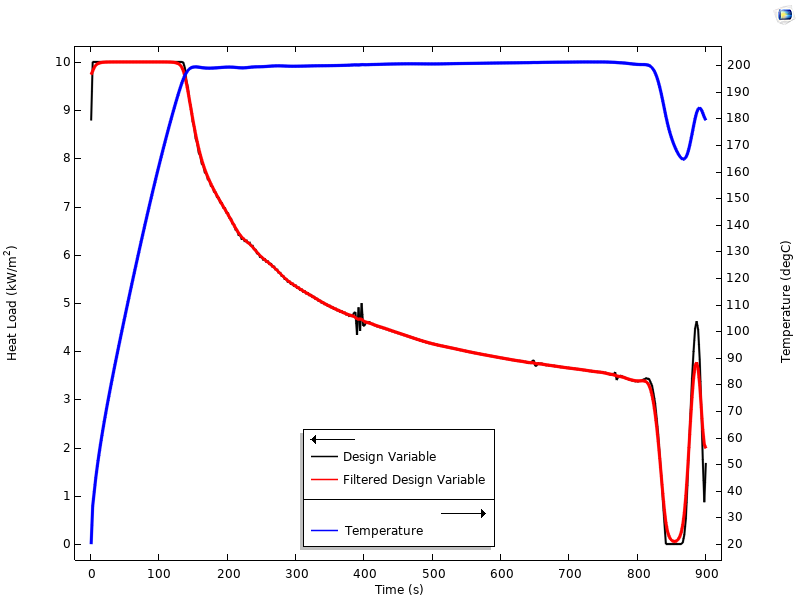
沿时间轴绘制的设计变量,过滤设计变量和温度图。
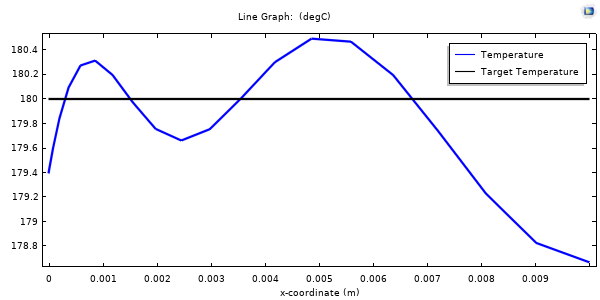
最终时间的温度(蓝色)与目标温度(黑色)比较,表明温度场在 1D 域中非常接近目标温度。
这个包括导热系数的非线性材料模型,需要约一分钟的时间优化得到上图所示的解决方案。该解决方案绘制了板加热边随时间变化的温度,还有过滤后的变量和未过滤的设计变量,以及板横截面的最终温度。我们观察到的特别有趣的现象是:优化求解器找到的解决方案为,在刚开始的时候为加热峰值,然后热载荷逐渐减小,以不超过峰值温度的限制,当整个板的温度场趋于最佳,热载荷逐渐趋于零,最后在短时间内增加了加热量,以抵消环境冷却。
这时,我们可能会问自己这种方法的优点是什么?实际上,我们也可以单纯地在时域中解决整个优化问题。那么我们使用这种方法获得了什么呢?答案是:速度和简便性。
通过重新设计为时间空间函数,我们解决了稳态优化问题,该问题比求解瞬态优化问题要快。我们还可以使用内置的拓扑优化功能,包括亥姆霍兹过滤器,可以很容易地设置随时间任意的、受约束的、平滑的强制函数。那么,除了一些概念上的复杂性之外,这种方法的缺点是会占用更多的内存。通过同时求解空间和时间,系统矩阵与时间轴的网格成比例地变大,并且该网格必须在仿真之前固定。但是,对于这种 2D 模型,即使具有非常精细的网格,内存要求也并不太高。
具有两个空间维度的模型的内存需求确实会变大,但并不是很大。下面的链接提供了一个类似的二维模型优化,其第三维度代表时间维度的案例,这个案例包括电流和传热耦合计算焦耳热,时间优化,并使用了和刚才介绍的相同的技巧,祝您建模愉快!
动手尝试
尝试使用时空模型优化随时间变化的热负荷。单击下面的按钮访问模型文件。(注意:您需要使用有效的软件许可证登录到 COMSOL Access 帐户才能下载 MPH 文件。)



评论 (0)