如何利用多物理场射线追踪分析激光腔的稳定性

激光是现代科学中最有用的发明之一，但它使用起来并不容易。仅当腔镜完全对准时，激光器才能工作。即使激光发射了一段时间，它也可能突然停止。在今天的博客文章中，我们将讨论如何使用 COMSOL Multiphysics^® 软件中的射线追踪功能来预测激光稳定性。

激光仿真导论

Albert Einstein（爱因斯坦）于 1916 年发现了受激发射。但这种激光大约是在 1957 年，由三位美国科学家 C.H. Townes，A.L. Schawlow 或 G. Gould 中的一个发明的。（关于谁首先发现了激光理论，有一场专利之争，而关于是谁提出这个想法也仍然有争议。）1960 年，Theodore Maiman 制造了第一台激光器。

激光在许多应用中都非常有用，例如切割、穿孔、熔化、烧蚀、无线电通信，测量和光谱学等。1960 年代，A.G. Fox，T.Li 和 H. Kogelnik 通过基于光学近轴理论的计算场分布，提出了高斯光束和预测激光稳定性的方法，在激光研究方面取得了进一步的进展。即使在六十年后的今天，这些理论仍然是处理和设计激光器的基础。

在这些理论中，Kogelnik 的激光稳定性理论对激光工程特别有用。该理论包括两个部分：

1. 近轴光学理论可预测激光腔中产生的高斯光束
2. 几何光学理论可预测激光束何时在腔中保持稳定

由于热透镜效应，激光打开或泵浦后可能会停止工作。激光晶体被另一个光源或多个光源泵浦会引起粒子数反转。该过程中，由于泵浦光的剩余能量产生不期望的热量，这些剩余能量不用于诱发受激发射。不期望的热量导致不期望的折射率变化，并导致晶体表面膨胀。

Kogelnik 的理论涵盖了包括柱状透镜在内的所有激光腔，通过抛物线拟合晶体中的温度分布来近似热透镜效应。

一种掺钛蓝宝石飞秒激光器。来自 Ar 激光器的绿色激光用于泵浦 Ti：蓝宝石晶体，发出橙色的眩光，以进行粒子数反转。）激光晶体是一个圆棒，但是有一个倾斜的切口，称为布鲁斯特切口（Brewster cut）。泵浦光束以布鲁斯特角（Brewster angle）进入晶体表面，以避免不期望的菲涅耳反射（Fresnel reflections）。图片来自 Hankwang 自己的作品。通过Wikimedia Commons在CC BY-SA 3.0下获得许可。

分析激光稳定性的方法

Kogelnik 理论的稳定性思想非常简单：如果经过一定数量的往返行程后，在激光腔镜之间来回反弹的光线没有从腔中逸出，则激光束是稳定的。该理论通过使用基于近轴光学而不是真实射线追踪的 ABCD 矩阵理论，更加简洁和有条理。

在这个理论中，热透镜被建模为具有一定焦距的薄透镜。通过利用抛物线拟合的激光晶体中的温度分布来计算焦距。因此，ABCD 矩阵理论和抛物线拟合方法很容易执行，并能产生理想的结果。我们只需要知道光学元件的距离、所涉及透镜的焦距以及反射镜的曲率半径即可。

所有折叠镜均由具有等效焦距的透镜代替，并且使用近似焦距表示热透镜效应，而不是给定的泵浦功率（以瓦特为单位）。光学器件不能倾斜，光学布局可以直线地展平为一维。

这种方法太简单了，因此无法处理更复杂、更实用的激光腔。如果要以3D的形式查看结果或在稳定性分析中添加棱镜，该怎么办？如果要通过折叠镜折叠激光束或倾斜其中一个光学元件怎么办？给定泵浦功率，而不是近似的焦距，该怎么办？另外，为什么不进行任何限制或近似的光线跟踪和热分析？

在不考虑热透镜效应的情况下执行激光器稳定性分析几乎是无用的，因为每个激光器都会被泵浦。因此，我们需要进行与稳定性分析相对应的热分析，它不能与射线追踪分开分析。通过在 COMSOL Multiphysics 中耦合传热 和几何光学 接口，我们可以获得所需的所有工具。

在 COMSOL Multiphysics^® 中分析具有共焦腔的激光器

下面,我们来看一个简单的激光腔示例模型，并简要概述 ABCD 矩阵方法的工作原理以及它与 COMSOL Multiphysics 仿真结果的一致性。本节补充了 Kogelnik 自己的一篇研究论文的一部分（参考资料1）。在 ABCD 矩阵方法中，遵循 Hecht 表示法（参考文献2），光线可以由一个 2×1 阶列向量中的光线角度 θ 和光线位置 y 表征为

所有的光学过程，包括传播、折射、反射、聚焦和散焦，都由称为射线传输矩阵的 2×2 矩阵表示。

例如，通过距离 L 的传播由一个 2×2 矩阵表示

在空气中一个曲率半径为 R 的镜子上的反射可以表示为

示例激光腔中具有一对相同的反射镜，其曲率半径为 R= 0.1m，腔体长度 L=R/2=0.05m。该腔体如下图所示，称为“共焦腔”。

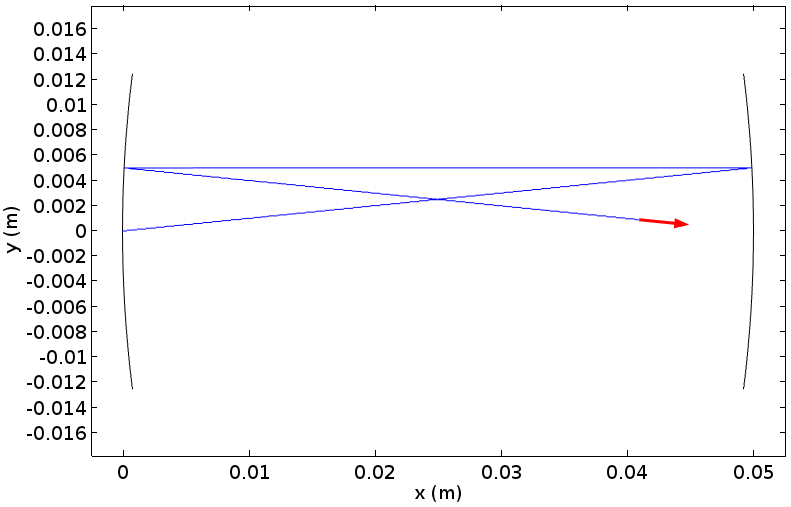
几次反弹后，在 COMSOL Multiphysics 中对共焦腔进行射线跟踪。

将 θ₀= 0.1rad 和 ÿ₀=0.01m 设置为初始射线角度和位置。（对于 ABCD 矩阵方法，x 的位置不重要，将初始光线设置为 x=0m，即在左镜的中心。）由 ABCD 矩阵方法可知，沿腔体长度传播的射线位置和下一个角可以由下式计算

这是右反射镜上的光线角度和位置（在反射之前）。反射后，下一个射线角度和位置仍在右反射镜上，但朝向左。它们可以由下式计算

然后，沿腔体长度的另一次传播使光线返回到原来的左镜，可由下式计算

最后，经左镜反射后的一次往返的结束，由下式计算

该值可以在上图中得到确认。

这种方法的优点在于，我们仅需进行矩阵运算来了解射线的行为。我们可以计算出一个矩阵 M，它表示射线的传播和反射序列为

其结果与先前的结果相同：

该传递矩阵 M 具有 M³＝I 的性质。即，经过三个往返之后，它变成单位矩阵。实际上，这可以通过 Sylvester’s theorem （西尔维斯特惯性定理）进行分析证明，而无需计算矩阵乘积：

其中，\cos \Theta = (A+D)/2。

将 ñ=3 代入上面的公式中的 M 矩阵中，得到 M³=I。我们可以通过下图中的射线追踪来确认这一点，其中光线路径是由往返次数着色的。

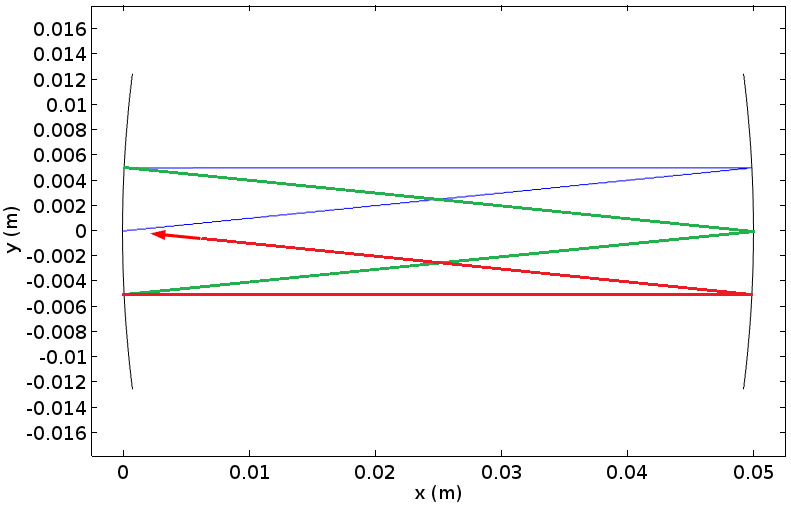
与前一个图相同的共焦腔的射线追踪结果表明，光线在往返 3 次后返回到了初始位置。

在这种情况下，可以说该腔体是稳定的，这意味着该腔体内部的射线不会从中逸出。上面的公式可以得出这样一个普遍的结果：当矩阵的迹为 -1 \le (A+D)/2 \le 1 时，由矩阵表示的序列是稳定的。

在本示例中，矩阵的迹被计算为 (A+D)/2 = -1/2。因此，它是稳定的。

如下图所示，还可以通过绘制单位波矢量的 y 分量来查看结果。该图显示，射线方向会定期改变，但不会增长，并且在 3 次往返之后会返回相同的值。大体上，±0.15rad 是射线进入腔体内的上下边界，下图证明了这种情况。

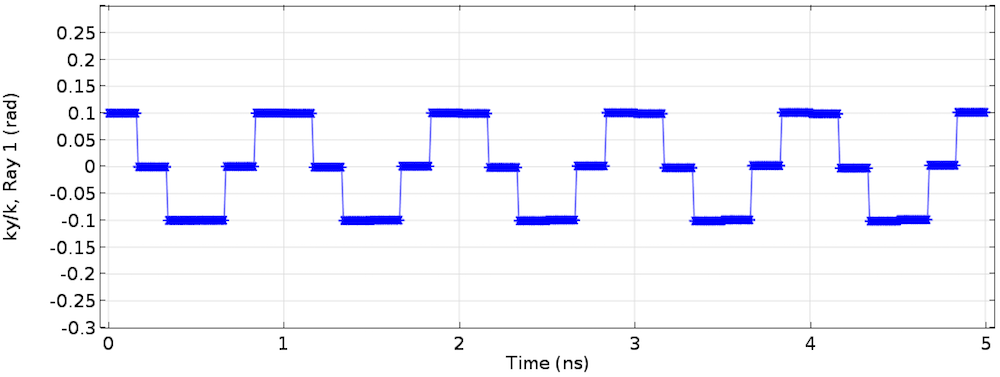
单位波矢量的 y 分量。射线的方向以有限的最小和最大值为边界，这意味着射线不会偏离到腔镜之外。

更改激光器的腔体长度

下面我们来讨论另一个例子。选择腔体长度为 L=R\left(1-\sqrt{1+\cos(9 \pi/10)/2}\right)=0.084357 m。该腔体距离共焦腔有点远。这种有意调整的空腔长度可确保 \sin(20\Theta)=0 和 \sin(19\Theta)=-\sin(\Theta) 。因此，在经过 20 次往返之后，传递矩阵变成了单位矩阵，并且获得了初始射线角度和位置。这时，传输矩阵为

该传输矩阵的 20 次乘积为 M²⁰=I。我们可以通过下图中的射线追踪来确认这一点。红色箭头确实指向原镜的中心并指向原方向。

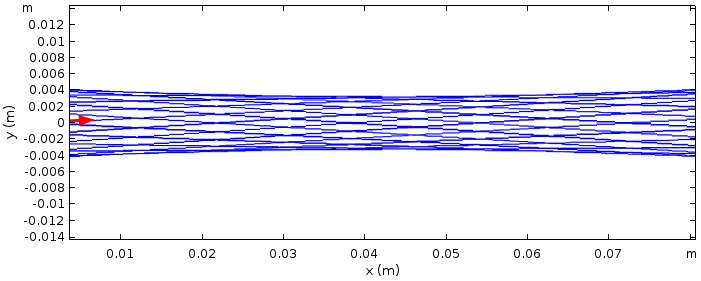
经 20 次往返之后，具有相同反射镜且腔体长度稍长的激光腔的射线追踪结果。

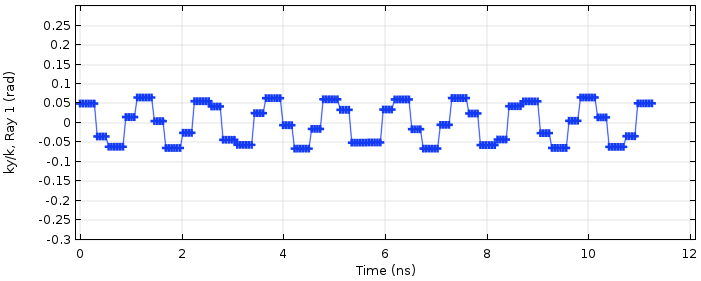
单位波矢量的 y 分量。

通常，曲率半径为 R₁ 的右反射镜，半径为 R₂ 的左反射镜和一个行程的腔长 L 的传输矩阵可写为

经过一些简单的运算，由矩阵的迹得出的稳定条件表示为

该稳定性公式可进一步扩展到在腔中包含透镜的情况。在腔体内引入透镜会使传递矩阵变得复杂，在这里不再写出，但是稳定性标准仍然很简单。添加焦距为 f 的镜头，将稳定条件修改为

其中，L₀=L₁+L₂–L₁ L₂/f，L₁ 和 L₂ 分别是从镜头到左、右镜的距离。在前一个腔中添加一个焦距为 f= 50mm 的聚焦透镜，其稳定性标准数为 0.10978，这可以预测该腔是稳定的。

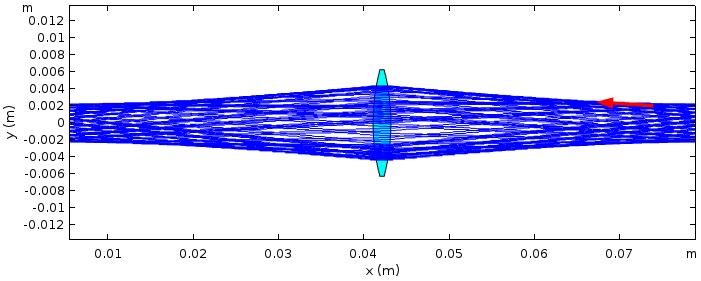
在之前的腔中添加了薄透镜的射线追踪结果。

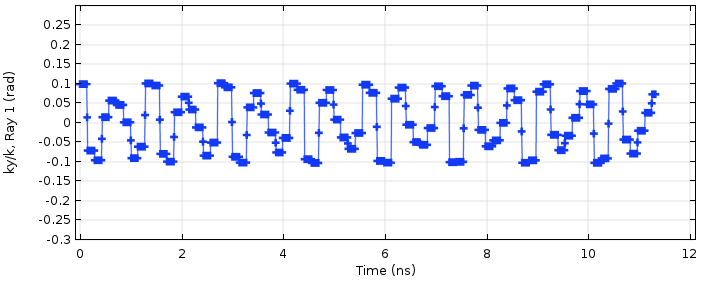
单位波矢量的 y 分量。

到目前为止，我们已经通过 ABCD 方法与 COMSOL Multiphysics 中的射线追踪功能研究了一些基本的激光腔稳定性分析。两种方法的稳定性结果吻合良好。

模拟焦距变化的激光器

现在，我们来看最后一个示例。在本示例中，对上一个示例中的焦距进行了参数化和更改，并在著名的稳定性图表中绘制了腔稳定性的变化。在 Kogelnik 的理论中，通过使用由 g₁= 1 –L₂/f–L₀/R₁ 和 g₂= 1 –L₁/f–L₀/R₂ 定义的一组新变量，将之前的稳定性条件公式改写为

在下面著名的稳定性图中，以 g₁ 和 g₂ 分别作为水平轴和垂直轴，将稳定区域绘制为阴影线区域。如果由原腔体参数 R₁，R₂ 和 L₀ 导出的 g₁ 和 g₂ 在阴影区域内，则根据Kogelnik的理论，激光腔是稳定的。对于前面的示例，我们为两个反射镜设置了相同的曲率半径。因此 R₁=R₂，因此 L₁=L₂=L₀/2 对称，这导致 g₁=g₂。这在稳定性图中表示为一个 45 度线。当腔体参数改变时，g₁ 和 g₂ 的值沿通过第一象限和第三象限的线改变。

接下来，我们来看看它是如何可视化的。将镜的曲率固定为 0.1m，腔长固定为0.084357 m，同时将透镜的焦距从 15mm 更改为 40mm（以 5mm 为增量）。下图显示了 Kogelnik 对带有透镜的特定激光腔的理论结果。对于f=25、30、35 和 40mm，激光是稳定的，g₁g₂ 分别为 0.67091，0.43100，0.29200 和 0.20545。

这些值被绘制在阴影区域，而焦距为 15 和 20mm 会使该激光器不稳定，因为它们的 g₁ g₂ 值超过 1.0，分别为 1.1299 和 2.1593。下图绘制了该激光腔的理论预测值。图的侧面为每个焦距的光线追踪结果，显示出与理论的完美匹配。在 COMSOL 计算中，一旦光线离开腔体，内置停止条件就会终止计算。实际计算时间 T 与预设计算时间 T₀（在这种情况下为 50ns）之比，T/T₀ 表示腔稳定性，如果 Ť₀ 选择适当。除 1.0 以外的任何稳定性指数值可能都无济于事，因为我们知道，当激光不稳定时，它会很快关闭。换句话说，激光稳定性的变化几乎是数字化的，即 1（打开）或 0（关闭）。

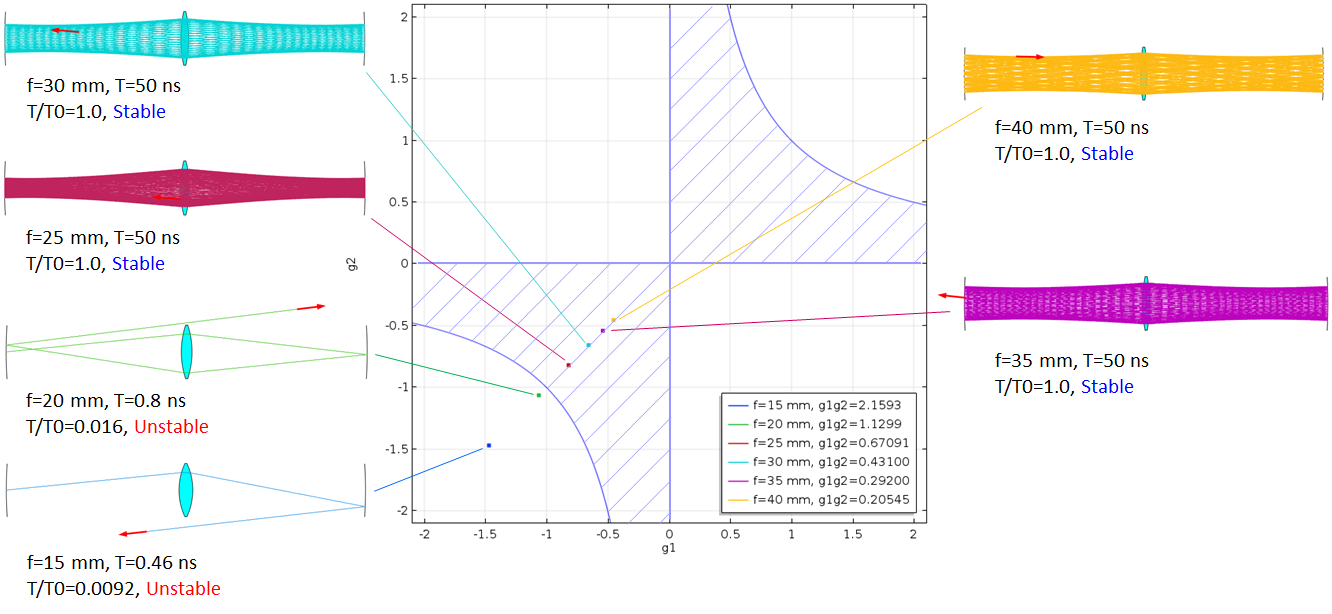
比较 Kogelnik 的稳定性理论和 COMSOL Multiphysics 带有薄透镜的共焦腔的射线追踪结果。

最后一个示例显示在考虑热透镜效应的情况下，射线追踪可以进行激光腔稳定性分析，因为该示例是 Kogelnik 的热透镜激光腔模型。按照 Kogelnik 的理论，由泵浦激光加热的激光晶体被具有一定焦距的薄透镜所代替。一旦知道了晶体内部的温度分布，就可以通过 n=n₀+（T–T₀）dn/dT 求出一阶近似值，其中 n，n₀ 是有泵浦和无泵浦的折射率分布，Ť，T₀ 是有和没有泵浦时的温度分布；dN/dT 是随温度变化的折射率变化。

如果晶体是棒状，则泵浦的激光晶体的折射率在中心附近的分布近似为抛物线形状，即 n（r=n₀（1-2 ²/a ²），其中 r 是极坐标系中的径向距离，其z轴沿着泵浦光轴。将计算出的折射率分布拟合到该抛物线以获得拟合参数 a。一旦该参数被计算出，即代表热透镜效应的焦距可以近似表示为 f〜a²/（4n₀ L），其中 L 是晶体长度（参考文献3）。热透镜效应还包括表面膨胀，这会引起折射角的变化，我们可以一种类似的方式对此进行分析。

结语

使用 COMSOL Multiphysics，我们无需进行拟合。我们只需使用传热 和固体力学 接口进行热和力学模拟，以了解新的折射率分布和表面膨胀，然后简单地使用射线光学接口进行射线追踪，以了解在热透镜效应下激光腔的稳定性。在即将发表的博客文章中，我们将进一步讨论 COMSOL Multiphysics 的射线追踪功能。在即将发表的这篇博客中，我们将会看到一个完整的对 Ti：蓝宝石激光腔的分析模型，该模型带有双泵浦布鲁斯特切口晶体和一对色散补偿棱镜。敬请关注！

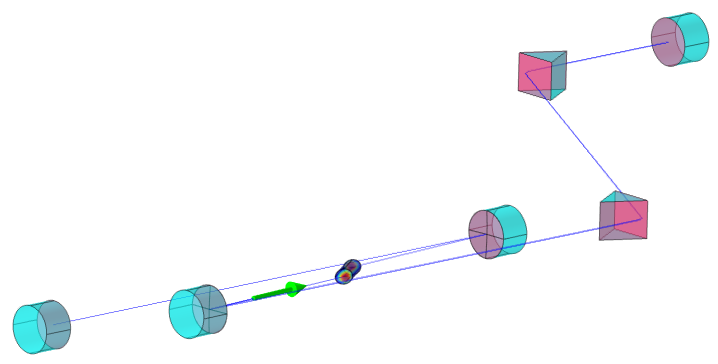
Ti：蓝宝石激光腔的稳定性分析模型，用于求解温度、力学位移以及射线位置和角度。

参考文献

1.  H. Kogelnik and T. Li, Applied Optics, Vol. 5, No. 10 (1966)
2. E. Hecht, Optics, Addison Wesley
3. W. Koechner, Solid-State Laser Engineering, Springer

其他资源

• 浏览这些激光腔教程模型：
  • 带有薄透镜的激光腔
  • 双镜腔
  • 蝴蝶结激光腔
• 在 COMSOL 博客 上了解有关激光模拟的更多信息：
  • 了解近轴高斯光束公式
  • 在 COMSOL Multiphysics 中模拟激光材料的相互作用