如何在 COMSOL Multiphysics® 中模拟不同类型的阻尼

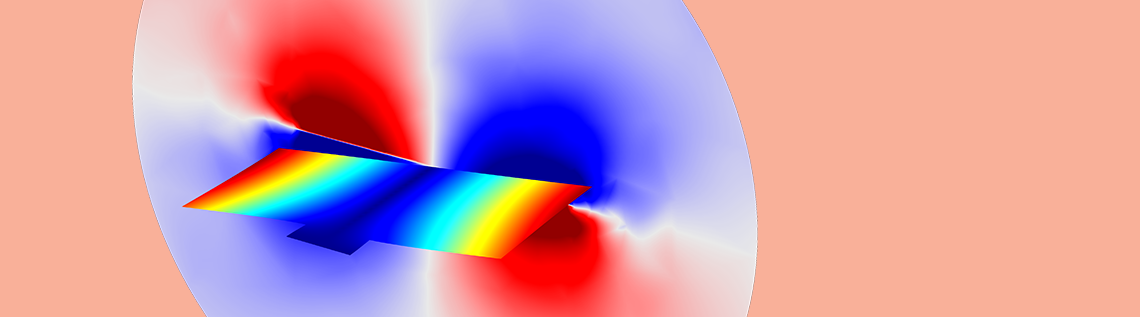
在之前的博客中，我们介绍了在结构中产生阻尼的各种物理现象，并讨论了如何用数学的方法表示阻尼。今天，我们继续研究如何在有限元模型中实际添加阻尼。

如何在有限元分析中添加阻尼

在进行结构动力学分析时，模拟阻尼可能是一项重要而困难的工作。

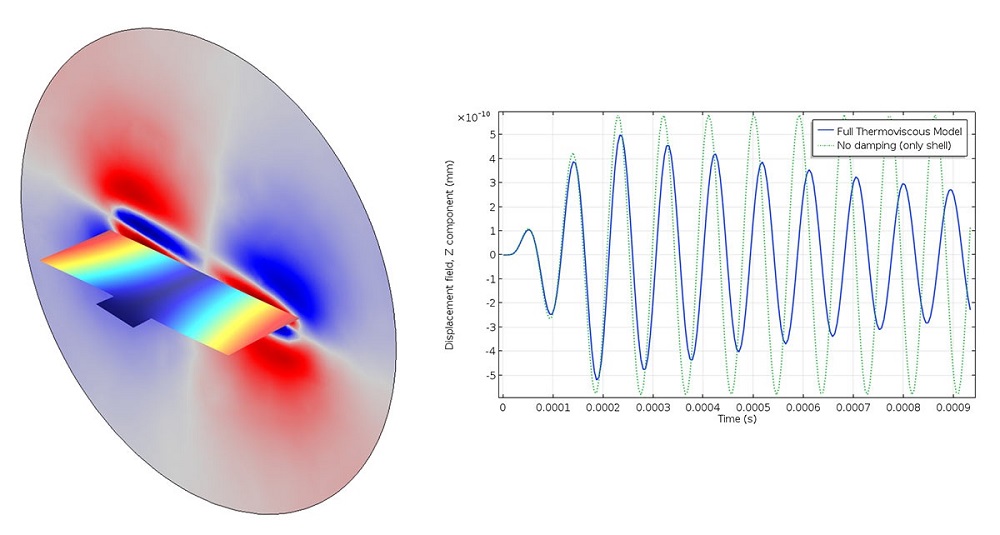
考虑了黏滞阻尼和热阻尼的振动声学微镜的瞬态分析。

接下来，我们将概述当使用 COMSOL Multiphysics^® 软件进行有限元分析和模拟阻尼效应时需要考虑什么因素。

特征频率分析

无论是否包括阻尼，特征频率问题在 COMSOL Multiphysics 中都可以被求解。模型中的任何损耗效应都会被考虑在内，并且计算出的特征频率为复数。这个过程在COMSOL中是自动运行的，我们无需在求解器中添加任何特殊设置。

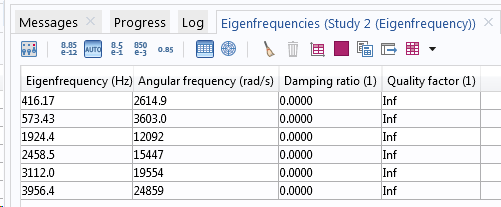
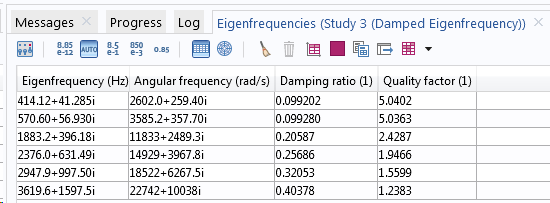
模型中不含阻尼（上表）和含阻尼（下表）时的特征频率。

大多数情况下，当包括阻尼时，特征频率和特征模都是复数值。复数模的振型是指在自由振动下，相角可提供有关结构中不同点之间的相移信息。也就是说，如果两个点的位移具有不同的相角，它们将不会同时达到峰值。

大多数情况下，阻尼对振型和特征频率的影响很小。在特征频率分析中包括阻尼的原因是需要估计各种谐振的衰减量。

频率响应分析

当激励频率位于固有频率附近（例如在 ±50％ 内）时，阻尼模型至关重要，如之前博客中的响应曲线所示。此时，我们必须选择合适的阻尼值。当接近共振频率时，结果完全受阻尼控制，因此，损耗系数选择 0.01 或 0.02，这表示最终的应力预测相差 2 倍。

时域分析

在时域分析中，除了模拟波传播或在施加载荷的过程中某些共振被强烈激发外，大多数情况下阻尼对结果产生的影响是有限的。

但是在时域分析中，阻尼还有一个重要作用：可以稳定时间步长。结构中经常会产生杂散的、微弱的波，除非适当地对其进行抑制，否则时间步长可能会变得非常小，而这并没有必要。为了抑制这样的波，在高频中引入阻尼模型是有好处的。

响应谱分析

在响应谱分析中，阻尼是设计响应谱的一部分，因此不应对其进行显式模拟。单个阻尼值可用于表示整个结构。

阻尼的数值模型

有限元公式

有限元离散运动方程的矩阵形式为

其中，M 是质量矩阵，C 是黏性阻尼矩阵，K 是刚度矩阵，u 是位移矢量，等号右边的 f 是力矢量。

在给定几何结构和基本材料参数（例如，质量密度和杨氏模量）的情况下，计算质量和刚度矩阵。阻尼矩阵具有多种不同的形式。不同类型的阻尼通常还可以进行组合。

在假定激励和响应为谐波的频域中，对应的方程为

式中，位移矢量和力矢量是复数值。

阻尼损耗因子

在频域分析中，阻尼损耗因子是描述材料损耗的主要方法。如上一篇博客所述，阻尼损耗因子的数学描述为复数值乘以刚度。

在 COMSOL Multiphysics 中，我们可以通过材料模型下的阻尼 子节点添加阻尼损耗因子。对于线性弹性材料，甚至可以为本构矩阵中的不同单元添加单独的损耗因子。

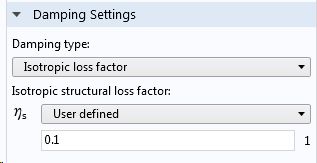
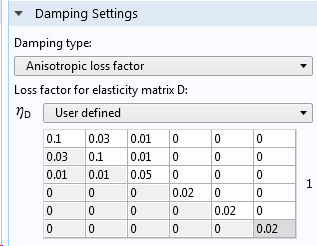
输入的阻尼损耗因子值。

实际上，损耗因子普遍具有一定的频率依赖性。在频率响应分析中，可以很容易地将损耗因子作为内置变量 freq 的函数。我们可以使用下面显示的表达式，也可以参考任何类型的频率函数。

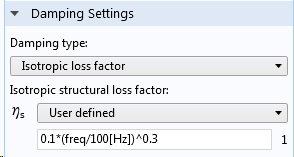
频率相关的损耗因子。

为了解损耗因子阻尼如何进入方程式系统，我们假设使用了相同的损耗因子。因此，阻尼矩阵可以表示为

运动方程变为

黏滞阻尼

在黏滞阻尼模型中，固体材料中的应力与应变率成正比。在最一般的情况下，将应力和应变率相关联的本构张量包含 21 个独立的常数。由于阻尼难以测量和量化，我们几乎无法得知它的数值，因此我们更常使用各向同性黏滞阻尼模型。

在 COMSOL Multiphysics 固体力学 接口中，黏滞阻尼使用两个常数表示：

• 本体黏度，\eta_b
• 剪切黏度，\eta_v

前者具有一个与体积变化成正比的阻尼，后者具有一个与振型变化成正比的阻尼。

黏性应力张量可以写成

式中，\epsilon_v 是体积应变，{\boldsymbol \epsilon}_d 是应变张量的偏差部分。

由于阻尼应力与应变率成正比，因此在较高的频率下它将更加明显。

黏滞阻尼是阻尼 节点中的另一个选项。

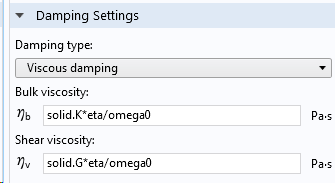
输入的黏滞阻尼。

黏滞阻尼可用于任何动态研究类型。

瑞利阻尼

作为质量和刚度矩阵的纯线性组合，瑞利阻尼是生成一个阻尼矩阵的简单方法，

该阻尼模型与物理阻尼过程没有直接联系。引入它是因为它提供了一个阻尼矩阵，该矩阵可以被来自无阻尼特征频率问题的特征模对角化，从而在不同模之间实现完全的动态解耦。

但是，刚度矩阵项（β阻尼）也可以看作与应变率成正比。实际上，纯 β 阻尼与黏滞阻尼有关

其中，K 和G 分别为弹性体积模量和剪切模量。

与黏滞阻尼一样，β阻尼在频率较高时阻尼更大。相反，在低频时，质量比例项α的阻尼很大。由于它作用于结构的速度，因此会抑制刚体运动。

材料模型中的阻尼子节点中也包括了瑞利阻尼。这样我们可以自由地创建阻尼类型（包含所有的瑞利阻尼）。为了使阻尼矩阵在系统水平上是质量矩阵和阻尼矩阵的线性组合，在所有阻尼 节点中，瑞利阻尼参数必须相同。如果不相同，则该特性仅在单元水平是正确的。

我们可以通过两种方式添加瑞利阻尼参数，既可以直接输入 α 和 β，也可以通过两种不同频率的阻尼比来添加。

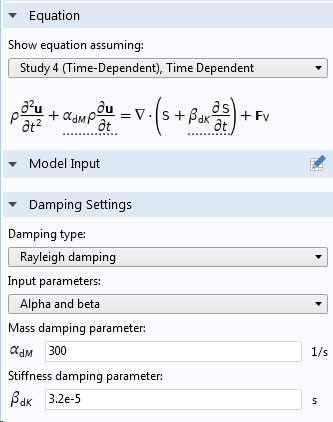
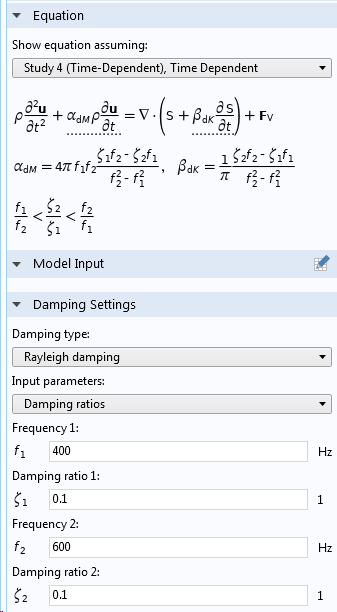
在材料模型的阻尼子节点中输入瑞利阻尼。

耗散材料模型

一些材料模型包括固有耗散，其中最有趣的可能是黏弹性模型。使用这种材料模型时，通常会有很大的阻尼。大多数情况下，我们不会将其与同一域上的阻尼节点结合使用。

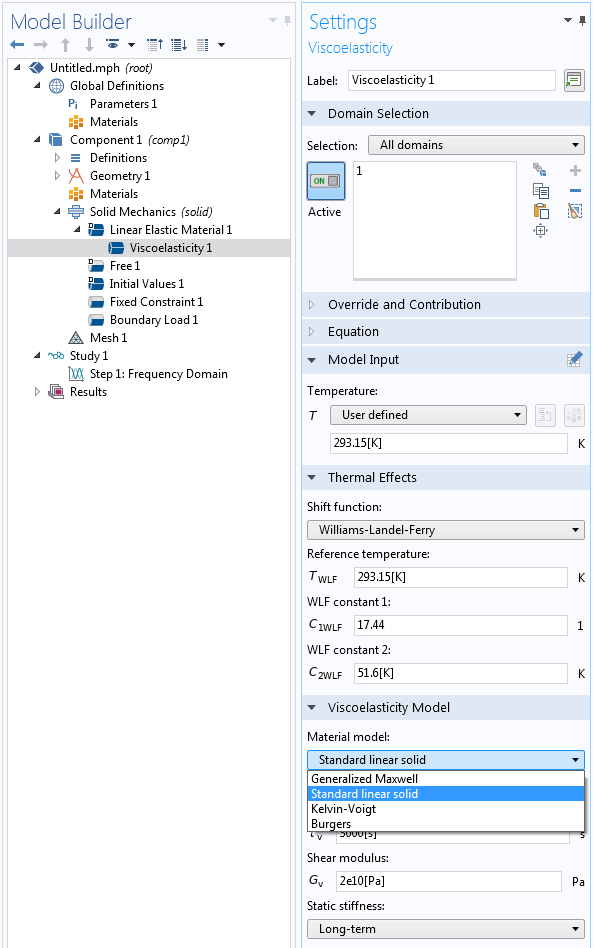
选择一个黏弹性材料模型。

热弹性阻尼

通过热膨胀 多物理场耦合中的设置，可以将热弹性阻尼直接引入模型中。

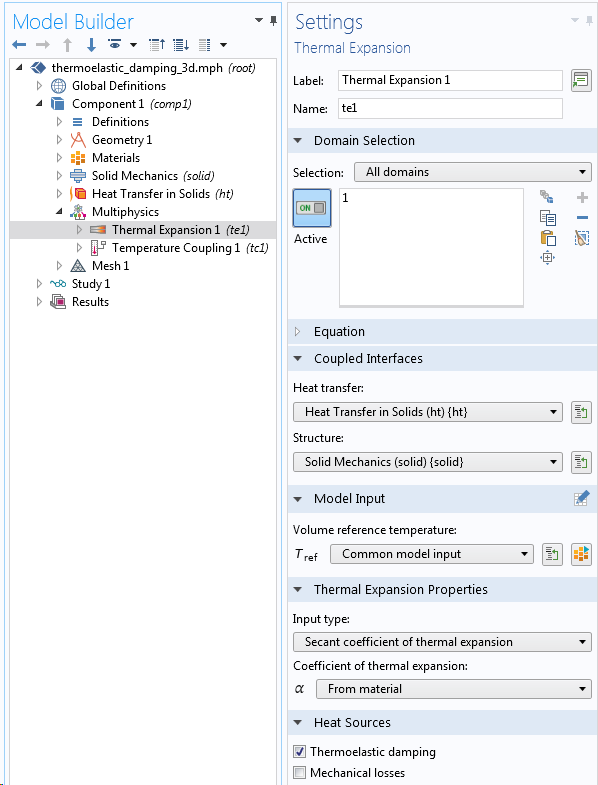
传热和结构耦合分析中的热弹性阻尼。

引入热弹性阻尼可以将与应力变化率成正比的热源项添加到热平衡方程中，即

式中，T 是温度，\boldsymbol \sigma 是应力张量， \boldsymbol \alpha 是热膨胀张量系数。

模态阻尼

模态叠加是求解线性结构动力学问题的一种非常高效的方法。将模态叠加与阻尼一起使用时，需要注意一些事项。

首先，应使用无阻尼问题进行初始特征频率分析，然后仅在模态叠加步骤中添加阻尼。确保这一点的最简便方法是在每个研究步骤中的物理场和变量选择部分进行设置。

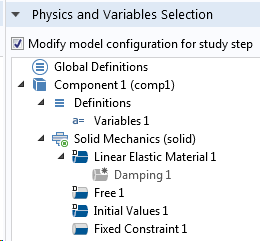
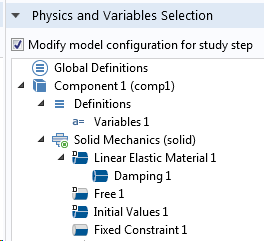
特征频率研究（左）和后续模态叠加研究（右）的研究步骤设置。

模态叠加允许所有类型的阻尼贡献，这并不夸张。在 COMSOL Multiphysics 的模态求解器中，并没有假定特征模解耦。这意味着与许多其他模态叠加方法相比，我们可以在COMSOL中求解更大范围的阻尼问题。

除了各种物理特性提供的阻尼之外，我们还可以为每个特征模提供阻尼比，即所谓的模态阻尼。如果我们从经验中得知某些模态的阻尼比其他模态更大，那么模态阻尼特别有用。当不同的物理现象被连接到振型时，就属于这种情况。可以直接在模态求解器的设置中设定模态阻尼。

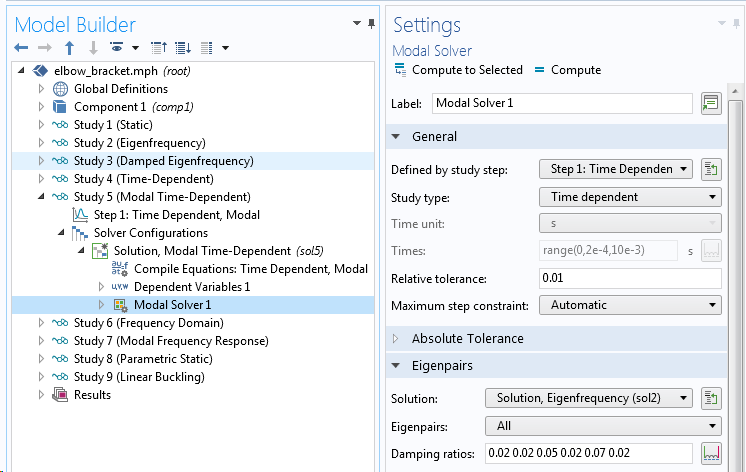
输入模态阻尼。

模态阻尼可以被添加到任何其他阻尼的贡献中。

无限边界条件

当需要模拟由于声发射或锚固耗散引起的耗散时，为模型设置边界条件非常重要。该边界条件允许射出的波消失而没有反射。COMSOL Multiphysics 在此处提供了多个选项，具体取决于所涉及的物理场接口以及分析是在时域还是在频域。

在频域中，完美匹配层（PML）可以表示边界条件趋向无穷远。完美匹配层公式从根本上衰减了输出波，因此反射的能量非常小，它可用于许多不同的物理场接口。由于输出波中的能量会丢失，因此在分析中将存在阻尼。

完美匹配层是使用计算域外部的少量单元层模拟的。

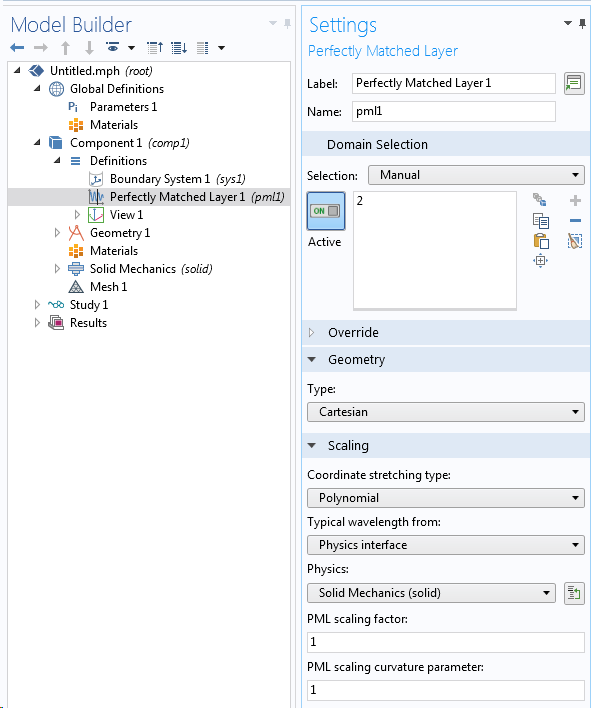
将域定义为完美匹配层。

固体力学 接口提供了一种特殊的边界条件，称为低反射边界。它的作用与完美匹配层相同：避免波反射。当波以倾斜角度入射到边界时，使用低反射边界节点的效果不如 完美匹配层，但它具有两个优点：

• 可用于时域分析
• 由于这是一个边界条件，因此不需要在计算域之外对额外的域进行网格剖分

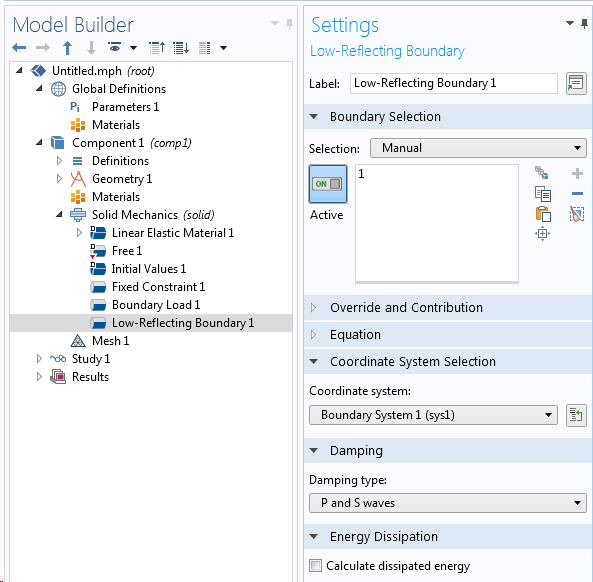
低反射边界节点。

模拟波向无穷远传播的另一种方法是使用声波的边界元方法（BEM）公式。

滑动表面之间的摩擦

如果摩擦是阻尼的重要来源，通常我们将不得不进行一些工程上的近似计算。理论上，我们可以通过模拟包括摩擦在内的完全接触来求解瞬态的问题。然而，在大多数情况下，这非常耗费计算机资源。

我们可以使用弹性薄层代替接触区，并为其配备黏性或阻尼损耗因子。然而，问题是如何估计剪切刚度和相应的损耗因子。估计这些参数的通用方法目前还在研究，我们可能必须对关节进行初步的局部分析来了解其特性。

使用其他功能添加阻尼

除了材料模型外，还有许多其他功能可以为模型添加阻尼。例如：

• 弹簧基座 功能
• 弹性薄层 功能
• 弹簧阻尼器 功能
• 多体动力学 接口中的关节和齿轮
• 集总机械系统 接口中的阻尼器 和阻抗 功能
• 转子动力学 和多体动力学 接口中的轴承
• 与速度有关的任意载荷
• 材料数据的复数值

结语

在结构动力学仿真中，模拟阻尼是定义模型必不可少的部分。COMSOL Multiphysics 提供了多种描述阻尼的方法。但是，结构中材料和组件的正确数据往往较难获取。

下一步

结构力学模块提供了特定的功能和特征，可用于模拟阻尼，单击下方按钮，了解结构力学模块：

• 阅读系列博客的第1部分：结构动力学中的阻尼：理论和来源
• 如果您对模拟阻尼感兴趣，可以在COMSOL案例下载中查找相关示例，这些示例中使用了不同的方法：
  • 弯头支架各项分析
  • 黏弹性结构阻尼器—瞬态分析
  • 支架—瞬态分析（bracket_frequency.mph）
  • 岩层中的爆炸波传播
  • Tonpilz 型压电换能器
  • MEMS 谐振器的热弹性阻尼
  • 盘式谐振器的锚损失
  • 受黏滞阻尼和热阻尼作用的振动微镜：瞬态特性