如何使用 COMSOL Multiphysics® 模拟关节中的流体摩擦

在各种各样机械设备中，会使用一些部件在相对运动的固体零件之间传递载荷，例如发动机、泵和涡轮等。常见的部件有活塞环、凸轮、齿轮齿和轴承。通常，通过在两个固体零件之间注入润滑油并在组件之间保持一层油膜，可以最大程度地减少摩擦和磨损。在本篇博客文章中，我们介绍了使用 COMSOL Multiphysics^® 多物理场仿真软件对润滑关节中的流体摩擦进行建模的方法。

润滑方式

根据两个接触面之间的载荷及其几何形状的不同，有以下几种润滑方式：

• 液膜润滑
  • 载荷由液膜完全支撑，从而使接触表面被液膜完全分开
• 弹性流体动力润滑
  • 存在于不一致表面之间或具有高载荷条件，物体在接触时承受很大的弹性应变
  • 由于表面之间相对运动的泵吸作用，可以维持变形表面之间流体膜的存在
• 边界润滑
  • 物体在粗糙处紧密接触，流体润滑效应可忽略不计
• 混合润滑
  • 全膜弹性流体动力润滑和边界润滑之间的一种状态，仅保持润滑膜不足以完全分离物体
  • 流体力学效应相当重要

本文我们将重点介绍全膜润滑方式，在这种情况下，由于关节内形成了一致的表面并且压力不够高，所以不会引起明显的变形。

计算润滑剂分隔平板之间的黏性阻力

下图为两个由润滑剂隔开的平板。底板保持固定，顶面以水平速度 U 移动。

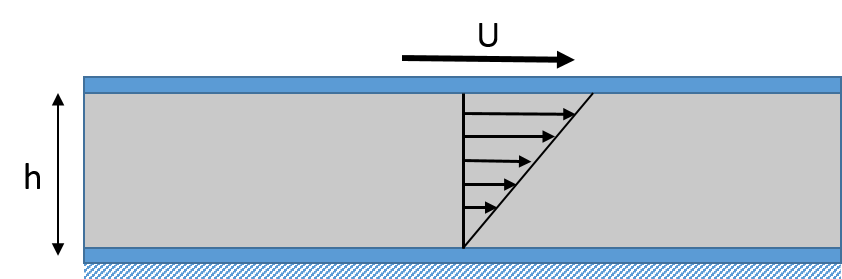
两个平板之间的剪切流。

对于没有压力梯度的库埃特流（Couette flow），润滑剂在厚度方向z上的速度分布表示为：

 
因此，润滑剂中的黏性剪切应力为：

 
上式与厚度坐标无关。

顶板上的黏性剪切阻力为：

 
其中，A是平板的面积。

在关节中，由于薄膜厚度发生变化，润滑流体也存在压力梯度，因此，速度分布将变为：

 
其中，x是沿流动方向的坐标。

此时，顶板上的黏性剪切应力与黏性剪切阻力相同，分别为：

黏性剪切应力：

黏性剪切阻力：

确定润滑关节中的黏性力

下面，我们以铰链关节为例来说明关节中的黏性力。铰链关节是由两个相对旋转运动的部件组成的关节，其中旋转轴为关节的轴。通常，与上述示例相反，形成铰链关节的两个部件都可以运动，因此可以使两个部件处于运动状态。例如，往复式发动机的连杆和曲柄销之间的关节。如下图所示，一般情况下，铰链关节部件分别以速度 Ω₁ 和 Ω₂ 绕它们的中心旋转。

如果部件1 的内半径 R₁，部件 2 的外半径是R₂，则表面分别以速度 Ω₁R₁ 和 Ω₂R₂ 移动。

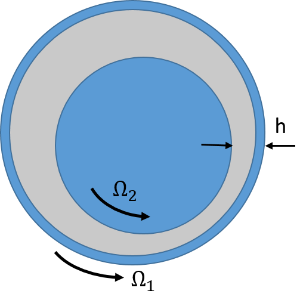
润滑铰链关节。

在局部的任何位置，流量都与上述平板的流量相似。因此，薄膜在切线方向上任何圆周位置的速度分布可由下式计算：

 
式中，下标 t 表示切向分量，z 由分量 2 测量。

润滑剂中的黏性剪切应力为：

 
假设 Ω₁R₁ > Ω₂R₂，表面1 中的剪切应力为：

 
表面 2 中的剪切应力为：

 
然后，通过对表面上的剪应力积分，得出两个表面上的总阻力：

在 COMSOL Multiphysics^® 中对润滑关节进行建模

COMSOL Multiphysics®软件的多体动力学模块 和结构力学模块中包含许多关节。这些关节可以是刚性关节也可以是柔性关节。顾名思义，除关节的自由度（DOF）外，刚性关节不允许关节之间存在任何相对运动。而在柔性关节中，除关节的自由度（DOF）外，可以为相对运动指定零部件之间的刚度。这种刚度可能是由于组件本身的柔韧性，形成关节的区域之间存在液膜或两者的结合所致。本节，我们主要讨论液膜的影响。

关节中的润滑剂通过液膜压力支撑关节力，从而避免结构间的接触并减少关节组件之间的摩擦。尽管没有接触摩擦力大，但是由于关节的相对运动而引起的润滑剂剪切力阻碍了形成关节的两个部件的相对运动。这种阻力就是我们所说的关节中的流体摩擦力。因此，关节中的液膜会在关节部件上施加两种类型的力：

1. 支撑关节上载荷的力
2. 阻碍组件相对运动的黏性剪切力

因此，计算液膜支撑力的最简单方法是将液膜的动态特性（刚度和阻尼系数）作为弹性关节中的关节刚度和黏性阻尼。通常，这些特征可以通过一些实验获得。对于简单的情况，也可以将解析表达式作为离心率的函数计算轴承的动态特性。COMSOL Multiphysics 还提供了一种通过液体动压轴承 接口计算关节中润滑膜动态特性的方法。该接口内置于转子动力学模块中（COMSOL Multiphysics 和结构力学模块的附加组件，用于模拟液膜轴承中的流动。另外，要考虑黏性阻力，应将关节力（或力矩）施加到关节中的相对运动。在上一节 ,我们介绍了计算黏性阻力的方法。

计算每个关节的动态系数和黏性阻力并将其用于多体仿真中可能是一个相当繁琐的过程。COMSOL^® 软件提供了有一种更简单的模拟关节润滑的方法。借助软件的实体–轴承耦合多物理场耦合功能，可以将液体动压轴承模拟与多体和结构力学模拟直接结合起来。该多物理场耦合功能将结构的运动传递到液体动压轴承接口，以计算液膜厚度的变化对液膜中压力分布的影响。然后，液膜中的压力和剪切力作为外力传递回结构，使其成为双向耦合。

关节中的流体摩擦建模示例

为了理解上文解释的建模过程，我们以一个往复式发动机的活塞和气缸建模为例进行说明。如下图所示，活塞和气缸的壁被一层薄润滑膜隔开。

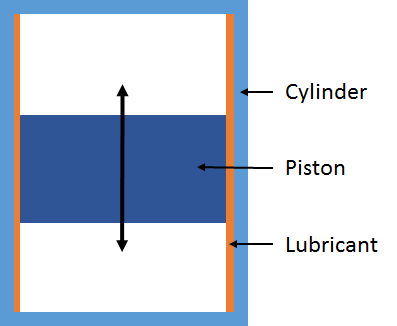
气缸中往复运动的活塞的润滑。

活塞连接到连杆，连杆的另一端连接到曲柄销。整个系统的原理图如下图所示：

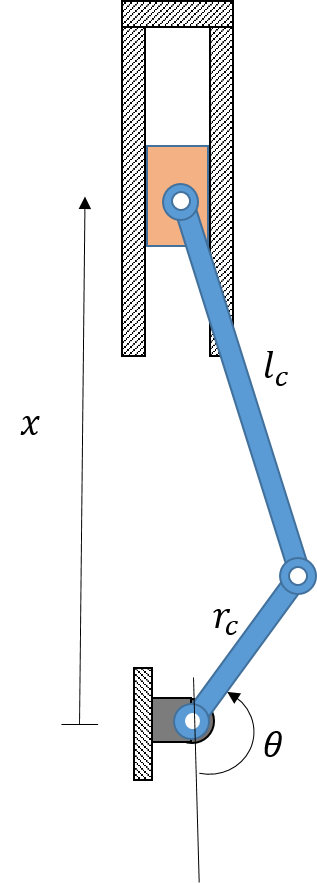
曲柄滑块系统示意图。

曲柄的半径为 r_c，以角速度 Ω 旋转。连杆的长度为 l_c。从几何的角度考虑，曲柄中心活塞的垂直位置由下式计算：

 
式中，θ=Ωt。

在上述表达式中，θ 表示基于活塞位于下止点（BDC）的曲柄位置（角度）。

曲柄中心活塞的初始位置（在 BDC 处）为

 
因此，活塞的垂直位移由下式计算：

 
请注意，在 t=0 时，活塞的位移和速度均为 0。

进一步假设由气压引起的垂直力作用在活塞上，可由下式计算

 
因此，当活塞位于下止点时，垂直力为零；当活塞位于上止点时，垂直力最大。实际情况中，该垂直力对 θ 的依赖性更大。连杆通过其在活塞上的反作用力来支撑此载荷。有趣的是，该反作用力 F_c 始终沿着连杆的长度，如下图所示。

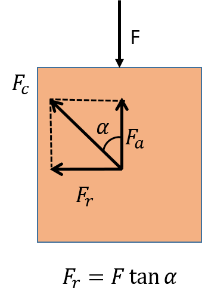
活塞的自由体受力图。

因此，反作用力的垂直分量 F_a 支撑活塞上的气压。但是，还有一个附加的水平分量 F_r 作用在活塞上，它将活塞推至气缸壁，该力的大小由下式计算

 
当活塞在气缸中移动时，也需要将其施加在活塞上。

为了模拟此类问题，首先创建活塞的几何形状。我们可以使用固体力学接口中的线性弹性材料模型来模拟活塞的弹性。活塞的运动可通过刚性连接件功能规定，也可在固体力学接口中使用该功能。通过建立上述几何模型，规定了活塞在垂直方向（z方向）上的运动。同样，活塞不能绕其轴线旋转（z轴）。活塞的横向平移和倾斜可以通过活塞上的力平衡来自由设置。我们可以通过 刚性连接件 功能的设置来指定这些条件，如下图所示。

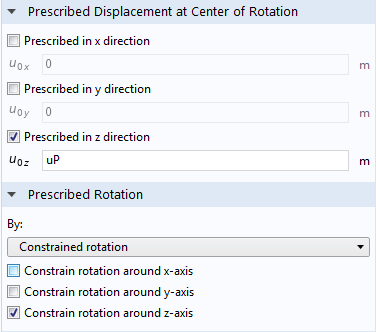
屏幕截图显示了活塞的规定运动和位移。

使用刚性连接件 功能下的作用力”子功能模拟连杆施加到活塞上的水平载荷。

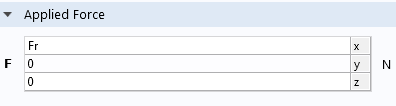
屏幕截图显示了作用力功能及其设置。

计算活塞上的流体摩擦需要先获取从润滑膜到活塞运动的阻力。尽管我们可以一起模拟气缸和活塞（以及它们之间的润滑剂），但是由于气缸处于静止状态，因此不必建模。可以在流体动压轴承 接口中直接指定气缸的静止状态。

活塞的横向运动会导致活塞和气缸之间的间隙发生变化，使润滑剂的厚度改变。因此，润滑膜中的压力分布还取决于接触边界的相对运动。在高载荷条件下，活塞变形也会改变薄膜厚度。如果薄膜中的压力与接触边界的有效刚度之比较小，则可以忽略接触期间的变形。否则，需要考虑接触边界的变形，因为它在确定接触边界之间的有效摩擦方面起着重要作用。这类模拟被归类为弹性流体力学（EHD）模拟。在这种情况下，由于期望压力水平低，因此膜厚度将很大程度上受活塞的横向运动而不是其变形的影响。

为了对润滑膜建模，我们对纳维-斯托克斯和连续性方程进行了薄膜近似，得到雷诺方程，该方程是在流体表面而不是在流体域上求解。流体动压轴承 接口可以求解雷诺方程，并可用于获取活塞表面上膜中的压力分布。建立润滑膜模型需要的参数包括：初始膜厚度、润滑剂的黏度和密度，以及接触边界的运动。所有这些信息可以通过流体动压轴承 接口的流体动力轴颈轴承 功能指定。

请注意，一般来说，液体动压轴颈轴承 功能可以模拟轴颈轴承，其中轴颈除了其平移运动外还进行了轴向旋转。此功能也可用于轴颈无轴向旋转的情况，例如本模型中的活塞。使用内置的实体–轴承耦合 多物理场功能，可以轻松地将接触边界的运动转移至液体动压轴颈轴承 功能。如前所述，此功能会自动在结构边界上施加由薄膜中润滑剂的压力和剪切力。

查看仿真结果

下面的动画显示了零件进行往复运动时薄膜中的压力分布和活塞中的应力。为了突出活塞的横向运动，抑制了活塞的往复运动。

活塞中的 von Mises 应力（左）和薄膜中的压力（右）。

在活塞运动半个周期后，我们可以看到应力的变化。请注意，在上行行程中，随着连杆在右侧壁上推动活塞，活塞右侧的压力增加而在左侧减小。在下行行程中，情况正好相反。

下图给出了在垂直方向上作用在活塞上的润滑膜剪切力随时间的变化。

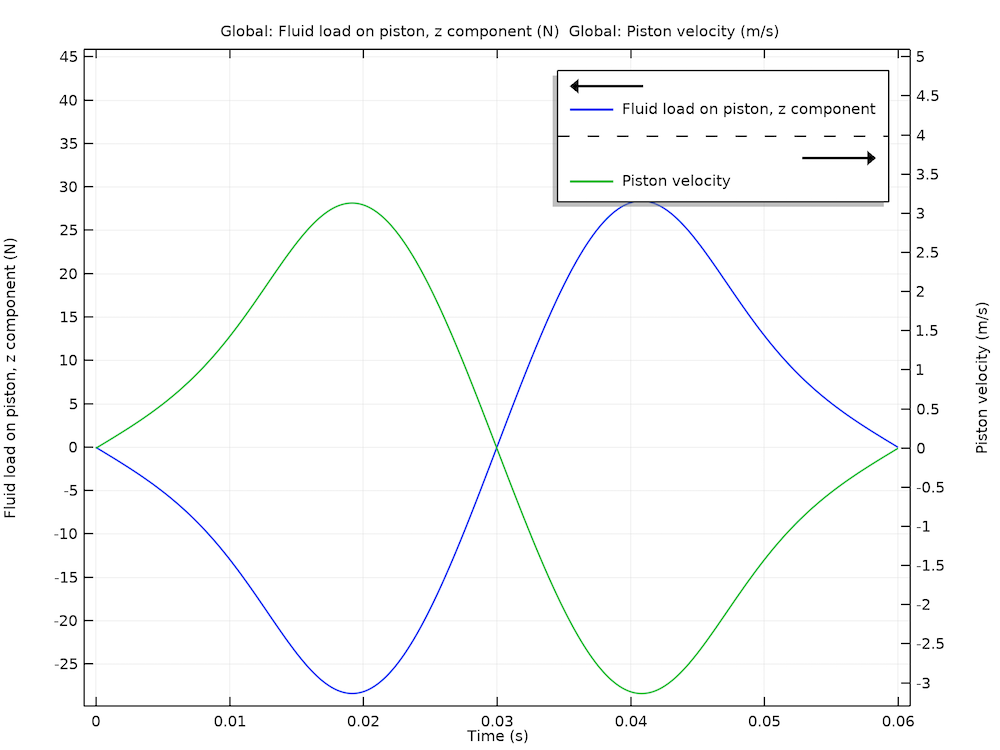
活塞速度和黏性力。

请注意，作用在活塞上的黏性力始终与其速度相反。黏性力系数（阻尼系数）为黏性力与活塞速度之比，此例中约为 8N*s/m。

往复式发动机模型案例

下面，我们介绍 COMSOL 应用程序库中使用转子动力学 模块进行建模的 采用液体动压轴承的往复式发动机 模型案例。该示例演示了将结构或多体仿真与流体动力轴承相结合进行建模的步骤。此示例中模拟的是通过基座上的动压轴颈轴承支撑的单缸往复式发动机。当在活塞上施加气压时，分析各种发动机组件的动力。在发动机运转期间，活塞上的载荷通过连杆、曲柄和轴承传递到基座上。

模型通过分析轴承中的压力和基座中的应力，了解一个操作周期内的轴承性能和基座上的应力变化。此外，还分析了曲轴中的应力。下面的动画显示了曲轴和基座上的应力变化，以及在其运行过程中产生的轴承压力分布。在施加气压后，活塞在下行行程期间的轴承压力最高。

往复式发动机：曲轴和基座上的应力以及轴承上的压力。

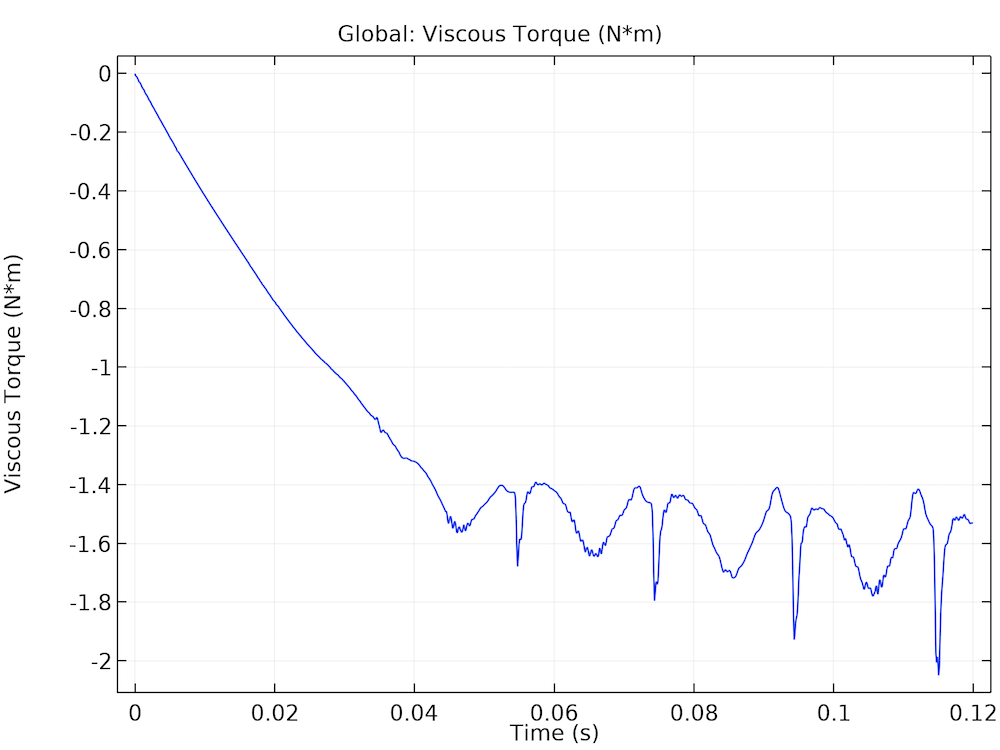
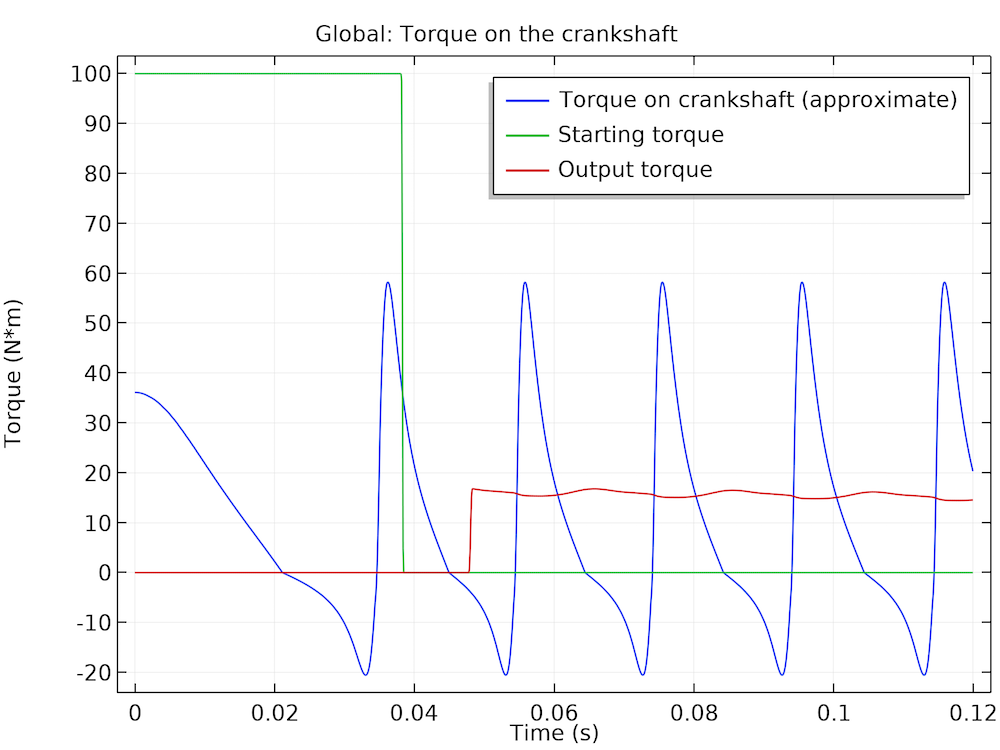
下图绘制了在不同操作周期下轴承上的黏性扭矩。当活塞到达上止点时，气缸压力最高。此时，轴承中的压力也很高，轴颈的偏心度最大。这将在轴颈上产生高摩擦，在黏性扭矩图中显示为尖锐的负峰。请注意，黏性扭矩约为载荷扭矩的10％（约 16Nm），因此，在计算发动机损失时不能忽略。

轴承中的黏性扭矩（左）以及曲轴上的驱动扭矩和载荷扭矩（右）。

下一步

单击下面的按钮，了解更多有关在转子动力学模块中用于模拟薄膜润滑剂流体特征的特殊功能。

 
请注意，转子动力学模块（以及多体动力学模块）是结构力学模块和 COMSOL Multiphysics 的附加产品。

延展阅读

• 在COMSOL 博客上了解有关轴承建模的更多信息：
  • 如何在 COMSOL Multiphysics® 中对滚动轴承建模
  • 使用转子轴承系统模拟器分析临界转速