
许多细长结构可以使用二维横截面进行有效建模。一个典型的假设是平面应变近似,它意味着所有平面应变分量都是零。这种假设适用于面外变形被抑制的情况,例如固定结构的末端。然而,在许多情况下,结构会在面外方向上自由扩展。让我们来讨论如何对这种有时被称为广义平面应变的情况进行建模。
利用平面应变、平面应力和广义平面应变条件
在平面应变条件下,物体不能在面外方向上扩展。在此方向上,通常存在由非零泊松比引起的面内应变耦合应力。另一方面,当研究薄板时,平面应力假设更加实用。在这种情况下,材料在面外方向上自由收缩或膨胀,横向应力为零。
如果与面内尺寸相比,结构在横向上很长,但在横向上仍不受约束,那么上述假设都不适用。这时我们可以采用广义平面应变条件。
广义平面应变状态公式
平面应变公式的一种可能的推广是假设应变独立于面外坐标。在 COMSOL Multiphysics® 软件中,可以借助截面的二维几何图形和固体力学 接口来实现这个假设,其中平面应变公式是默认选项。
假定应变张量的分量仅仅是面内坐标 x 和 y 的函数(可能是时间):
(1)
在小应变的假设前提下,应变张量的分量与位移场相关:
(2)
上述方程有下列三维解:
(3)
{u\left( {x,y} \right) – \frac{{a{z^2}}}{2}} \\
\\
{v\left( {x,y} \right) – \frac{{b{z^2}}}{2}} \\
\\
{\left( {ax + by + c} \right)z} \\
\end{array}} \right]
其中 a、b 和 c 是常数系数。
相应的平面应变是:
(4)
{\varepsilon _{zz}} = ax + by + c \\
{\varepsilon _{xz}} = {\varepsilon _{yz}} = 0 \\
\end{array}\]
这种应变状态不同于标准平面应变假设,原因在于法向面外应变非零,在横截面上做线性变化。在截面 z = 0 时,变形位于平面内,并且通过面内位移分量 u(x,y) 和 v(x,y) 进行充分表征。
法向面外应变表达式中的系数 a、b 和 c 可作为额外的自由度(DOF)引入到整个模型中(全局变量)。我们可以使用结构力学 接口提供的外部应变 特征来引入额外的应变贡献。
当分析应力光学效应时,比如由几层不同的材料组成的双折射波导(如绝缘体上硅波导),广义应变公式非常重要。应力光学效应教程模型展示了这种情况。
广义平面应变公式的应用实例
为了说明这种方法的效率,我们考虑一个简单的梁状结构,它由两个拥有方形横截面的 1 cm 层组成。这些层由弹性和热性能差别极大的材料制成的:铝和尼龙。数据来自 COMSOL Multiphysics 软件内置的“材料库”。面外 z 方向上的长度 L = 20 cm。假定该结构是在高温下制造的。由于材料的热膨胀性能不一致,当冷却到工作温度时,结构中会累积残余热应力。这使得结构在面外方向上轻微弯曲。
下图显示了一个总位移绘图,以及完整的三维模型和二维广义平面应变条件:
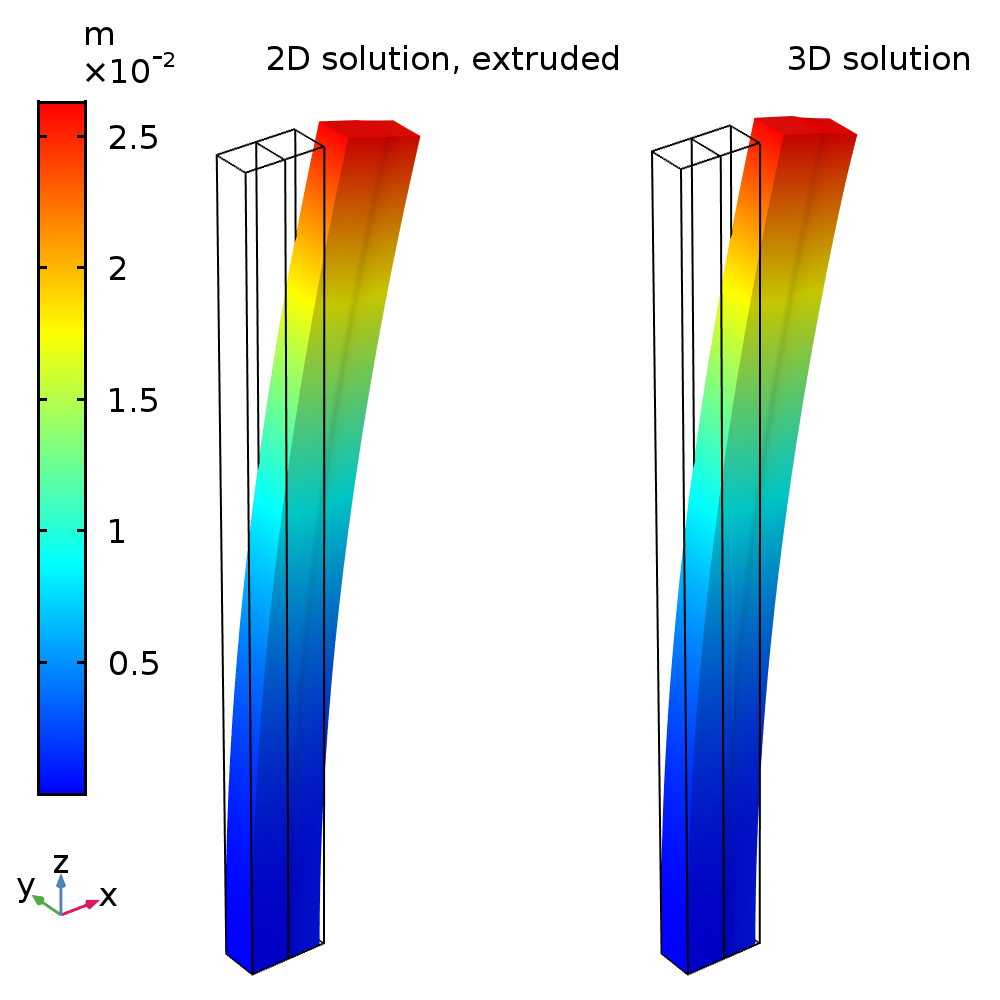
利用给定三维位移场的解析解,将横截面内 u(x,y) 和 v(x,y) 的二维解向面外 z 方向拉伸。
三维解需要约 32000 个自由度,而二维解大约只需要 250 个自由度。
下图显示沿其中一个边的面外应变和应力的变化。
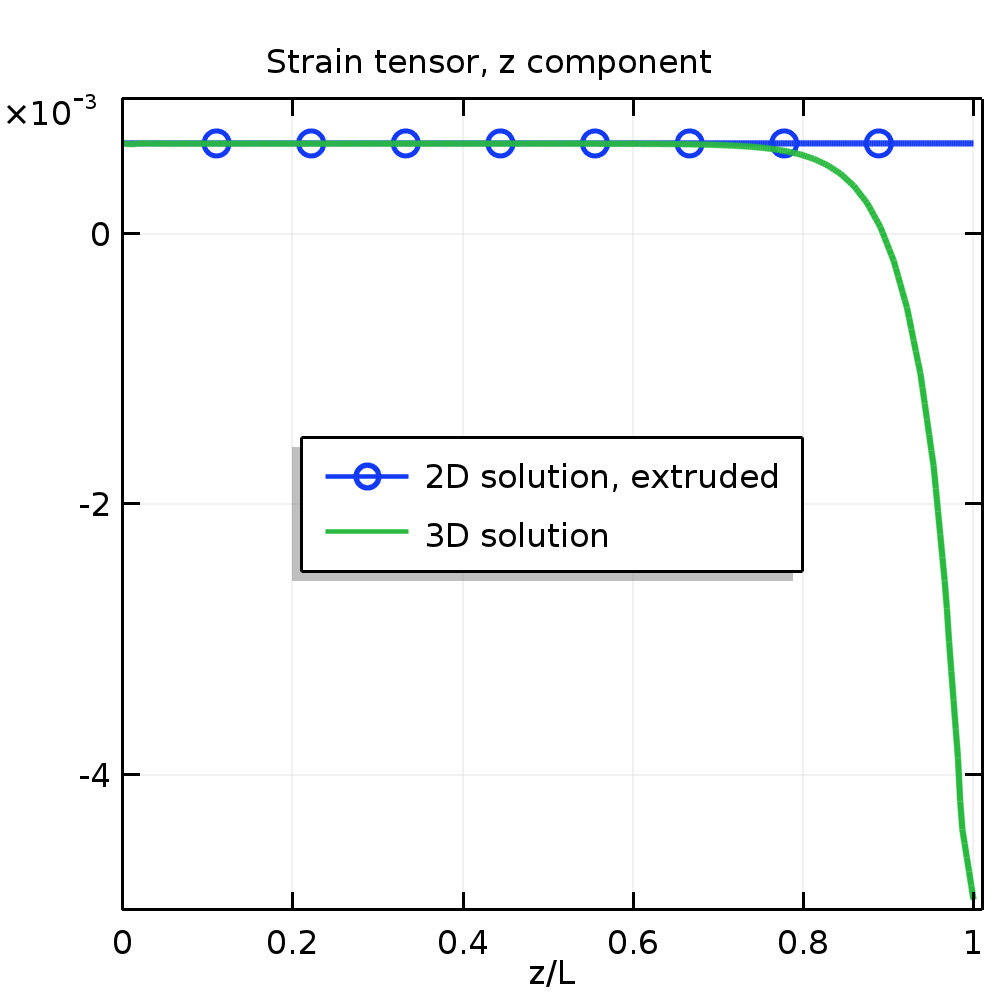
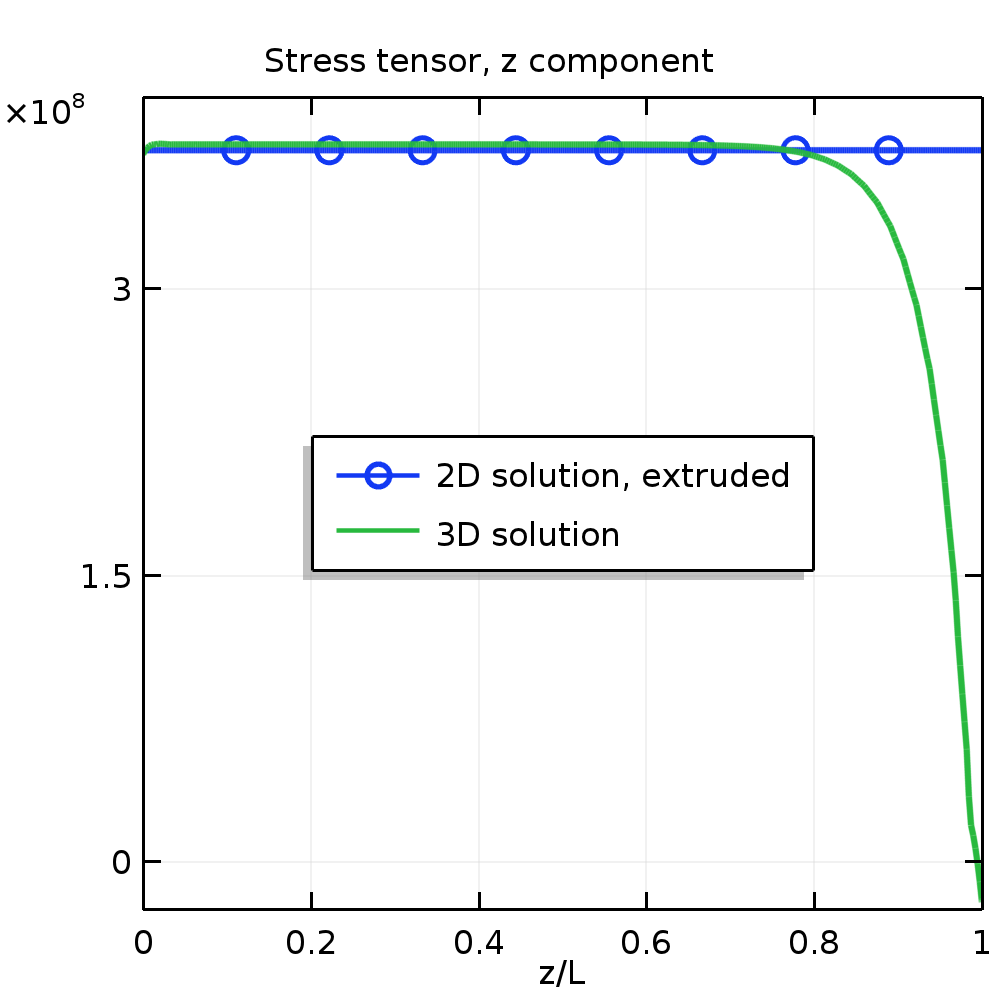
沿 z 轴的应变(左)和应力(右)。
大约 80% 真实三维结构中的应力和应变场与广义平面应变理论的预测相似。只有在应力趋于零的自由端附近,应变场开始偏离横截面内的线性分布。
在 COMSOL Multiphysics® 中添加广义平面应变条件
为了引入广义平面应变近似所需要的变化,一种方法的第一步是使用二维组件和固体力学 接口,然后在“模型开发器”树中添加以下节点:

“模型开发器”树,显示添加广义平面应变条件所需的节点。
除了二维问题的标准设置之外,您还必须执行以下步骤。首先,在全局方程 节点中,将 a、b 和 c 系数添加为自由度(DOF)。请注意,本文没有为这些变量设置任何方程。因此,除了变量名称以外,所有输入字段都保留默认值。
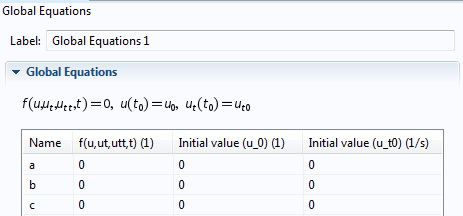
全局方程节点显示 a、b 和 c 系数。
在变量 节点中,根据 a、b 和 c 定义面外法向应变分量 eZ。
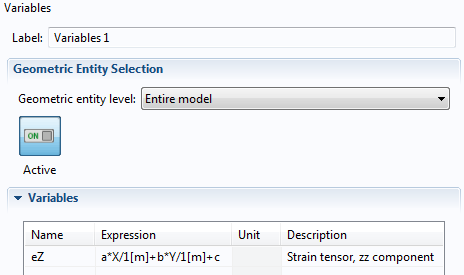
变量 节点,显示变量 eZ 的表达式。
其次,将额外的应变分量添加到外部应变 节点的应力-应变关系中。请注意,在使用 Hooke 定律计算弹性应力应变之前,您在此节点中输入的任何表达式都将从总应变中减去。通常,这个节点可以用来包含非弹性效应;例如由各种机电多物理效应引起的应变。在这里,我们只是将它作为一种机制来增加额外的平面应变分量,在平面应变公式中此分量默认为零。
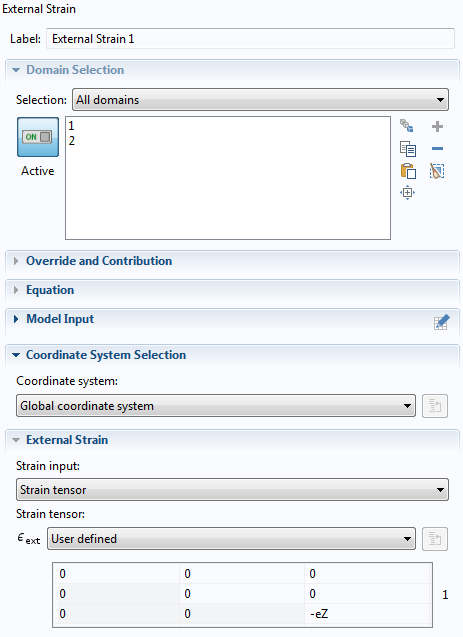
外部应变 节点,显示额外的应变分量。
最后,在弱贡献 节点中,添加由面外应力完成的额外的虚拟工作。由此建立了一个(弱贡献 形式)方程来确定 a、b 和 c,在这里,solid.d 是定义在固体力学 接口中的 z 方向的厚度。
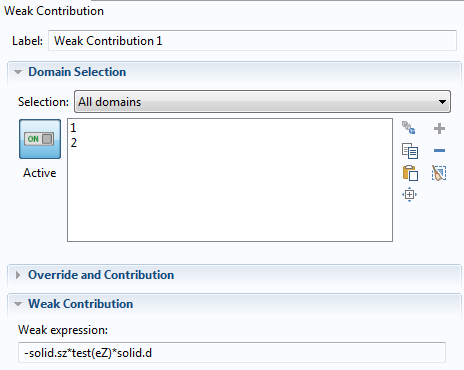
弱贡献节点,显示弱表达式。
替代方程
您也可以跳过上面的第三步和第四步,直接将应变变量 eZ 插入到线性弹性材料节点的方程中。为此,请确保已启用方程视图。
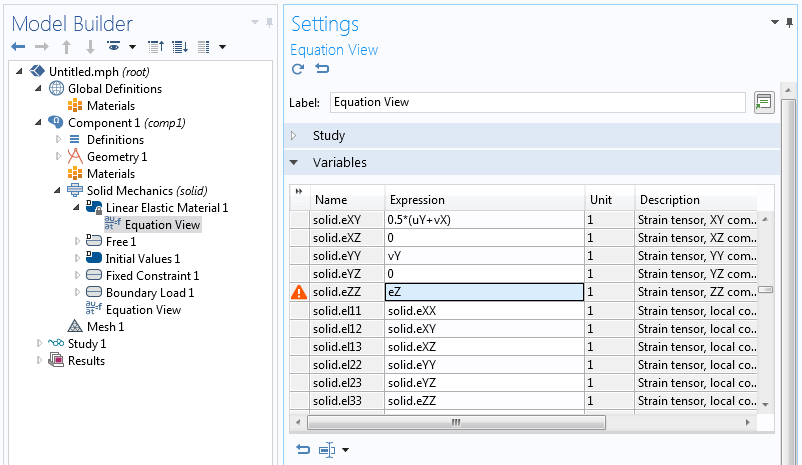
方程视图设置。
这样,z 方向的新应变直接变成材料模型的一部分,并且被添加到线弹性材料 节点所生成的弱表达式中。
结束语
我们在本文中展示了如何使用 COMSOL Multiphysics 建模功能来模拟面外方向上自由延伸的细长结构。通过使用二维广义平面应变近似,我们能够显著减少计算工作量,同时再现结构中可能发生的面外弯曲——这种三维效应在压电器件和光波导等应用中非常重要。我们也可以引入结构的面外剪切,这对于某些压电产品应用非常重要。
更多资源
- 在 COMSOL 博客了解更多结构力学建模:






评论 (4)
泽华 汪
2021-07-12问您一下,用PDE接口的话应变要怎么表示分量才可以使其是标量的。
Lei Cao
2021-07-13 COMSOL 员工泽华 汪, 您好!
建议您先学习下 PDE 建模的基本操作方法,再结合固体力学接口中的方程以及内置变量定义。PDE 相关视频资源如下:
http://cn.comsol.com/video/equation-based-modeling-webinar-cn
http://cn.comsol.com/video-training/advanced-skills-and-tricks-3
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
泽华 汪
2021-09-28您好,请问我做力学耦合,给一个预制裂纹,怎么设置断裂序参量的初始值可以使裂纹扩展的区域是0,完好的地方是1呀。
hao huang
2021-10-08 COMSOL 员工您好,建议您将您的模型以及问题详细描述一下发送给 COMSOL 技术支持邮箱: support@comsol.com