
今天,来自西班牙巴塞罗那自治大学(UAB)的特邀博主 F. Xavier Alvarez 将与我们一起探讨如何使用一种新的理论框架和 COMSOL Multiphysics® 软件结合来模拟纳米尺度上的传热。
随着电子工业的发展,电子器件被开发的越来越小。这些器件会产生热量,需要进行有效散热。以往的观察表明,在较小的尺度上,傅里叶定律有一定的局限性,难以准确预测这些热量。当前的主要研究是如何解决这个问题。
使用傅里叶定律描述热输运
1822 年,傅里叶出版了《热的解析理论》(Analytical Theory of Heat)。从那时起,傅里叶定律就被用于描述各种系统中的大量不同的实验观察,并且成果显著。傅里叶定律由热梯度与热通量的简单关系式来描述:
(1)
式中,\lambda为导热系数,是一种材料属性。
过去几十年的研究表明,使用方程(1)分析特征长度 L 小于热载体(声子)平均自由程的器件时得到的结果并不不准确。实际观察到的热流比傅里叶定律预测的要小得多,从而降低了这些组件释放多余热量的能力。这个问题常常通过一个有效的导热系数来解决,该系数取决于特征长度 \lambda (L),而特征长度必须根据经验确定。
我们能够通过动力学理论正确预测简单几何结构中的导热系数,但目前还无法将其应用在几何结构复杂的电子器件中。
动能集合模型简介
巴塞罗那自治大学开发的动能集合模型(kinetic-collective model, KCM)是一个主要描述纳米和微米尺度的热输运,以及通过微观计算方程来计算中相应输运参数的理论框架。通过这种计算组合就可以获得一种能够准确预测热输运的模型。
傅里叶定律的一阶修正为 Guyer-Krumhansl 方程:
(2)
将该方程与通量的边界条件结合,出于教学原因,这里我们使用最简单的形式:
(3)
请注意,方程(2) 中新增的拉普拉斯项将傅里叶定律转变为描述黏性流体的,类似斯托克斯方程的定律。因此,遵循 方程(2) 的特性通常被称为 声子流体动力学。这个新增项引入了一个热黏度,它降低了通量不均匀区域的有效热导率。在这些区域,热通量与温度梯度不再平行,从而对热和温度分布产生重要影响。
我们采用像纳米线这样的简单几何结构来分析方程(1)和方程(2-3)产生的不同结果。在下图中,可以看到半径为 500 nm 的纳米线内部的热流,其一端加热,另一端冷却。分别在导线的两端施加高温和低温,并为通量应用周期性条件,以避免边界对分布产生影响。
通过模拟从傅里叶定律(l=0)到 l = 300 nm 范围内黏度值增加的情况,我们绘制了热通量分布图。可以明显地观察到主要差异:方程(1)在纳米线横截面上给出了一个恒定的通量,而方程(2-3)给出了热流分布曲线。
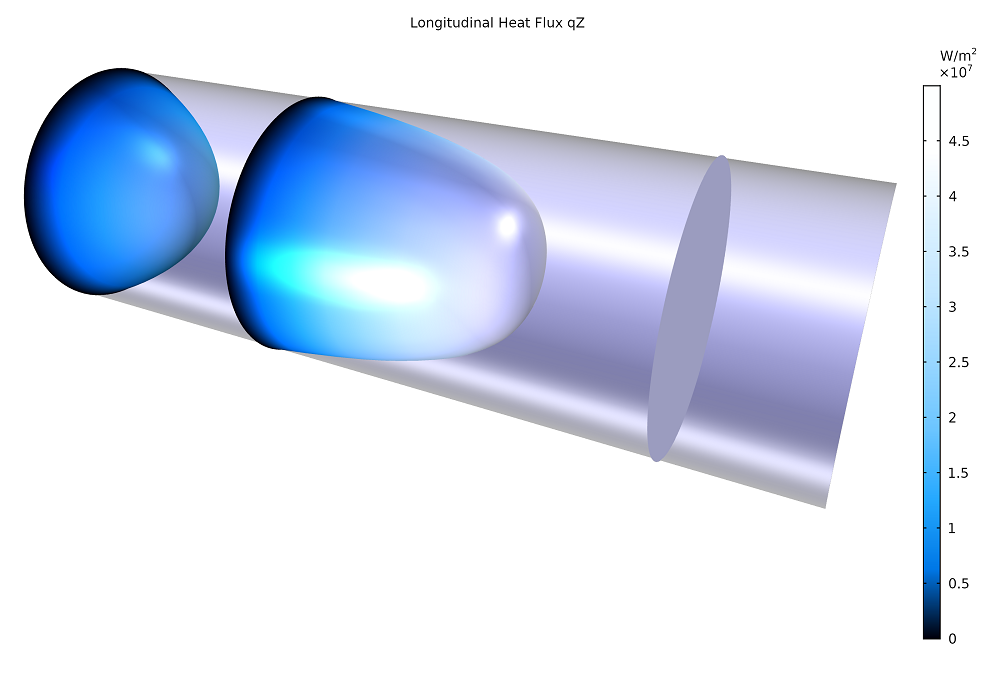
半径为 500nm 的纳米线内部的纵向热通量。三个剖面图依次显示了基于方程(2-3)得到的热通量分布。右边均匀温度分布的剖面对应于 l=0 (傅里叶定律),中间的剖面对应于 l=100nm,左边的剖面对应于 l = 300nm。总热通量随l 的增大而减少,导致纳米线的有效电导率降低。
出现热通量曲率是因为边界的影响减少了宽度为 l 的区域中的热流。当 l 小于线半径(l<R)时,仅边界附近得圆柱形外壳(即克努森层)内的热流受到影响。克努森层之外的区域则恢复到接近傅里叶极限的热流值。
当特征长度与纳米线半径相当时,克努特森层增厚,直至这种影响在中心位置也能观察到。此时,示例中纳米线横截面各处的热流都减小,并且热流剖面与黏性流体的抛物线泊肃叶(Poiseuille)流动相似。
如前文所述,确定纳米线中热输运方程的最重要是,无法通过实验获得横截面内的热通量分布。唯一可以测量的是有效热导率,其定义为横截面上的平均通量除以温度梯度。这使我们无法从实验中区分观察到的现象是根据 Guyer-Krumhansl 方程预测的,还是仅根据有效热导率减小的方程(1)预测的。
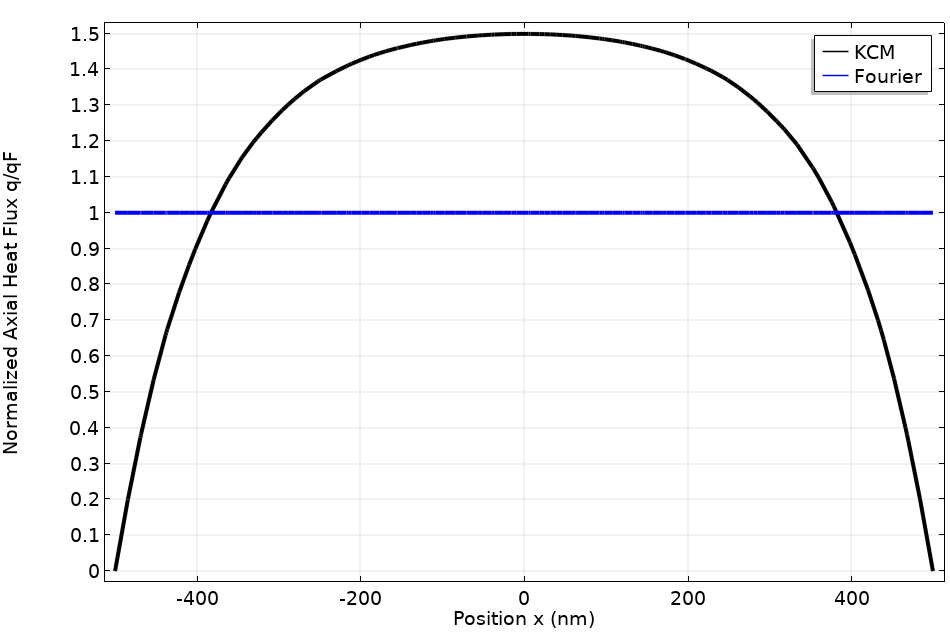
使用l = 100 nm 的 动能集合模型(黑色线条)和傅里叶定律(蓝线线条)得出的沿纳米线直径的热通量分布。
上图显示了2种不同情况下沿纳米线直径的热通量分布。黑色线条是使用非局部长度为 100 nm 的动能集合模型模拟的结果,蓝色线条是使用傅里叶定律预测的分布。由于这两个系统的平均通量相同,有效热导率也相同,因此得出的实验结果相同。
为了确定这个方程是否有效,需要进通过空间分辨测量来验证,这项工作目前已经通过一个热反射装置完成。
在 COMSOL Multiphysics® 中测量半导体衬底的热反射率
反射率 是一种材料属性,反映了物体表面反射电磁波的能力。该值与温度有关,这为热反射成像(TRI)测量提供了理论基础,在测量中利用表面反射的光来获取其温度。
美国普渡大学的比尔克纳米技术中心(BNC)最近开发了一种热反射装置,用于测量热量从顶部不同亚微米长度的金属线释放时,硅衬底的温度变化,结果如下所示。
![]()
使用动能集合模型模拟的由亚微米尺度金属线加热的硅衬底中的热通量(白色箭头)和温度梯度(黑色箭头)的方向。由于热通量与温度梯度矢量的方向不同,因此纳米线附近的热黏度非常重要。
比尔克纳米技术中心和巴塞罗那自治大学团队曾尝试是否可以用有效的傅里叶定律来描述这个实验,或者是否需要使用改进的模型。该装置几何结构的复杂性明显高于前一种情况,因此,需要寻找一种方法求解这种情况下的热特性。这可以通过将简单的动能集合模型理论方法与 COMSOL Multiphysics 中强大的 有限元求解器结合来实现。
在 COMSOL Multiphysics 中,我们能够完整地定义实验,包括衬底的一致性、氧化物绝缘层和顶部的金属线。与玻尔兹曼输运方程方法不同,这些简单的方程可以在完整的三维模型中轻松求解。
可以看出,傅里叶定律无法用热导率的标称值、拟合值或有效值来描述整组数据。
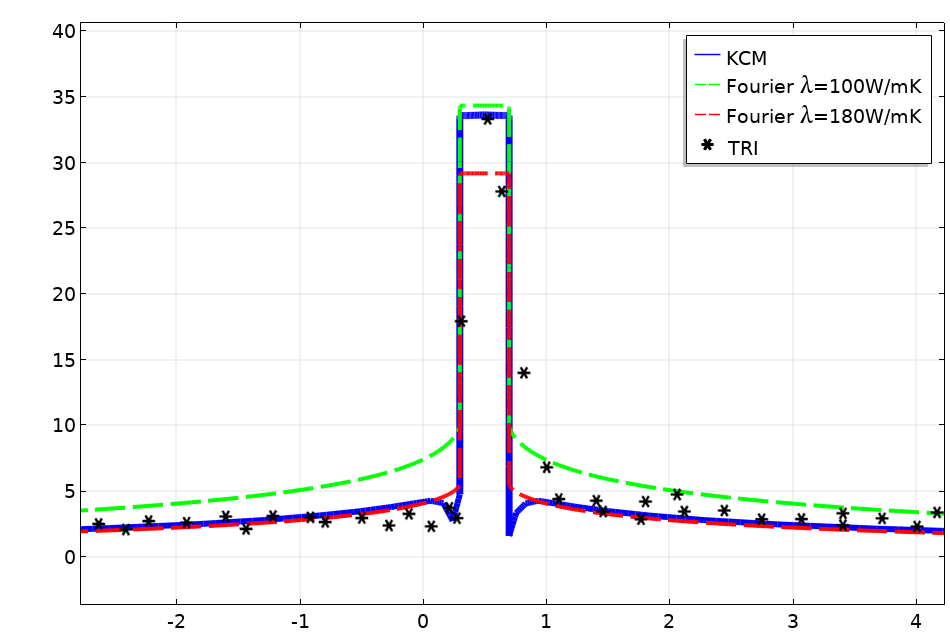
由热反射成像(TRI)测量的温度分布(星号)与热导率值增加的傅里叶定律预测的数据(红色线)的对比,热导率值降低的傅里叶定律(绿色线)拟合的加热器温度以及动能集合模型预测的数据(蓝色线)。
在上图中,红色线是使用傅里叶定律得到的结果,衬底的标称值为 λ。在这种情况下,我们观察到,加热器管线的温度被低估。如果使用傅里叶定律和 λ 的修正值来拟合加热器温度,如图中绿色线所示,尾部的值将被高估。
上述示例中无法预测全部数据,这清楚地表明傅里叶定律不是描述这些尺度下热输运的有效模型。
图中的蓝线显示了该几何结构的动能集合模型预测结果。可以看出,该模型能够利用热导率的标称值 λ=150W/mK 以及非局部长度 l = 180 nm 来预测温度计和尾部的温度分布。
结束语
本文介绍了如何使用像COMSOL Multiphysics这样的仿真技术来研究和理解输运过程的特性,如纳米尺度的传热等。预计未来几年,使用这种组合方法来模拟纳米尺度的传热将取得新的进展。
扩展阅读
了解更多关于这方面的主题,请阅读研究人员的完整论文:P.Torres、A.Ziabari、A.Torell、J.Bafaluy、J.Camacho、X.Cartoix、A.Shakouri,and F.X.Alvarez,“Emergence of hydrodynamic heat transport in semiconductors at the nanoscale”,Phys. Rev. Materials,2018 年 2 月,076001。
特邀博主简介
F.Xavier Alvarez是来自巴塞罗那自治大学物理系的一名副教授。他的研究课题为传输现象和非平衡态热力学。过去的几年,他一直致力于研究纳米尺度的热现象。这项研究的主要目标是获得更有效的输运方程,以提升电气工程行业使用的仿真技术的预测准确性。如今,他是巴塞罗那自治大学纳米输运研究团队的知识产权工程师。
文中使用的术语
- T:温度(SI 单位:K)
- q:热通量(SI 单位:W/m2/K)
- \lambda:热导率(SI 单位:W/m/K)
- l:流体动力学长度(SI 单位:m)



评论 (6)
ziqi chen
2022-04-19是否有KCM相关的MODEL可供下载学习
hao huang
2022-04-19 COMSOL 员工暂时还没有相关案例
Chao Huang
2023-01-18目前有KCM相关的案例可供下载吗
hao huang
2023-04-17 COMSOL 员工Huang Chao, 您好!
感谢您的评论。
目前官网暂时还没有相关案例
如果有进一步问题,建议您联系 COMSOL 的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
笑月 王
2025-03-26目前有KCM的相关MODEL可以学习吗,谢谢
Jun Leng
2025-04-07 COMSOL 员工感谢您的评论,目前官网还没有KCM相关案例。
如果有进一步问题,您可以联系 COMSOL 的技术支持团队:
在线支持中心:cn.comsol.com/support