
肥皂膜、悬链线电缆和光束有什么共同点?它们都有着使某些数量最小化的行为方式,这类问题普遍存在于生物学、经济学、弹性理论、材料科学和图像处理等科学和工程领域。我们可以使用 COMSOL Multiphysics® 软件中的内置物理场接口模拟很多这样的问题,在变分问题和约束系列博客中,我们将向您展示如何使用基于方程的建模功能解决变分问题。
函数的最小值
在初等微积分中,我们为单变量或多变量函数寻找最优值,即,寻找一个单一的数字或一组有限的数字 \mathbf{x} 使函数 f(\mathbf{x}) 最小(或最大)。在变分法中,我们寻找一个函数 u 使泛函 E[u(x)] 最小(或最大)。从某种意义上说,我们可以认为这是无限维优化。粗略地讲,就是泛函取一个函数并返回一个数值。例如,定积分就是一个泛函。
在工程问题中,这些泛函通常代表某种能量。例如,在弹性理论中,我们可以通过最小化总势能来找到平衡解。这个术语经常被用在其他变分问题上,例如变分图像处理。我们称泛函为“能量”——即使它在物理上不代表通常意义上的能量。
两个环之间的肥皂膜。
考虑 yz 平面上两个圆环之间的肥皂膜,其中心在 x 轴。我们希望找出这样一个函数 u_x,当我们绕 x 轴旋转它时,可以获得肥皂膜的形状。这个函数实际上是下面这个泛函的最小值,
(1)
更一般地说法是,在变分法中,我们正在寻找一个函数 u(x),使泛函的值最小,
(2)
大多数工程问题处理的是最多包含一阶导数的泛函。在本系列博客的开始,我们将在一个空间维度上关注这些问题。稍后,我们将推广到高维度、高阶导数和几个未知数。最后,由于最大值和最小值本质是一样的,因此我们将在后续文章中只讨论最小值。
除非另有说明,否则我们将处理的泛函是
(3)
求解变分问题
假设你发现自己被蒙住了眼睛进入一个山谷中,你怎么知道已经到达底部?(顺便说一句,摘掉眼罩不算)。你可能会用手和脚感觉周围的地面,如果你测试的每个区域都感觉都比你站的地方高,那么你就站在山谷的底部(至少是在一个局部的洼地)。在微积分和变分法中,同样的思想被用来检查最小值。在微积分中,我们测试相邻点,而在变分法中,我们测试相邻函数。
当且仅当对于微小值 \epsilon 以及每一个容许变分 \hat{u(x)} 都遵循以下表达式时
(4)
函数 u(x) 使得泛函 E[u(x)] 最小。
不是每个变分 \hat{u} 是可接受的,因为每一个 u+\epsilon \hat{u} 都必须满足解的约束条件。例如,对于两端固定在线上的肥皂膜,我们用于与最小函数进行比较的每个函数也必须固定在线上。因此,我们只考虑那些满足 \hat{u}(a) = \hat{u}(b) = 0. 的变分。我们将在后面的博客文章中详细讨论约束。
假设有足够的平滑度来进行微分,方程4 的必要条件是
(5)
在本系列中,我们不打算讨论移动或开放边界的问题。在这种情况下,我们可以把微分移到积分内部,并应用链式法则得到
(6)
请注意,我们只改变因变量 u 和它的导数,而不是空间坐标 x。
如果您对移动边界或界面的问题感兴趣,请查看博客文章:使用 COMSOL Multiphysics® 模拟自由液面的两种方法和在 COMSOL Multiphysics® 中用动网格为自由液面建模。
如 方程1 所示,对于肥皂膜,我们有 F(x,u,u^{\prime}) = u\sqrt{1+u^{\prime}2} \Rightarrow \frac{\partial F}{\partial u} = \sqrt{1+u{\prime}^2}, \frac{\partial F}{\partial u^{\prime}} = \frac{uu^{\prime}}{\sqrt{1+u’^2}}。因此,肥皂膜的变分问题是找到 u(x),以使
(7)
欧拉-拉格朗日方程
在经典变分法中,我们应用分部积分从变分 \hat{u} 中移动空间微分到解以获得欧拉-拉格朗日方程
(8)
并利用常微分方程(ODE)方法求其解。
在高维空间中,欧拉-拉格朗日方程变成了偏微分方程。
在我们的例子中,我们不需要使用欧拉-拉格朗日方程,所以不再进一步讨论它,原因是使用有限元方法来求解变分公式。例如,在 COMSOL Multiphysics 中,如果我们使用系数形式偏微分方程 或者一般形式偏微分方程 接口指定欧拉-拉格朗日方程,软件会在内部指定并求解相应的变分方程,既然如此,就没有必要再浪费精力吧?正如我们将在后面看到的,变分形式还提供了很自然地考虑求解域和边界条件的方式。
在 COMSOL Multiphysics® 中执行一个变分问题
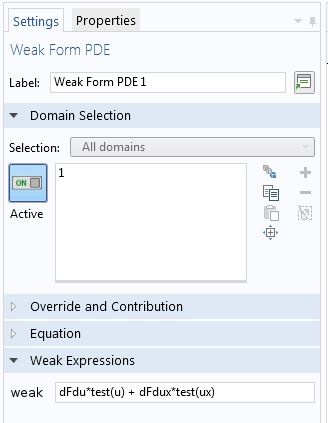
为了说明 COMSOL Multiphysics 中的变分问题,我们使用了弱形式偏微分方程 接口。那我们如何来对解 u 以及相应的试函数\hat{u} 求微分呢?对于后者,我们可以使用试函数算子。例如,对于肥皂膜问题,变分公式中的被积函数在弱形式偏微分方程 节点输入为 sqrt(1+ux^2)*test(u)+u*ux/sqrt(1+ux^2)*test(ux),如下所示。
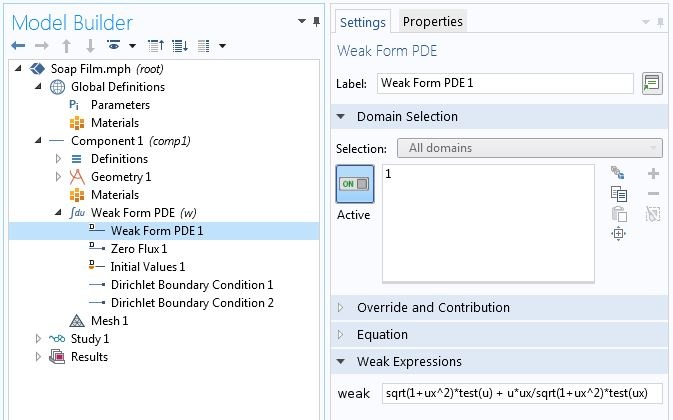
指定一个变分问题。
我们考虑一个简单的约束,即肥皂膜固定在左右两边的金属丝环上,左环和右环的半径分别是 1 和 0.9,因此我们知道主变量 u 在两端的值,可以使用狄利克雷边界条件 节点指定这样的边界条件。出于数值的原因,在这个特殊的问题中,我们提供了初始值 1 替代默认的初始值 0。
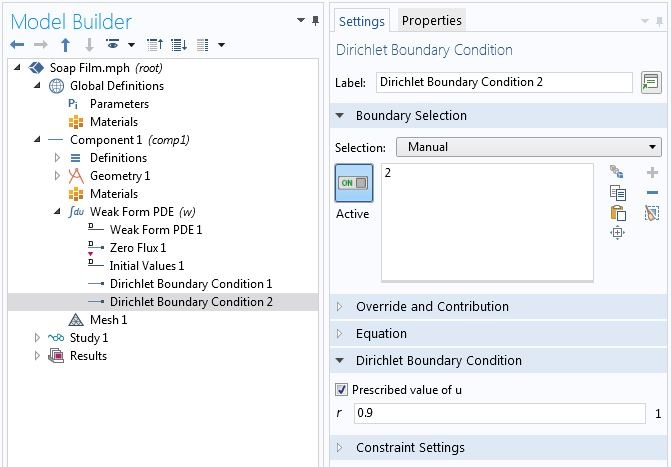
使用 狄利克雷边界条件节点指定已知的边界值。
如果我们求解,可得到下图所示的形状。
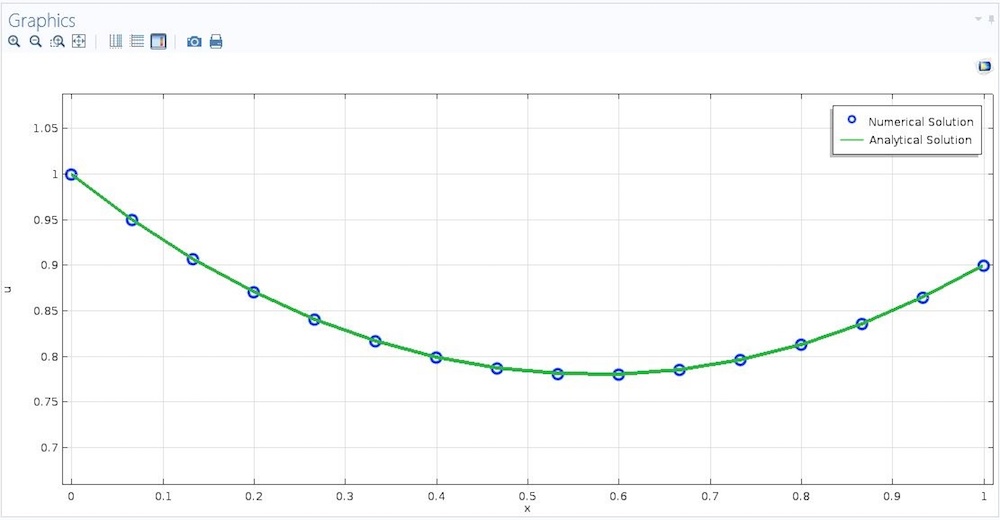
挂在两个垂直圆环之间的肥皂膜的轮廓。
指定一个更通用的符号形式
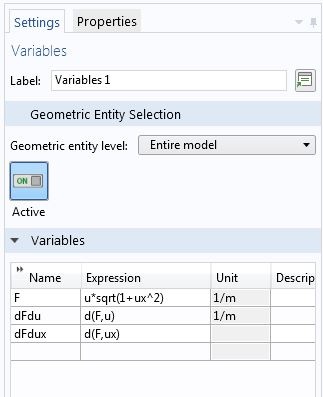
在上面的例子中,我们手动对 F 分别推导了 u 和 u^{\prime} 的偏微分,而利用 COMSOL Multiphysics 的符号数学能力,我们可以避免不必要的工作和潜在的错误。
用符号微分形式表达减少手动工作。
变分解与直接优化
我们还可以通过直接优化求解函数极小化问题。在这种方法中,我们不需要导出变分问题,但不利的一面是,它需要更多的计算工具。例如,在 COMSOL Multiphysics 中,直接优化需要优化模块。如果您对直接优化感兴趣,请查看我们的博客文章:如何求解两点间的最速降线。
后续操作
今天,我们向您展示了如何使用 COMSOL Multiphysics 软件中的弱形式偏微分方程 接口,您可以在弱形式概述这篇博文中了解更多关于弱形式的信息。
在接下来的文章中,我们将展示如何添加更复杂的约束,例如点约束、分布式约束和积分约束。本系列博客将逐步介绍更高的空间维度、更高阶的导数和更多物理场。敬请关注!
同时,您可以通过下面的按钮联系我们,了解更多关于 COMSOL Multiphysics 基于方程的建模特性。
查看变分问题和约束系列中的更多博客文章
- 第2部分:在变分问题中指定边界条件和约束
- 第3部分:强制约束中数值问题的处理方法
- 第4部分:实施不等式约束的方法
- 第5部分:图像去噪及其他多维变分问题



评论 (2)
金卫 林
2024-10-22很好的帖子,为什么容许变分到后面直接变成了试函数?是否可以这样理解:想要求解出一个u使得u对于任意一个符合条件的容许变分都在此处取极值,这种思想和试函数思想一致,两者之间可以相互转换
Jiliang Cai
2024-10-24 COMSOL 员工变分法推导得到的式(7)与有限元理论中的弱形式公式是一致的,所以可以直接使用有限元方法求解式(7)。关于有限元方法的更多介绍可以参考链接:https://cn.comsol.com/multiphysics/finite-element-method