
正如我们之前在“求解非线性稳态有限元问题”博客中所看到的,并不是所有的非线性问题都可通过阻尼 Newton-Raphson 法求解。尤其是当选择了一个不合适的初始条件或者设定一个无解的问题时,只会造成非线性求解器持续执行迭代而无法收敛。在此我们介绍一种更为可靠的非线性问题解决方案。
非线性问题示例
让我们再次考虑对弹簧施加应力的系统,弹簧具有非线性刚度:
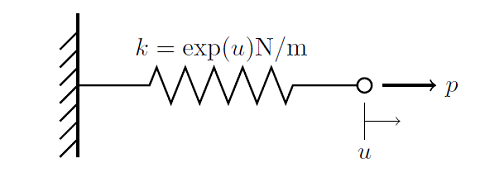
只要我们选择合适的初始条件(之前我们令 u_0=0),便可求解该问题。在“求解非线性稳态有限元问题”博客中,我们注意到在收敛半径外选择初始条件,譬如任 u_0\le-1 ,都会导致求解器失效。现在对于这个单一自由度的问题可以轻松地判断出它的收敛半径,但若是处理普遍的有限元问题时将会困难许多。所以不应试着求出收敛半径,而应首先对此类问题进行一些物理判断。
借助载荷递增改进鲁棒性
在此我们会向一个系统施加载荷,p_f ,设定初始条件 u_0,并尝试进行求解。如果我们施加载荷 p=0 会发生什么?牛顿第一定律表明,一个无载荷的系统将不会产生形变。所以若是施加一个无限小但是大于 0 的载荷 p_1又会怎样?可以合理地假设, Newton-Raphson 法会从初始条件 u_0=0 开始求解,最终将找到一个解 u_1。 同样也可以较为合理地认为,我们可以将载荷增加到 p_2 使得 p_1<p_2<p_f ,并再次得到一个解 u_2,只要载荷增量足够小即可。重复该算法,最后将达到最终载荷 p_f,以及期望的解。即从 0 载荷和 0 解开始,逐渐增大载荷直至达到期望的总载荷。下图展示了这个过程。粗箭头表示其中从特定的载荷值开始进行 Newton-Raphson 迭代。
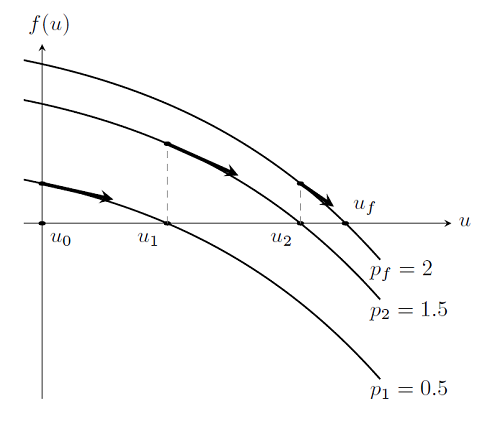
这个算法也被称作载荷的 延拓法。这种从接近 0 开始逐渐增加载荷的方法,提供了一种更为可靠的使用阻尼 Newton 法求解非线性问题的途径,因为之前一步的解对下一步而言是很好的初始猜测。
使用这个算法,我们不仅能更好地解决如何为 Newton-Raphson 迭代找到好的起始点的问题,还拥有了一种应对无解问题的算法。再次考虑弹簧拉伸后刚度减小的问题,即之前讨论过的 f(u)=2-\exp(-u)u,该问题无解。在本案例中,我们可以解析判定出,对于任意载荷 p>\exp(-1) 时都无解。但如果使用更小的载荷,那么系统会是稳定的。实际上在我们假设的场景中,系统处于双稳态;对于每一个载荷 p \le \exp(-1) 都存在双解,尽管我们只对从 p=0 和 u_0=0 开始产生的分支感兴趣。下面绘制出 f(u) 的图像:
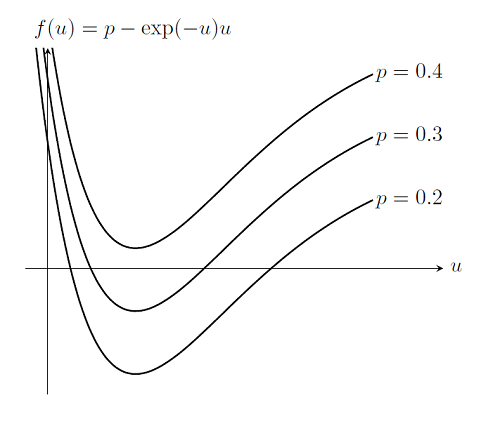
现在假设我们不知道载荷峰值在 p = \exp(-1) 处,并检验 COMSOL 求解 p = 0.2, 0.3, 0.4 时会发生什么。如果我们绘制出 p = 0.2, 0.3 时 f(u) 的图像,观察后发现 p = 0.4 时无解。 COMSOL 中的延拓求解器会自动在上一次成功的载荷值和下一次的期望载荷之间的区间执行一次搜索。即求解器会尝试进行回溯并找到一个可作为下一步起始值的中间解。当将 延拓法(或参数扫掠)用于在单一参数上求解稳态问题时,都会使用这个算法。那样的话,求解器将能够找到系统的最接近失效的载荷,这会是一项非常有价值的信息。
归纳和结论
我们已经介绍了载荷递增以及使用延拓法改善 Newton 法鲁棒性的概念。由于一个无载荷的系统存在已知解,而且我们已经看到该技术可以解决初始条件选值问题。此外,我们还了解到可以近似的求出破坏载荷。也因此,载荷递增是您在设定和求解非线性稳态有限元问题时应该理解的重要技术。
COMSOL 日志文件
让我们来看一下非线性有限元问题的日志文件。我们将设定并求解上文中描述的关于非线性弹簧在拉伸过程中刚度减小的问题。已知该问题无解,让我们来观察将发生什么:
求解器 1 中的稳态求解器 1 开始于 2013.07.15 11:26:46
参数化求解器
非线性求解器
求解的自由度数量:1
参数 P = 0.2
找到对称矩阵
相关变量的缩放:
稳态变量 u (mod1.ODE1): 1
迭代数 ErrEst 阻尼 步长 #Res #Jac #Sol
1 0.18 1.0000000 1 2 1 2
2 0.013 1.0000000 0.22 3 2 4
3 6.5e-005 1.0000000 0.015 4 3 6
参数 P = 0.3
迭代数 ErrEst 阻尼 步长 #Res #Jac #Sol
1 0.025 1.0000000 0.21 7 4 9
2 0.00069 1.0000000 0.031 8 5 11
参数 P = 0.4
迭代数 ErrEst 阻尼 步长 #Res #Jac #Sol
1 0.89 1.0000000 2.7 11 6 14
2 0.3 0.8614583 0.76 12 7 16
3 0.2 0.8154018 0.43 13 8 18
4 0.31 0.4194888 0.42 14 9 20
5 0.86 0.0836516 0.9 15 10 22
参数 P = 0.325
迭代数 ErrEst 阻尼 步长 #Res #Jac #Sol
1 0.089 1.0000000 0.4 18 12 26
2 0.014 1.0000000 0.13 19 13 28
3 0.0003 1.0000000 0.018 20 14 30
参数 P = 0.375
迭代数 ErrEst 阻尼 步长 #Res #Jac #Sol
1 0.099 1.0000000 0.32 23 15 33
2 0.079 0.9390806 0.19 24 16 35
3 0.2 0.3028345 0.24 25 17 37
4 0.94 0.0302834 0.95 26 18 39
... 部分日志文件省略 ...
参数 P = 0.368359
迭代数 ErrEst 阻尼 步长 #Res #Jac #Sol
1 0.046 1.0000000 0.057 80 49 112
2 0.061 0.3013806 0.072 81 50 114
求解器 1 中的稳态求解器 1 :求解时间: 0 s
物理内存:471 MB
虚拟内存: 569 MB
求解器同时报告了一项错误: 未能为所有函数找到一个解, 即使使用最大参数步长。 即使使用最小阻尼因子也不收敛, 返回解未收敛。
除了求解器报告现在调用了参数化求解器,日志文件的开头部分和以前一致。我们看到当 P = 0.2 和 P = 0.3 时,求解器完成求解。当 P = 0.4 时,求解器失效并自动追踪求出中间解。出于简洁的目的省略了一些中间步骤,但我们仍可以看到参数化求解器已十分接近峰值载荷的解析解。从该信息来看,我们可以使用一组新的参数重新求解并e更好地理解系统在接近破坏载荷时的行为表现,这些信息会非常有价值。



评论 (1)
林 振辉
2018-11-23以上介绍的是comsol求解器中自带的算法原理,还是可以通过用户调控实现的计算过程?(对于comsol 5.3a版本来说)