
在 2013 年的一份报告中,政府间气候变化专门委员会指出,地球的冰冻圈是“气候变化的自然整合者,提供了一些最明显的气候变化特征。”(参考文献 1)冰冻圈 是气候系统的一部分,包含冷冻水,占淡水的 80%。使用 COMSOL Multiphysics® 软件,我们可以模拟经典冰流动,分析冰冻圈动态,评估气候变化的影响,比如海平面上升。
高山冰川的寿命
1773 年,瑞士博物学家 André Bordier 首次用“流体”一词来描述高山冰川的运动。然而,科研人员花了一个多世纪才就冰川动态的统一描述达成一致。
冰川最令人困惑的一个方面是观察到冰表现出粘性和塑性,具体取决于冰川。英国物理学家 John Glen 利用应力和应变之间的非线性关系观察并描述了这种中间特性。这种经典特性称为剪切稀化,适用于许多不同的流体(如番茄酱和血液)。
任何高山冰川的寿命都可以示意性地描述如下:
- 雪堆积在气温较低的高海拔地区,并压缩成冰
- 冰在自重下开始变形并沿斜坡流下
- 冰在气温较高的低海拔地区融化
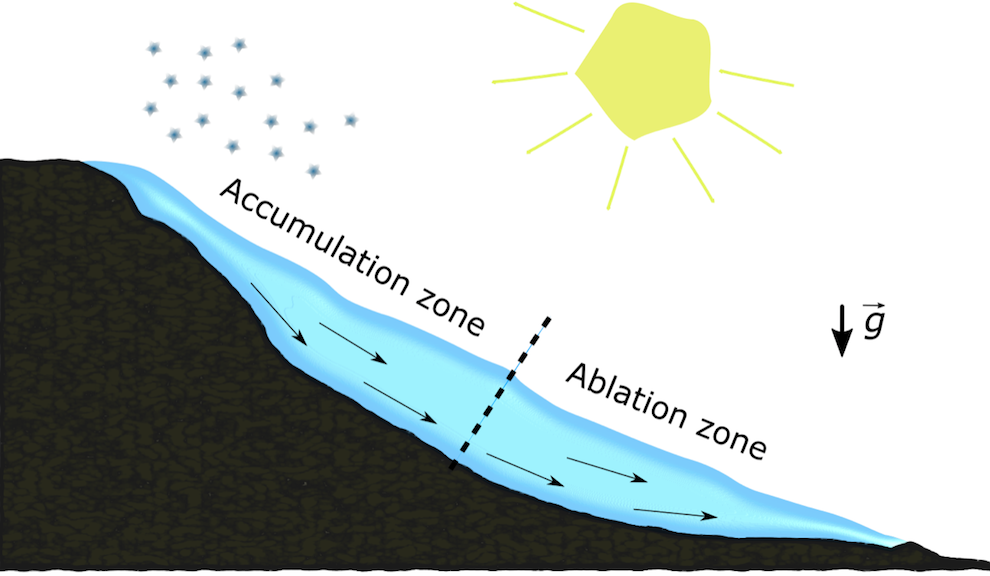
典型高山冰川的示意图。
因此,即使在稳定状态下(降雪刚好抵消了融化),冰也有一个动态过程:蠕变。这个流体模型是一个标准的纳维-斯托克斯方程,它有一个简化形式:斯托克斯(低雷诺数)近似,其中忽略了平流项。雷诺数的典型值是 Re = 10-15,因此这一假设无疑是成立的。
格伦流动定律
粘性流动的仿真通常假设应力和应变之间呈线性关系,这个假设描述了牛顿流体。实际上,许多流体在标准条件下是牛顿流体(例如,水和空气)。然而,许多流体在剪切时表现出粘度的变化。一种较为普遍的方法是使用本构定律来描述粘度 \mu随剪切速率的某个幂变化的情况。从数学上讲,\mu = \frac{1}{2}A^{-\frac{1}{n}}\dot{\gamma}^{n-1},其中\dot{\gamma}是剪切速率,经典定义为应变率张量 D(u)=\frac
{1}{2}\left(\nabla u + \nabla u^T\right)的模。
要完全定义流动定律,需要评估两个参数:
- 一致性, m=\frac{1} {2}A^{-1/n}
- 应力指数,n
对于冰,通常取 n=\frac{1} {3}。然而,冰的粘度不仅取决于剪切速率,还取决于温度和压力。于是我们定义一致性来表示这些依赖关系。定义冰模型一致性的经典方法是使用阿累尼乌斯定律(参考文献 1):A(T^
{\prime},p)=A_0e^{-Q/RT^{\prime}},其中 R 是理想气体常数,T’ 是相对于压力熔点的温度。
实际上,压力依赖性反映在冰的熔点随压力的变化上(随着压力的增加而降低)。利用克劳修斯-克拉佩龙关系,我们得到 T^{prime}=T+\beta p,其中 \beta=9.8\times 10^{-8} K Pa^{-1} 是克拉佩龙常数。A0 和 Q 的值目前存在争议。(参考文献 2)
粘性滑动
这种简明的流动定律是多年来通过严格的实验室工作凭经验得出的,它无法预测在现实冰川上观测到的高速度。人们花了很多年才明白原因到底在哪里。20 世纪 50 年代后期,J. Weertman 提出了基底滑动 的概念,并在业内形成共识。
在方程层面,基于分子相互作用的考虑,冰川的基底滑动定律与 H. Navier 一个世纪前提出的粘性滑动 概念没有什么不同。然而,对于冰流动而言,这个定律背后的物理过程仍然是一个争论性问题,并不是这篇文章的主题。我们回想一下,它写为 u_t=\frac{L_s} {\mu}\tau_{nt},其中 ut 是基底速度;\mu 是粘度(这里是非线性的);\tau_{nt} 是基底牵引力,或基岩的剪切应力;Ls 被称为滑移长度(参考文献 2 ),这个量在冰川流动建模中至关重要,这是因为它占下游质量通量的很大一部分,积少成多就产生流动运动,并且表现出类似于刚性运动的特性。
冰流动建模:现实示例
Mer de Glace,翻译为“冰海”,是一座高山冰川,位于夏蒙尼山谷上方法国阿尔卑斯山的勃朗峰地块。它被认为是法国最大的冰川,因其山谷冰川具有相当大的移动速度(每年约 100 米),而且在过去 80 年里它的体积显著减小,因此被广泛观察和监测。研究表明,该冰川平均每年损失 5 米厚,30 米长。
下图(右)是山谷冰川的几何图形,是使用 COMSOL Multiphysics 和 CAD 几何内核(可从 CAD 导入模块获得)建立的。几何图形大致模拟了冰海冰川(左)的测量和视觉效果。
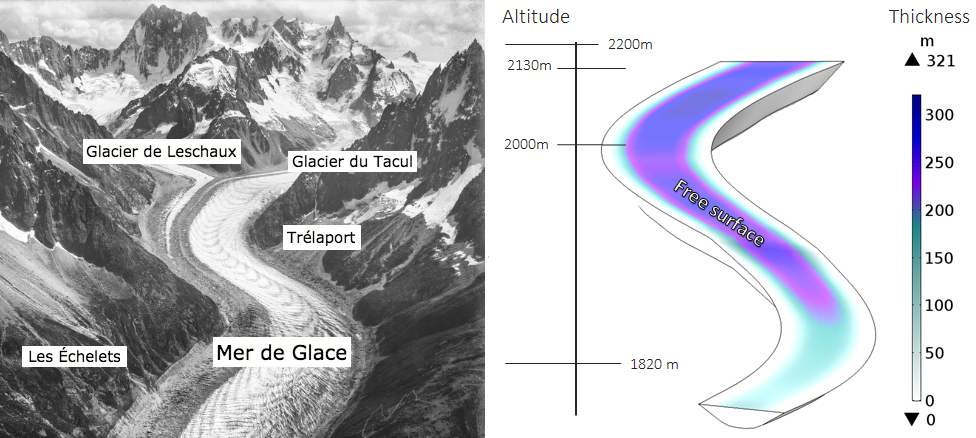
左:1909 年冰海冰川的航拍照片。图片来自公共领域,通过 Wikimedia Commons 分享。(作者添加的注释。)右:模型几何结构,按厚度着色。
我们来模拟冰块在自重和基底滑动作用下沿坡流下的非等温流动。
就流体而言,流入和流出边界条件是正常约束,对应于冰的外加压力,冰不包含在域中,它仅仅对应于指定的流体静压(或冰静压)。上游边界压在域上,因此有助于加快流向速度,而下游边界阻碍流动。冰川表面是自由表面。
就传热而言,表面被认为处于环境温度。与基岩接触的边界通常受到地热热通量的影响,地热热通量可以被模拟为边界条件。然而,由于这样的值在空间上是变化的并且通常是未知的,因此在本例中施加了温度。这样,我们确保冰保持在 0°C 以下,从而避免相变和潜热通量的贡献。值得注意的是,可以使用具有相变接口的材料 来分析这个方面。热量可以在流入边界和流出边界进入和离开域。
使用与几何结构的纵横比一致的拉伸网格。
外部天气条件是地球物理仿真的重要输入数据。通过“传热”接口直接访问 ASHRAE 2017 数据库,我们可以在全球超过 6000 个气象站输入一年中给定时间的平均外部温度和风速。这里,我们使用的数据来自瑞士阿尔卑斯山的圣伯纳德 站,该站距离冰海冰川 16 公里,位于 2 月 1 日中午的同一高度。环境温度施加在冰川表面,风速用于模拟表面的对流热通量。
仿真结果和讨论
首先,我们在没有基底滑动的情况下运行仿真,看看粘性流动对观测到的冰川速度有多大影响。预计结果是冰川顶部每年约 120 米,冰川末端每年约 90 米。
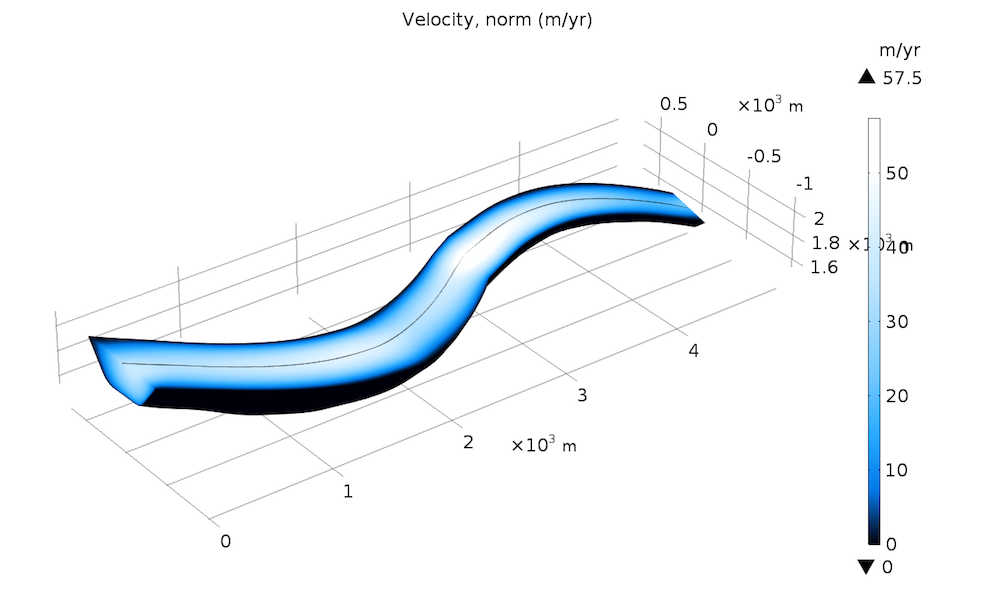
正如我们在图的左侧所看到的,仅仅根据此处描述的粘性定律,我们只能得到预期速度的 50%。
我们可以引入滑移长度 Ls = 250 m 的粘性滑移,然后再次运行仿真。下面,我们绘制了两种情况下沿着冰川中心流线表面的速度。
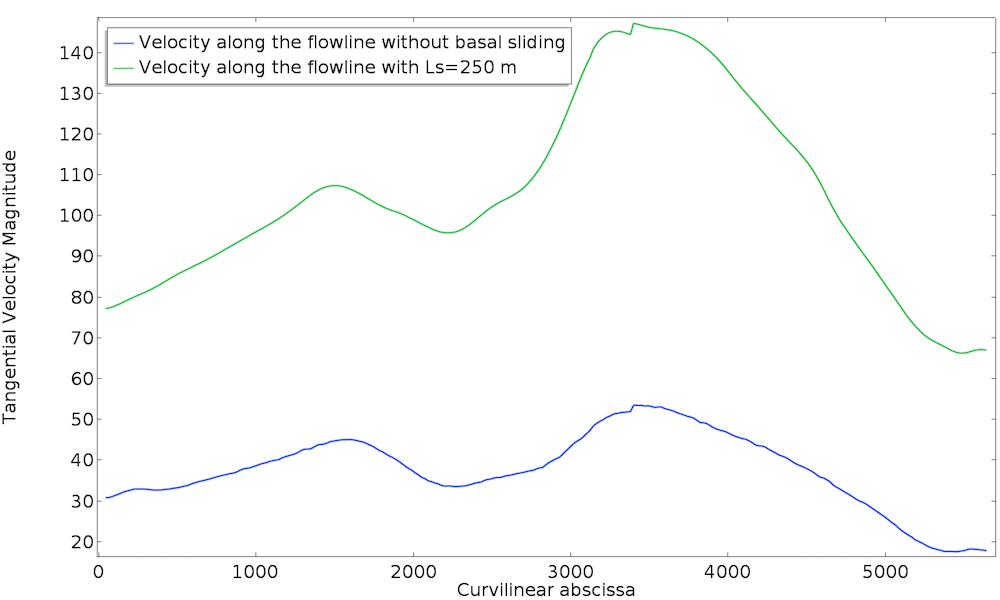
现在,全球范围内冰川消失速度要高得多,也更符合预期的幅度。值得注意的是,粘性滑动不仅引入了速度的纯粹变化。实际上,作为非线性粘度的函数,它增加了非线性贡献,因此它不是纯粹的刚性。对于滑移长度这个值,滑动贡献了表面速度的大约 60%。
接下来,我们继续讨论温度对冰流动的影响,这是近期气候变化研究中的重要耦合问题。为了量化全球变暖对冰川的影响,我们设想如下一个实验。数据显示,1940 年至 1970 年间,全球气温一直处于稳定状态,因此我们可以假设冰川在此期间达到稳定状态。测量结果表明,全球平均气温在 50 年间上升了约 1 度。因此,我们可以模拟这 50 年间平均气温稳定上升 1 度情况下冰的瞬态流动。
为了了解这种温度变化的影响,我们可以绘制表面和下游边界总质量流出量(单位为兆吨/年)的演变图。
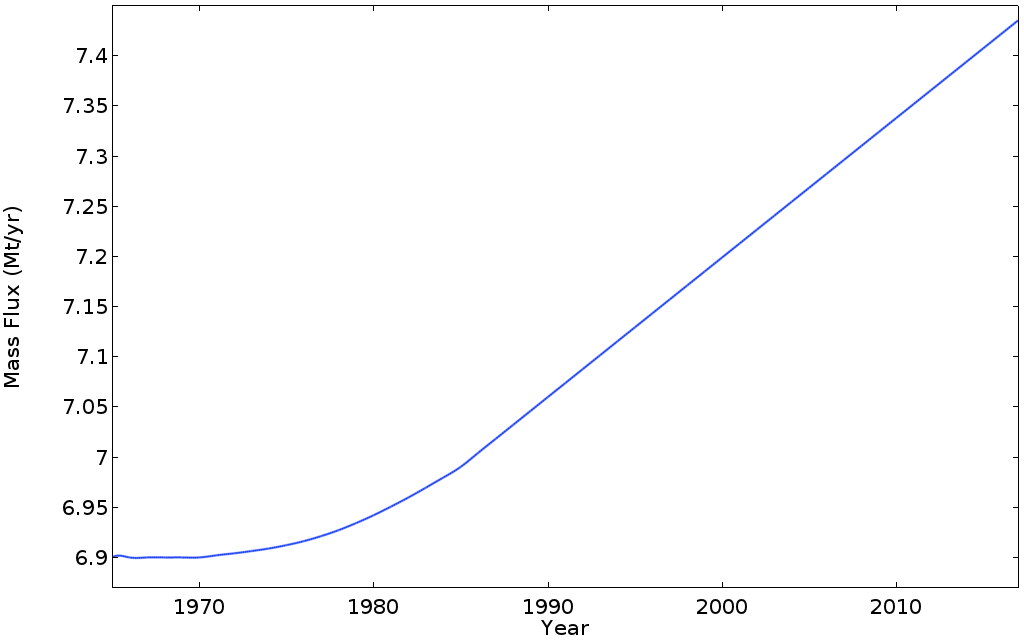
观察气温开始上升和冰川反应之间的延迟非常有趣。线性升温始于 1970 年,线性升温的质量通量始于 1985 年左右。在 1970 年至 1985 年间,质量损失的加速度缓慢增加,直至达到每年约 13 千吨的稳定值。这种延迟主要是由于地表温度变化传播到整个冰川的时间(从而增加了整个冰川的平均温度)。结果,输出质量通量在此期间增加了大约 10%,导致在此期间净增加了 15 兆吨的冰损失(与温度保持稳定的情况相比)。
我们将结果与之前讨论的冰海冰川数据进行比较。如果我们所在地区的冰川厚度每年减少 5 米(平均 5500 米长,600 米宽),我们每年将损失 15 兆吨的冰。即使假设所有这些冰通量都会在较低的海拔处融化(事实并非如此),2017 年计算的每年 750 万吨远小于过去几十年冰海冰川的实际质量损失。这是因为仿真没有考虑负表面质量平衡(积雪减去表面冰的融化)。
就建模而言,表面质量平衡是数据输入,本身就是复杂物理学的产物。例如,较热的夏季对冰川有很大的影响,这是因为通常夏季降落的少量雪可以起到防御太阳辐射的作用,从而保护冰川在夏季不会大量融化。如果夏季没有降雪,那么冰川融化量会大得多。这种额外的融化导致液体水通过裂缝大量渗透,最终形成冰下水文网络,主要通过冰-基岩界面的润滑和水压“抬升”冰川,在基底滑动中发挥重要作用。
由于几何形状会影响动力学,因此我们针对冰川的给定几何形状执行仿真,忽略了几何形状因表面质量平衡和动力学而发生的演变,这也是很重要的一个方面。
关于冰流动建模的总结性思考
本篇博客文章介绍了如何用 COMSOL Multiphysics 建立和求解一个简单的冰川流动模型。COMSOL® 软件为此类建模中涉及的大多数问题提供了专用功能。本例和一般冰川学的主要局限是数据;通常包括地形数据、基底滑动长度、表面质量平衡、堆积和融化。
在接下来的博客文章中,我们将演示如何通过“优化模块”使用灵敏度分析和数据同化来充分利用冰川仿真。敬请关注!
后续操作
参考文献
- Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, T.F. Stocker et al. (eds.), Cambridge University Press, 2013.
- R. Greve and H. Blatter, “Dynamics of Ice Sheets and Glaciers,” Springer, 2009.



评论 (3)
广 李
2023-03-13请问贵单位可以分享一下这个模型吗?
hao huang
2023-03-15 COMSOL 员工您好,本篇博客作者暂未提供相关案例,您可以在“案例下载”页面中搜索不同关键词查看相关内容:http://cn.comsol.com/models
海波 赵
2024-02-21这里面应该有冰的融化,冰和水的流动,冰的粘度是如何处理的呢