
褶皱研究是一个跨学科的课题,无论是空间工程领域的充气天线,还是生物工程中常见的皮肤褶皱研究均有所涉及。无论从事哪个领域工作的工程师和研究人员,只要涉及薄结构,都熟悉褶皱产生的基本原理:当薄结构受到压应力时,刚度不足或刚度降低将会产生褶皱。这篇博客,我们将探讨如何使用 COMSOL Multiphysics® 软件模拟褶皱。
引言
在结构仿真中,薄结构通常使用壳单元或膜单元模拟。壳单元会考虑结构的弯曲刚度,而膜单元不会。这一基本差异决定了这两种单元类型处理褶皱仿真的方式。当考虑弯曲刚度时,与壳模拟一样,在以弯曲刚度为特征的临界压应力下,会出现褶皱。另一方面,如果不考虑弯曲刚度,与膜模拟一样,则在一开始产生压应力时就会出现褶皱。
在这两种情况下,褶皱都被认为是一种不稳定特征,也称为 局部屈曲。使用壳单元模拟褶皱时,有必要进行屈曲后分析。值得注意的是,网格离散化和任何几何缺陷都会对最终结果产生重大影响。壳模拟的优势在于可以获得有关波长和振幅等褶皱特征的详细信息。然而,在许多仿真场景中,皱褶的详细特征并不特别重要;相反,主要目标是避免问题区域出现皱褶。在这种情况下,使用膜单元模拟褶皱可能更有优势,因为这种方法计算成本低,而且数值稳定性更好。
接下来,我们将逐一介绍这两种模拟方法。在 COMSOL Multiphysics® 中,壳单元和膜单元分别使用 壳 接口和 膜 接口模拟。

另一个熟悉的褶皱示例:船帆。照片来自Unsplash,由 Karla Car 提供。原作品经过修改。
使用膜接口仿真
使用 COMSOL 中的 膜 接口模拟变形的薄结构存在以下三种可能的状态之一:
- 绷紧的 — 当两个面内主应力均为正值时
- 松弛的 — 当两个面内主应力均为负值时
- 褶皱的 — 当面内主应力之一为负值时
常规膜理论采用的是考虑了褶皱区域中压应力的全应变能公式,从而产生了不稳定的解。为了避免由压应力产生的平衡不稳定性,我们提出了(基于张力场理论的)修正膜理论。修正膜理论在褶皱区域返回单轴应力状态,在松弛区域返回零应力状态,从而避免了平衡不稳定性。修正膜理论有两种主要方法: 修正的变形张量和修正的本构关系。
修正的变形张量公式
为了理解褶皱动力学,我们来看下面这幅图:
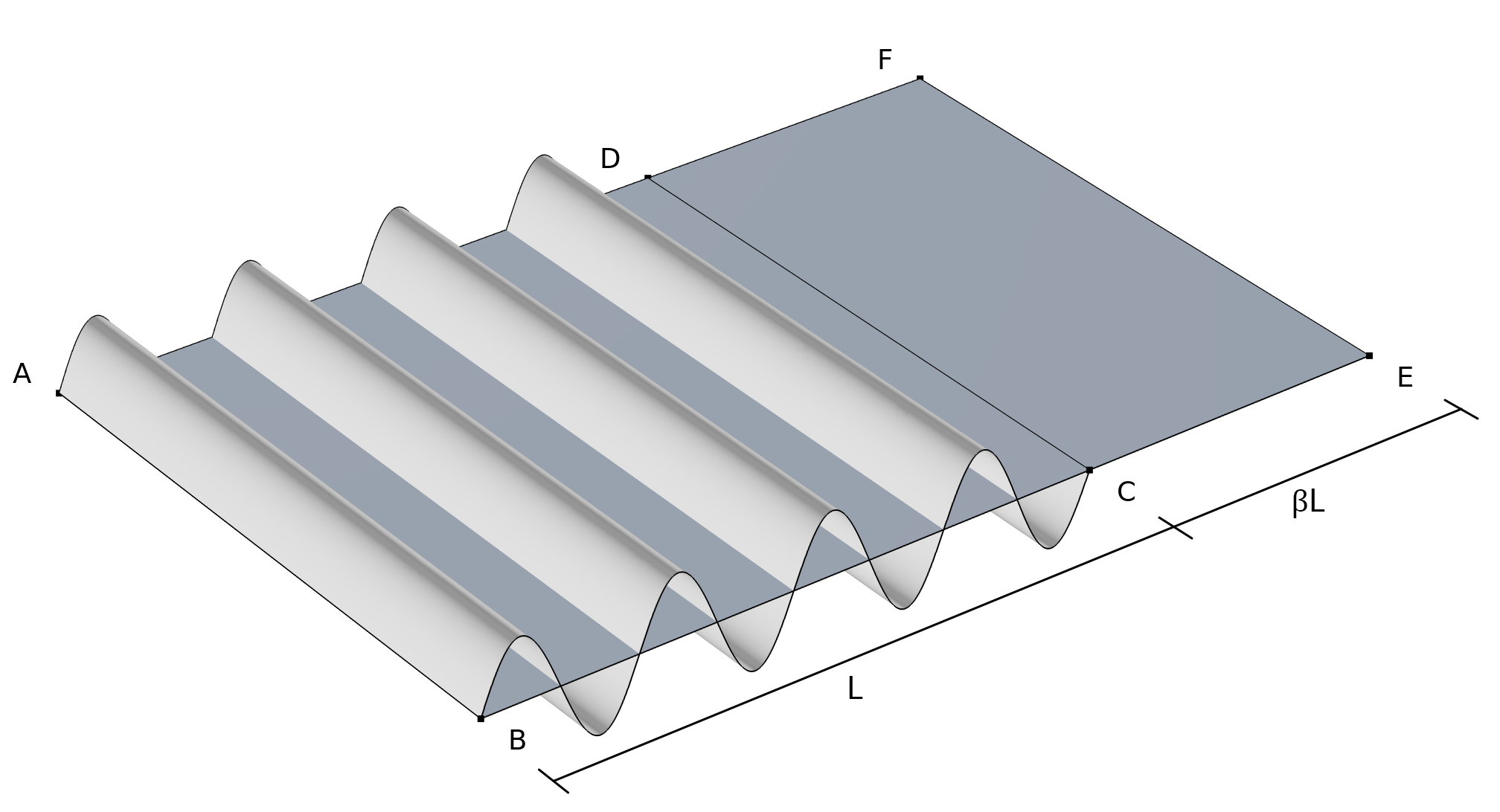
褶皱动力学。弧形表面 ABCD 代表褶皱构型,平面 ABCD 代表平均构型,平面 ABEF 代表加长构型。
对于褶皱膜,上图显示了三种不同的动力学描述:
- 变形张量 \widetilde{\bf{F}} 将参考构型映射为真正的皱褶构型(弧形表面 ABCD)。
- 不适合测定褶皱膜中的应变场
- 变形张量 \bar{\bf{F}} 将参考构型映射为平均构型(平面 ABCD), 其面积小于实际皱褶面积。
- 不适合测定褶皱膜中的应变场
- 变形张量 \bar{\bf{F}} 将参考构型映射到一个虚构的加长构型(平面 ABEF),其面积等于实际皱褶面积。
- 适用于测定褶皱膜中的应变场
假设褶皱发生在 \bf{n}_2 方向,且 \bf{n}_1 为单轴拉伸方向, \bar{\bf{F}} 为修正的变形张量,记为
式中, \beta是拉伸/褶皱参数 (参考文献1)。符号 \otimes 表示两个向量的外(二元)积,产生一个张量。\beta=0 表示绷紧条件。根据正交条件和张力场理论,
其中, \bf{\sigma} 是柯西应力。用第二皮奥拉-基尔霍夫应力表示为
假设平均构型已知 (\bf{F}), 那么未知数就是 \bf{n}_2 和 \beta。
让我们把这些方程映射到更方便的参考构型中,因为膜动力学和材料特征都在参考构型中。假设 \bf{h} 是参考构型中与矢量 \bf{n}_2 相对应的矢量。因此,虚构的格林-拉格朗日应变张量 \bar{\bf{E}} 可写成
式中,\bf{C} 是平均右柯西张量, \bf{N}_2 是参考配置中的单位向量, \beta^* 是新的皱褶参数。
膜表面有一个坐标系,有两个面内正交单位矢量, \bf{e}_1 和 \bf{e}_2。 \bf{N}_1 和 \bf{N}_2 与角度 \alpha 的关系式为
下列非线性耦合方程用于求解两个未知数 \alpha 和 \beta^*,
这两个非线性代数方程可以用牛顿-拉夫森方法求解:
f_{1,\alpha} & f_{1,\beta^*}\\
f_{2,\alpha} & f_{2,\beta^*}
\end{pmatrix} \begin{pmatrix}
\Delta \alpha\\
\Delta \beta^*
\end{pmatrix} = \begin{pmatrix}
-f_1\\
-f_2
\end{pmatrix}
式中, \alpha 和 \beta^* 在每个高斯点上应用局部牛顿-拉夫森方法,并在全局范围内进行迭代求解得到的。
褶皱功能
修正的变形张量方法可以通过 皱褶 子节点实现,该节点内置在 膜 接口的 线弹性材料 和 超弹性材料 节点下。皱褶 子节点有三种不同的局部牛顿-拉夫森方法的终止准则选项,并允许用户调整公差。
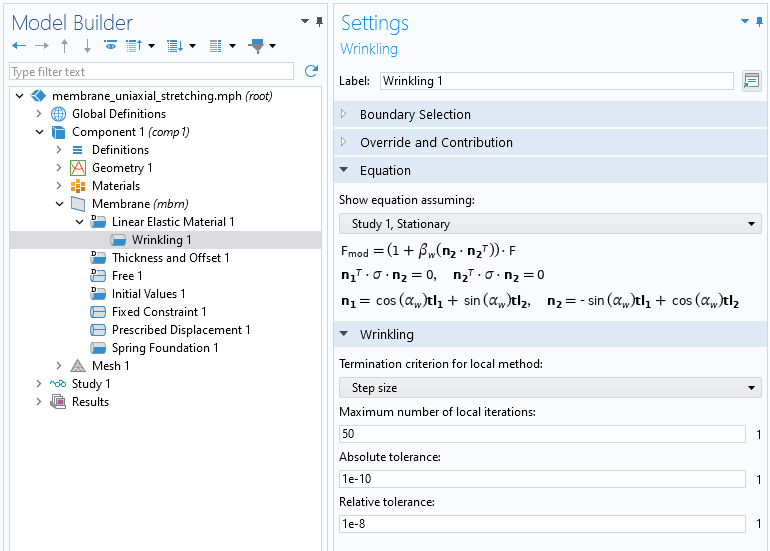
线弹性材料 特征下的 皱褶 子节点。
COMSOL 案例库中有几个示例展示了如何使用 膜 接口的内置功能建立褶皱模型。矩形膜的单轴拉伸 模型是一个容易分析验证的简单模型。在这个例子中,将数值结果与分析结果进行了比较,如下图所示:
矩形膜的皱褶区域用暗红色显示。 左图使用的是各向同性材料,右图使用的是各向异性材料。这两幅图比较了分析结果与计算(数值)结果。
方形安全气囊的膨胀模型更符合实际情况,因此也更加复杂。该模型展示了使用线弹性材料的方形安全气囊在充气过程中的起皱情况。类似的,方形超弹性气囊的膨胀, 模型使用的是超弹性材料。
使用线弹性材料模拟的方形安全气囊。褶皱区域用暗红色显示。
另一个使用 膜 接口内置功能分析褶皱的示例是圆形膜的扭转模型。在该模型中,仅在圆形膜的内边施加了扭矩以产生褶皱。在这个示例中,可以观察到不同网格模式和离散度对褶皱模式的影响。
修正的本构关系
如上所述,COMSOL Multiphysics® 中的 褶皱 子节点使用的是修正变形张量公式。由于软件的灵活性,也可以使用第二种方法模拟褶皱:修正的本构关系。
第二个公式对皱褶区域的本构关系进行了修改。用于皱褶区域的应变能称为 松弛应变能,而用于绷紧区域的应变能也被称为 完全应变能。这种方法适用于所有各向同性超弹性材料模型,但为了简单起见,这里考虑的是 neo-Hookean 不可压缩材料。用主拉伸 \lambda_1 和 \lambda_2 表示的全应变能密度可写成
主柯西应力 \sigma 的计算公式为
各方向的柯西主应力分别为
假设拉伸发生在第一主方向,褶皱发生在第二主方向。那么,在褶皱区域,以下等式必须成立:
该方程确定了褶皱区域的单轴应力状态,褶皱方向的应力变为零。根据褶皱方向上的零应力,可以得到主拉伸的褶皱条件:
因此,皱褶区域由以下不等式确定:\lambda_2 \sqrt{\lambda_1} < 1 。在全应变能中插入根据主拉伸得到的褶皱条件,neo-Hookean松弛应变能的计算公式为
松弛应变能与褶皱方向的拉伸无关,这意味着该方向的柯西应力将自动变为零。
利用上述褶皱条件和能量密度,绷紧区域和褶皱区域的应变能密度可写成
可以证明,对于各向同性膜,修正的变形张量和修正的本构关系公式是等价的(详见参考文献1 )。然而,修正的本构关系法只适用于各向同性膜,而修正的变形张量方法更为普遍,也适用于各向异性膜。
比较 COMSOL Multiphysics® 中的计算公式
在不同厚度圆筒膜的起皱案例模型中,我们对两种公式进行了比较,发现结果是一致的。在该模型中,圆柱形膜首先被轴向拉伸,然后用水压进行充气。在充气过程中,外边界固定。
在 COMSOL Multiphysics® 中,可以通过选择 超弹性材料 特征的 用户自定义 选项来实现修正后的本构关系。请注意,此案例模型中 neo-Hookean 材料的应变能是专为不可压缩的各向同性膜编写的。在这个示例中,不应该使用内置的不可压缩公式,因为它增加了可能导致冲突的额外项。您可以在用户定义的超弹性材料中使用 可压缩 选项,该选项完全按照所编写的内容使用给定的应变能密度。
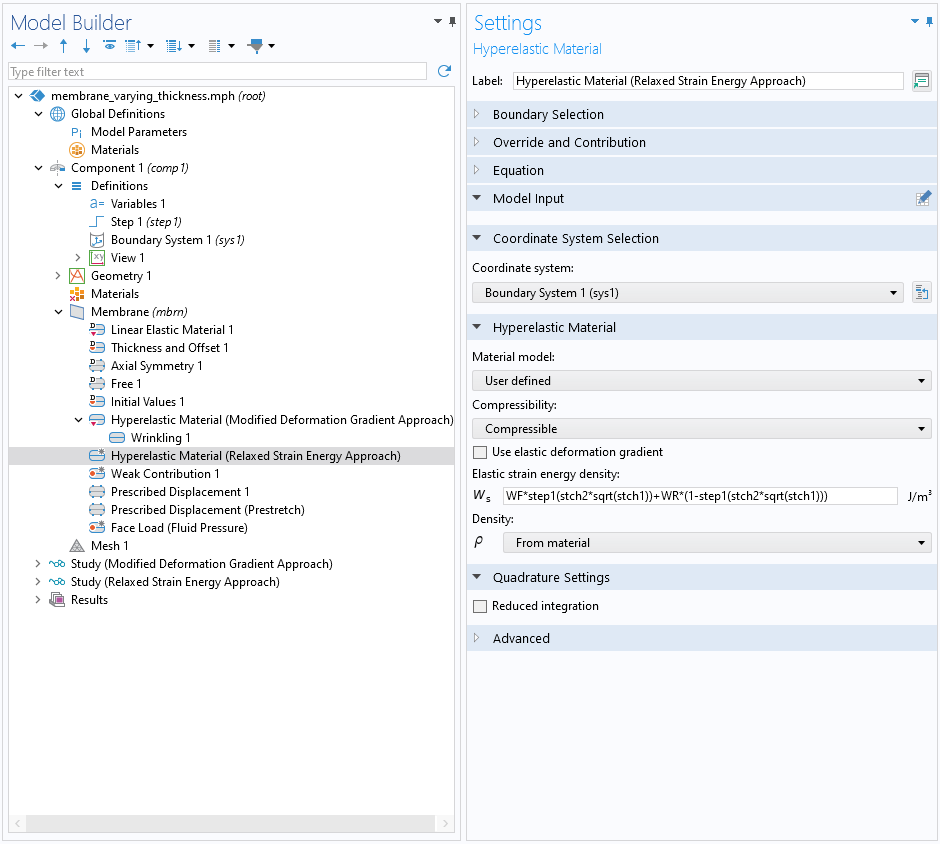
皱褶 子节点(使用修正后的变形张量公式)和用户定义的超弹性材料模型(使用修正后的本构关系公式)。
下图展示了采用两种方法模拟的不同水位高度下圆柱形膜出现的褶皱区域。结果表明,两种方法基本是等效的,并且得出的结果也相同。
圆柱形薄膜的皱褶区域用深红色显示。左图使用的是修正的变形张量方法,右图使用的是修正的本构关系方法。注释显示了膜中不同的流体高度,膜高 80 mm,半径为 10 mm。
使用壳接口仿真
使用 壳 接口时,褶皱的处理方法基于分岔分析。由于压应力的作用,褶皱被认为是一种局部屈曲现象,因此需要进行后屈曲分析来模拟褶皱。使用后屈曲分析的优势是可以确定褶皱的波长和振幅。处理褶皱的第一步是进行预应力特征值分析,以确定潜在的屈曲模式。然后,选择几个具有适当比例的屈曲模式,并将其作为后屈曲分析的几何缺陷。
在 矩形片材的单轴拉伸模型中,通过使用壳的后屈曲分析来研究矩形薄板中褶皱的产生。下图显示了包含该分析所需节点的模型树。
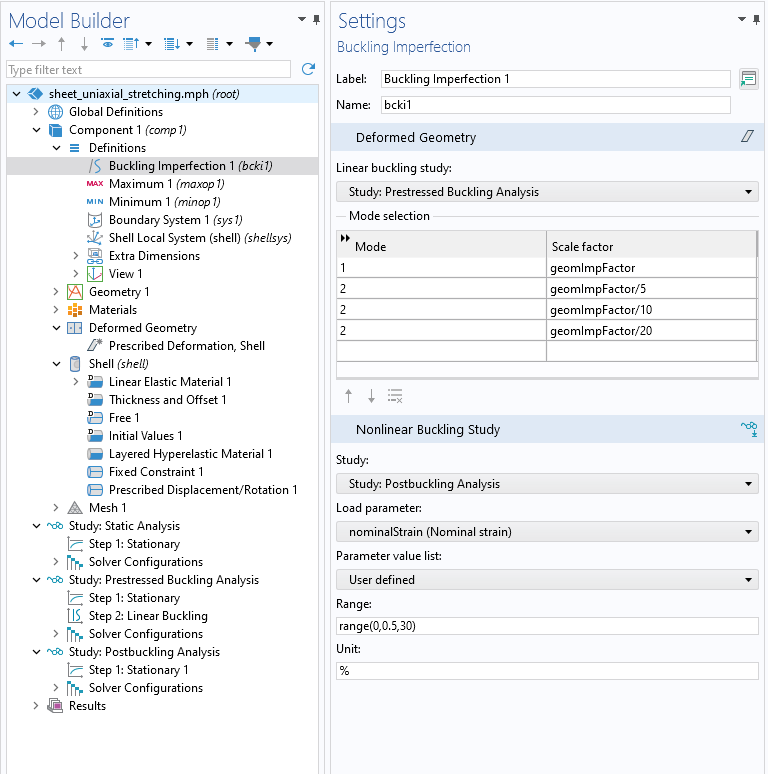
矩形片材的单轴拉伸模型的 屈曲缺陷节点和所需的研究
该教程模型的第一步是通过静态分析确定潜在的褶皱区域。在此阶段,矩形板受到单轴拉伸。目标是找到第二主应力变为压缩应力的区域。随后,使用 稳态 和 线性屈曲 研究步骤进行预应力屈曲分析。
对于后屈曲分析,可以使用 屈曲缺陷 节点,如上图所示。在该节点中,可以选择所需的屈曲模式数量及其相应的缩放因子。然后将这些缩放模式组合起来,作为几何缺陷应用于后屈曲分析。通过 屈曲缺陷 节点,还可以创建参数非线性屈曲研究。
下面的动画显示了矩形片材在单轴应变增加时产生的褶皱,第二幅图则显示了沿褶皱方向中心线的褶皱幅度。起初,当矩形片材上的应变增加时,褶皱开始出现。褶皱幅度随着应变的增加而增大,直到达到临界值,之后开始减小。在达到某个应变值时,褶皱幅度变得非常小。
屈曲后分析中的褶皱。颜色方案显示了 褶皱振幅,其中蓝色代表负值范围,红色代表正值范围,绿色代表零位移。
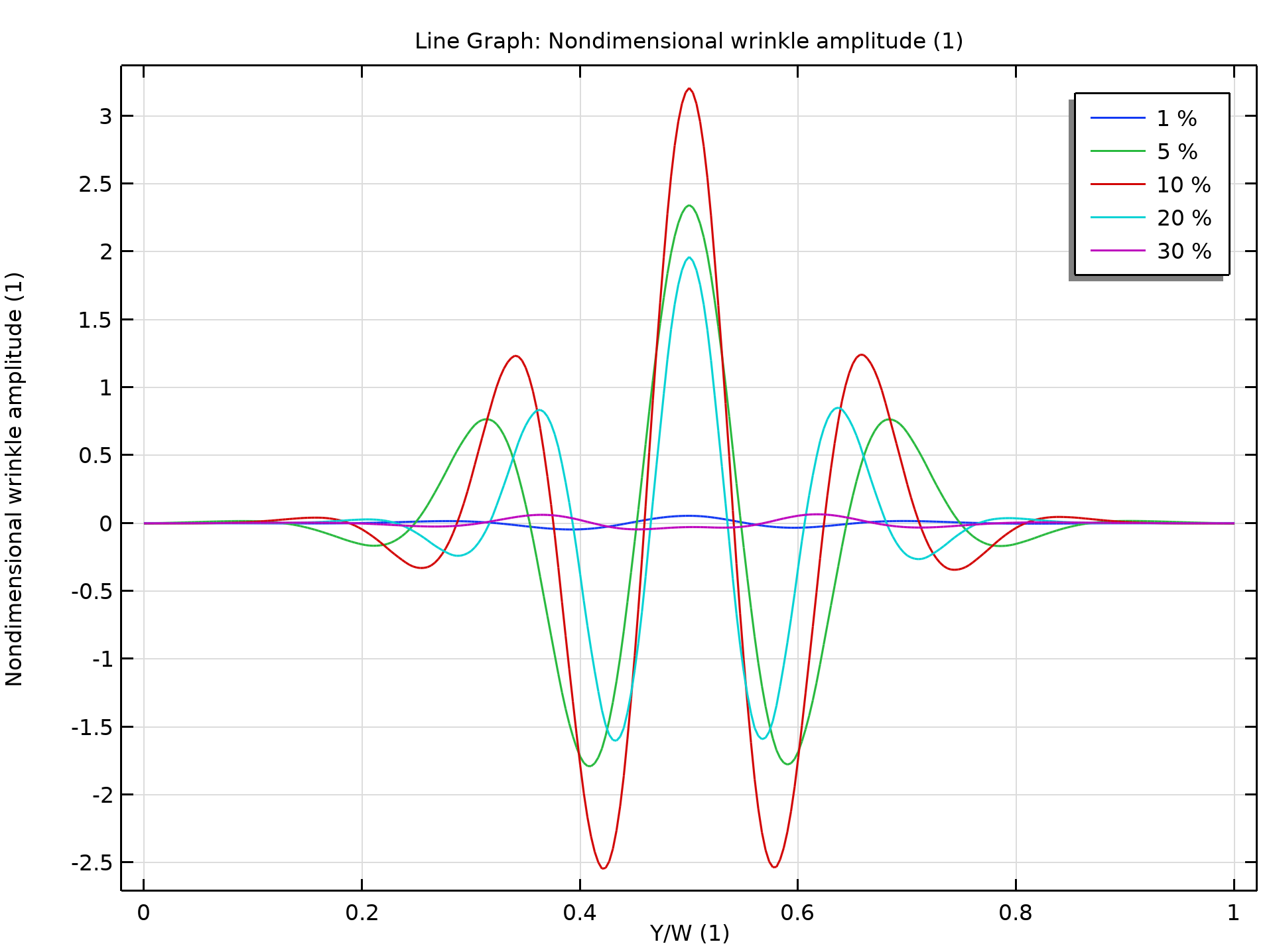
后屈曲分析中的皱褶振幅。
结语
如文中所演示的,您可以在 COMSOL Multiphysics® 中使用 膜 和 壳 接口模拟皱褶。可以通过修正变形张量或本构关系对皱褶进行膜分析。这种方法快速且计算效率高,能准确识别皱褶区域和应力分布。但是,它无法提供有关皱褶振幅和波长的信息。另一方面,皱褶的壳分析不仅耗时长,计算量大,还对几何缺陷输入敏感,但它能准确预测应力分布和皱褶区域,并能提供有关皱褶振幅和波长的宝贵数据。这两种分析类型各有优缺点,工程师可根据具体的建模要求选择其中一种分析类型。
参考文献
- A. Patil, Inflation and Instabilities of Hyperelastic Membranes, PhD thesis, Royal Institute of Technology (KTH), Stockholm, 2016.
- H. Schoop et al., “Wrinkling of nonlinear membranes,” Computational Mechanics, vol. 29, pp. 68–74, 2002; https://doi.org/10.1007/s00466-002-0326-y






评论 (0)