
在石油和燃气行业,如何进行安全且经济的钻井是一个重大问题。除了常规的探井风险,油井本身也具有无法预知和不可避免的未知风险。本篇博文主要介绍如何通过数值仿真来避免这些未知风险,目的是通过对多分支井的稳定性进行分析,确定该油井是否需要采用昂贵的机械加固。
多分支井钻井
随着钻井技术的发展,上个世纪出现了在一个油井上分出多个不同分支井的多分支井钻井技术。不管是在油气还是地热生产中,该方法都可以提供更大面积的储库。
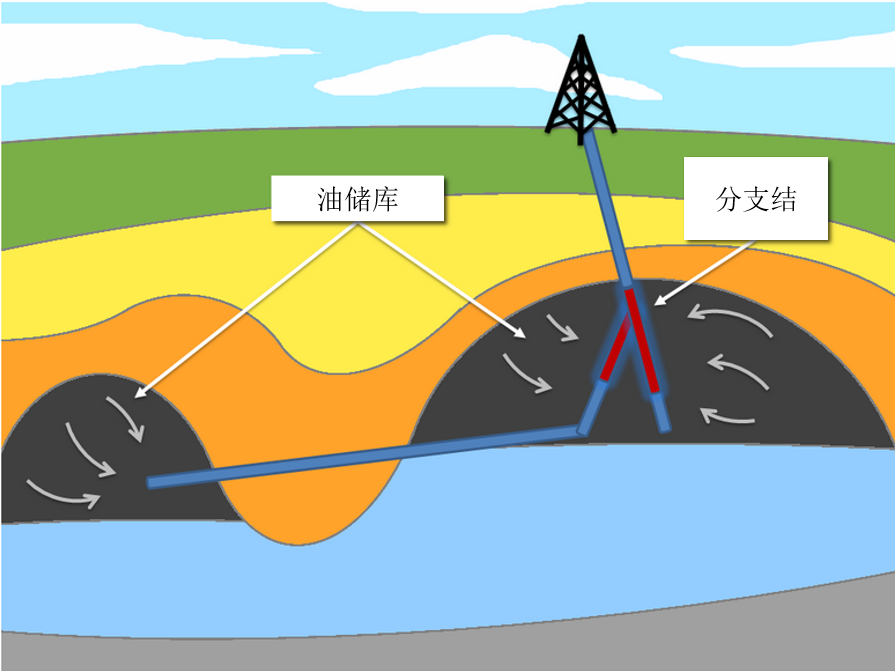
Natural resource recovery:机械泵将石油从储油库运送到地表,邻近的储油库通过与分支结相连的分支井进行开采。
通常分支结的稳定性远不如单油井,需要采用套管或者内衬进行加固。钻井工作完成后,整个油井将是开放的。当开始开采工作时,抽油作业会使油井承受更多的应力。油井套管非常昂贵,会极大的增加开采成本,因此,需要尽量避免采用额外的加固措施。
问题是:在不采用油井套管的情况下,开放的油井是否能够稳定?
多分支井仿真
油井链的最薄弱环节决定整个油井链的强度。因此仅需对多分支井最薄弱的分支结进行仿真,就可以判定整个多分支井的稳定性。如果分支结稳定,那么整个多分支井将保持稳定。假定多分支井只会发生弹性形变,就可以采用 COMSOL 的地下水流模块和固体力学接口进行仿真。
其中不必对油井内部的流体进行细节仿真,而是通过井壁压强来直接等效油井内部的流体作用;而井壁压强与抽油泵工作状态以及分支结的深度有关。
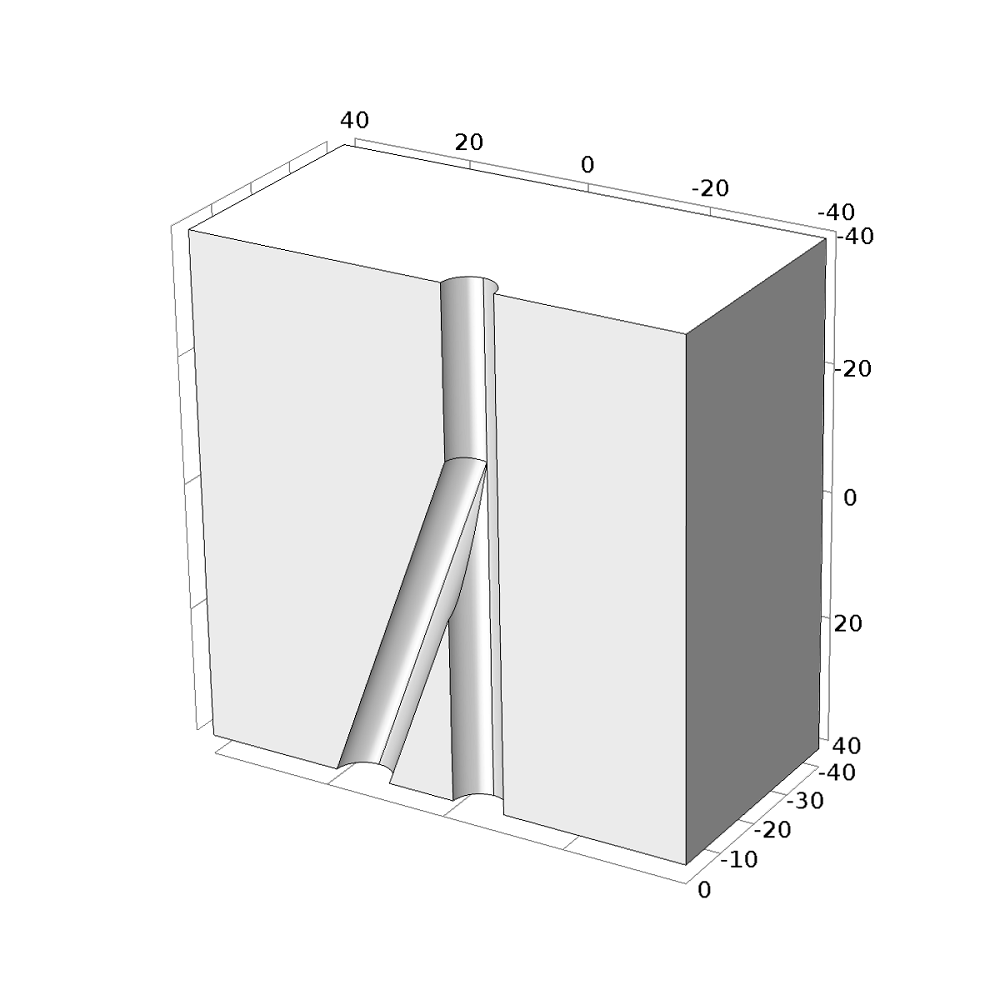
利用分支结的对称性,可以仅对分支结的一半进行仿真,从而大幅降低模型的规模,节约计算资源和时间。
物理方程
多孔介质中的地下水流采用达西定律和连续性方程进行描述:
其中, \kappa 为渗透系数,\mu 为动力粘滞系数, p_f 为石油的孔隙压力。开采作业进行过程中,通过油泵使得石油在空隙中流动,会导致井壁压强和孔隙压强下降。
柯西应力 \sigma 和孔隙压力 p_f 有如下关系,导致井壁压强载荷影响形变:
其中,弹性矩阵 \boldsymbol{C}=\boldsymbol{C}(E,\nu),其中 E 为杨氏模量,\nu 为泊松比;\epsilon 为应变张量,\alpha_B 为 Biot-Willis 系数。流体和准静态形变之间有如下关系:
其中 \boldsymbol{F} 表示所有的外部体力。
边界条件和模型参数
油井是石油的唯一出口,因此垂直油井轴向的边界都可采用 无流动边界条件。前文提到利用油井的对称性可对分支结的一半进行模拟,因此在流体和结构接口中对称面均采用对称边界条件。由于油井是可以自由变形的,因此所有的外部边界都采用约束运动边界。模型采用的参数如下表所示。
| 变量 | 描述 |
值 |
|---|---|---|
| \rho_f | 流体密度 |
0.0361 lb/in3 |
| \rho_s | 固体密度 |
0.0861 lb/in3 |
| \mu | 流体动态粘度 |
1·10-7 psi·s |
| \kappa | 渗透率 |
1·10-13 in2 |
| E | 杨氏模量 |
0.43·106 psi |
| \nu | 泊松比 |
0.16 |
| p_r | 油藏压力 |
122.45 psi |
| p_w | 油井压力 |
0 psi |
模型属性
仿真结果
对仿真结果进行镜像处理,可由一半分支结的仿真结果得到完整分支结的仿真结果,如下图所示,给出了由压降所引起的总位移和速度场分布图。到目前为止, 我们已知变形最严重的部分恰好位于分支结的正上方区域,但是仍然无法确定该油井是否稳定。
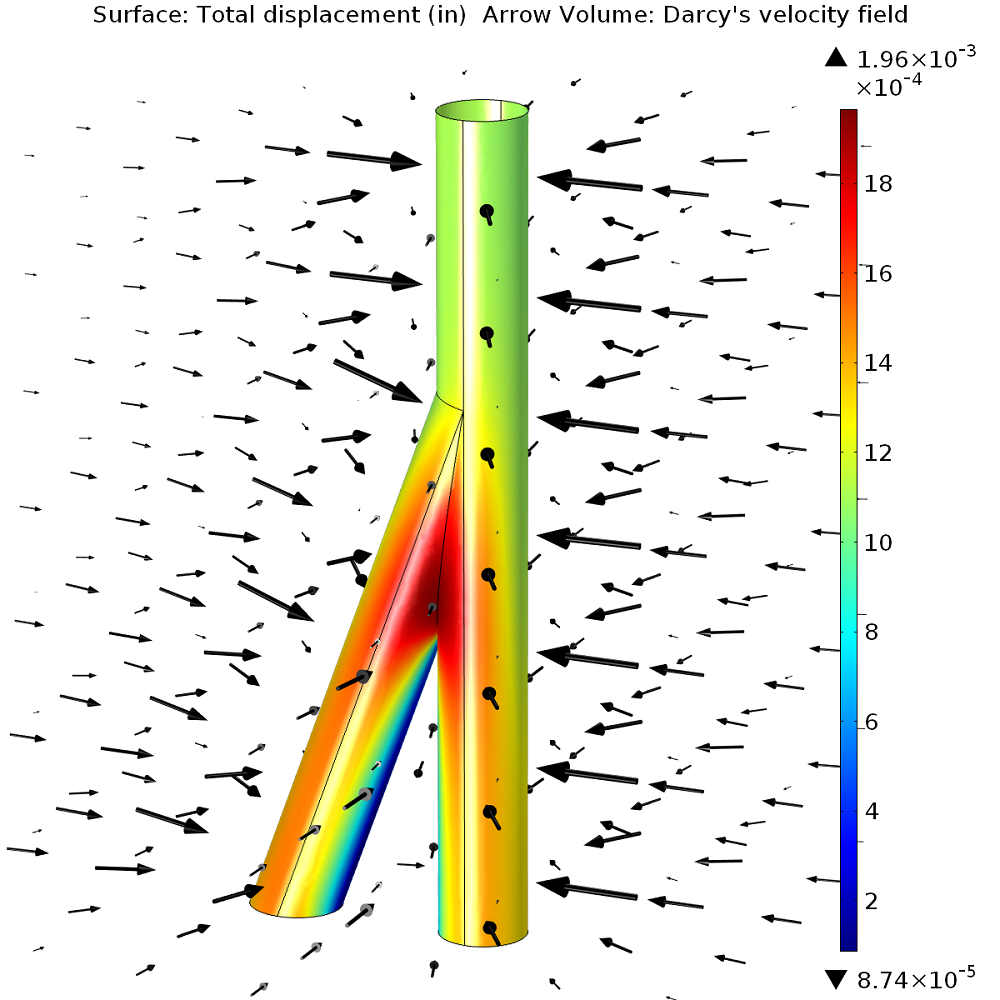
分支结的表面位移(彩图)和速度场(箭头图)分布图。
油井稳定性判定
仿真结果给出了压强变化对油井周围应力和应变分布的影响,需要一个失效判定标准来确定油井稳定与否。3D 库伦准则(线性化Lade准则)与岩石失效的实验结果非常吻合,但是该准则需要额外的校准参数。
该准则下,失效和三个主要应力 (\sigma_1, \sigma_2, and \sigma_3),以及液体压强有如下关系:
其中,
S_0 为库伦凝聚力,\phi 为库伦摩擦角。如果 fail > 0 表示油井是稳定的;fail = 0 表示油井壁的岩石已经碎裂;fail < 0 表示油井会出现大面积坍塌。
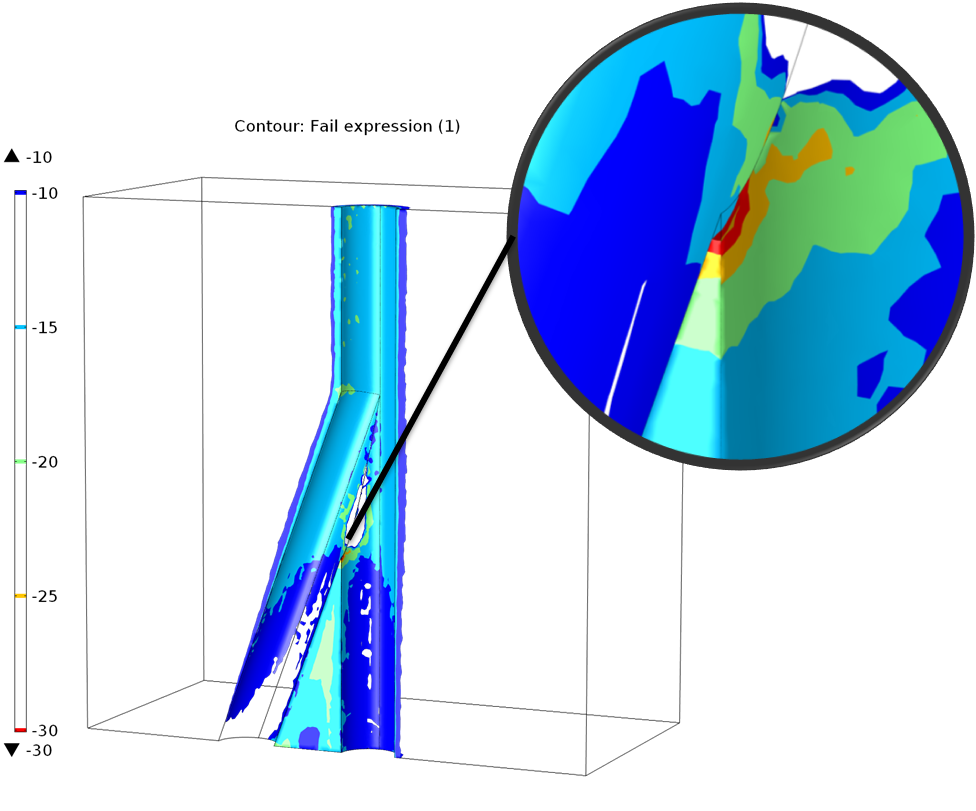
failure 值计算结果,风险最大的位置恰好位于分支结上。
failure值越小,表明失效的风险越大。如前文分析,失效风险最大的地方位于分支结上。如果对油井施加类似套管的支撑力,失效风险将会下降。
下图是对支撑力进行参数化扫描得到的仿真结果,如图所示,支撑力越大失效风险越小。
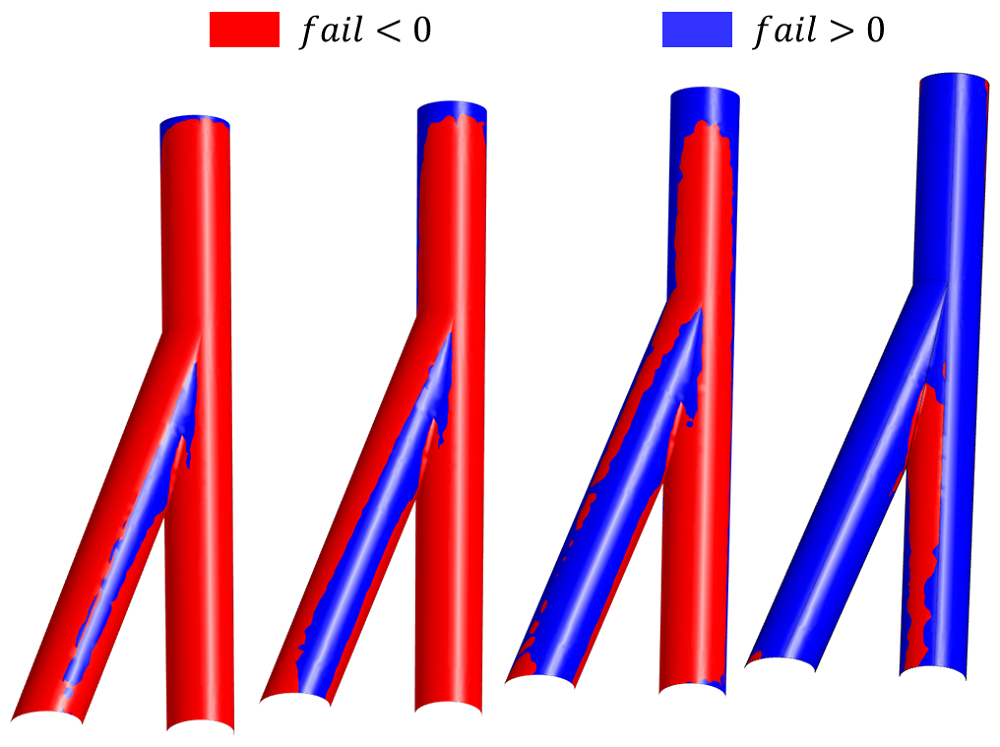
不同支撑力下油井的 failure 值分布图,从左到右支撑力分别为:5e4, 7.5e4, 1e5, 2.5 N/m^2)。
总结和未来仿真方向
本文介绍了如何对多分支井的分支结进行仿真。开放油井的稳定性是非常重要的一个问题,本模型充分展示了如何通过数值仿真来节约成本。稳定性评估是钻井施工前期的工作。
模型假定油井仅发生弹性形变,实际上也可以采用岩土力学模块和结构力学模块。对弹塑性材料进行类似的仿真。也可以进一步考虑温度引起的热膨胀,这在地热能领域是一个非常感兴趣的研究方向。



评论 (0)