带标签的博客文章 CFD 模块

如何基于梯度优化分析冰川流动?
2018年 7月 17日
利用观测参数化数值模型是地球物理模拟的关键。通过一个冰川示例模型了解如何在 COMSOL Multiphysics® 中做到这一点。
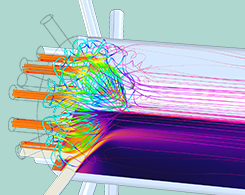
通过仿真优化聚合物生产工艺
2018年 7月 4日
多孔喷嘴管式反应器用于生产聚合物(例如聚酯)。这种类型的反应器中的湍流会影响生产工艺,包括反应动力学、纤维质量、转化率和产率。通过开发充分考虑流体动力学和化学反应的反应器模型,可以优化反应器设计,高效、稳定地生产聚合物。

使用冻结转子近似分析离心泵设计
2018年 6月 25日
当分析离心泵设计时,机械工程师可以使用“CFD 模块”附加的“搅拌器模块”中的“冻结转子近似”。

高效 CFD 仿真的网格划分技术指南
2018年 6月 13日
上一篇博客,我们讨论了生成高质量网格的因素以及如何建立 CFD 模型几何结构来进行网格划分。本文,你将了解物理场控制的网格划分,自适应网格细化以及如何在 COMSOL Multiphysics® 软件中使用不同的网格划分技术执行流体流动仿真。

如何在 COMSOL Multiphysics® 中设置网格进行 CFD 分析
2018年 6月 11日
计算流体力学(CFD)模型的质量通常由求解问题时所采用的网格质量决定。优质的网格有助于模型收敛、降低内存需求,最终得到精确的解。因此,在求解 CFD 问题时,值得我们投入时间和精力认真创建网格。在本篇博客文章中,我们将介绍影响网格质量的各种因素以及如何准备用于网格划分的流体流动模型的几何结构。
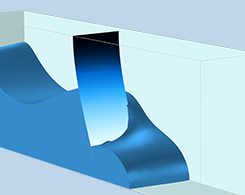
在 COMSOL Multiphysics® 中用动网格为自由液面建模
2018年 5月 31日
您可以使用COMSOL® 软件的动网格功能来模拟没有发生拓扑变化的自由液面。本文为您提供了全面完整的指导。

使用 COMSOL Multiphysics® 模拟自由液面的两种方法
2018年 5月 15日
我们将为您介绍在COMSOL® 软件中模拟自由页面的 2 种方法:水平集法与相场法。了解每种方法的操作方式与优势。

如何求解经典的 CFD 基准问题:顶盖驱动空腔
2018年 5月 8日
我们将演示如何使用COMSOL® 软件求解经典的 CFD 基准问题——顶盖驱动空腔。
