
当声音在尺寸狭小的建筑和几何结构内传播时,热损耗和粘性损耗会导致声波衰减。具体来说,损耗发生在近壁的声-热边界层与粘性边界层中。为了建立与实验测量结果精确匹配的模型,我们需要考虑这一已知现象,并评估这些损耗对热粘性声学系统造成的影响。
热粘性声学简介
对于为小尺寸换能器(例如电容式麦克风、MEMS 麦克风、微型扬声器等)的响应进行建模而言,热损耗和粘性损耗是不可或缺的因素。同类情况还包括分析助听器与移动设备的声反馈,以及研究 MEMS 结构的阻尼振荡。
基于 IEC 60318-4 标准的闭塞耳管模拟器又名 711 耦合器,对其转移阻抗的分析过程如下图所示,这是一个对热电设备进行仿真的良好展示案例。在右图中,分别在加入与未加入热粘性声学损耗这两种情况下对响应进行了模拟。显然,在与标准数据曲线进场对照时,为捕捉正确的特性,我们需要在仿真中加入上述损耗类型。

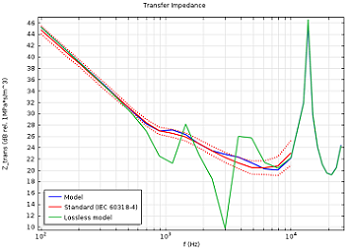
在 7850 Hz 时闭塞耳管模拟器内的压力分布情况(左图),符合 IEC 60318-4 标准。蓝色曲线表示加入热和粘性损耗后的转移阻抗模拟结果,红色曲线为指定标准曲线,绿色曲线表示无损耗模型的结果(右图)。
热声效应通常在共振处最为明显,共振会增强热声效应并降低其频率。为了模拟这些效应,必须在控制方程中加入热传导效应和粘性损耗,并通过 Navier-Stokes 方程、质量(连续性)方程及能量守恒方程求解动量。这一操作是通过求解“声学模块”中热粘性声学 接口的热粘性声学方程来完成的。热粘性声学方程又称粘热声学或线性化的 Navier-Stokes 方程。
在下文中,我们将解释热粘性声学方程的物理背景,并介绍一个关键的边界层特征:长度尺度,同时还会在文章最后列出描述流体介质的必要材料参数及其简要说明。
探究热粘性声学背后的物理场
声波实际上是背景静态(大气)压力场顶部产生的微小线性压力波动的传播。波动控制方程(波动方程或 Helmholtz 方程)的推导,是通过扰动基本的流体力学控制方程(如 Navier-Stokes 方程、动量方程、连续性方程和能量方程)或对其进行线性化 来完成的。这一操作可为任意的微小(声学)扰动生成动量守恒方程、质量守恒方程和能量守恒方程。
许多声学仿真 App 接下来可以通过一系列的假设来简化这些方程。我们假定系统无损耗且等熵(绝热且可逆)。不过如果保留粘性效应和热传导效应,最终会得到用于求解压力、速度和温度的热粘性声学方程。
推导控制方程
在开始推导频域内的控制方程前,首先假设小型谐波振荡具有稳态背景属性。因变量的形式为
其中 p 表示压力,\mathbf{u} 表示速度场,T 表示温度,\omega 表示角频率。
带上标符号(‘)的变量为声变量,带下标 0 的变量表示背景平均流量。
在热粘性声学模型中,假设流场背景为静态,则 \mathbf{u}_0=\mathbf{0}。接着需指定背景压力 p_0 和背景温度 T_0 (它们可以是空间的函数:T_0=T_0(\mathbf{x}) 和 p_0=p_0(\mathbf{x}))。
将上述方程插入控制方程,且仅保留在一阶变量中为线性的项,如此便能得到加入了粘性损耗与热损耗的声波传播的控制方程。
备注:详尽过程请参考 Acoustics Module User’s Guide中的 “Theory Background for the Thermoviscous Acoustics Branch” 章节。
频域内的热粘性声学 接口中的控制方程是连续性方程(删除了全部声变量的上标符号)
其中 \rho_0 表示背景密度;动量方程为
其中 \mu 表示动力粘度,\mu_\textrm{B} 表示容积粘度,右侧的项表示应力张量的散度;能量守恒方程为
其中 C_p 表示恒压热容,\textrm{k} 表示导热系数,\alpha_0 表示热膨胀系数(等压),Q 表示可能的热源;最后可得到与压力、温度和密度的变化相关的线性化状态方程
其中 \beta_T 表示等温压缩率。
控制方程的左侧表示守恒量:质量、动量与能量(实际为熵)。在频域中,与 i\omega 相乘相当于时间的微分。右侧的项表示在方程内局部更改或修正各自守恒量的过程。在其中的两个方程中,具有表示由粘性剪切和热传导而产生的散射损耗的项。如果速度场内存在梯度时,模型会发生粘性损耗;而当温度场内存在梯度时,则发生热损耗。
粘性边界层与热边界层
当声波在壁周围的流体中传播时,固体表面会生成所谓的粘性 边界层和热 边界层。在壁上,我们对速度场施加一个无滑移条件 \mathbf{u} = 0,对温度场施加一个等温条件 T = 0。等温条件是一种非常有效的近似处理方式,因为固体内的热传导通常比流体高出几个数量级。这两个条件可生成由粘性边界层和热边界层构成的声学边界层。体条件下的流体流动几乎无损耗,且可用此边界层条件中的等熵(绝热)条件来进行描述。
下图展示的是时谐波在沿壁的水平面内传播的问题(可以想象成声波在一小段管道内的传播过程)。左图显示速度变化,右图显示由壁到本体的流体温度变化,中间的动画显示了速度幅值以及速度矢量在一段谐波周期内的变化。
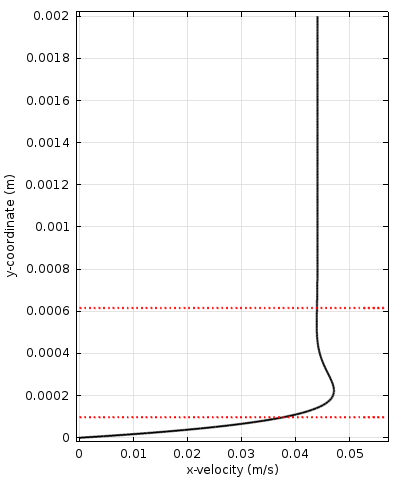
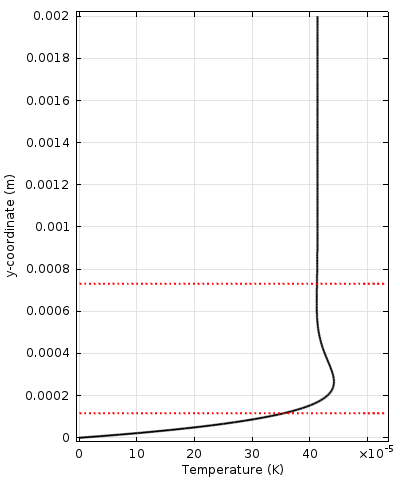
在水平面内传播的声波(下图),及其从壁到本体的速度变化(左图)和流体温度变化(右图)。最靠近壁的红色虚线表示粘性边界层与热边界层厚度。每个图像中较高的红色虚线表示边界层厚度的 2 \pi 倍。动画表示声速分量,颜色图表示速度幅值。
粘性边界层与热边界层清晰可见。有时会将这两个边界层厚度分别称为粘性穿透深度与热穿透深度。因为边界层内具有很大的梯度,因此其中的损耗也相当大。这意味着在尺寸相对较小的系统中,与边界层有相关的损耗将不可忽视。对于许多工程应用(小型换能器、移动设备等)而言,加入与边界层相关的损耗是正确模拟设备物理特性和响应的关键。
在上方的速度和温度绘图中,红色虚线表示粘性特征长度,以及该长度值的 2 \pi 倍(称为粘性/热波长)。两个特征长度的关系可以用无量纲的 Prandtl 数,即 Pr 表示为
此关系式可用于计算系统中粘性损耗与热损耗之间的比。在空气中,该值为 0.7,在水中则约为 7.1。这是因为在空气中,热效应与粘性效应几乎同样重要,然而在水(和其他大多数流体)中,热损耗仅起到较小的作用。粘性边界层与热边界层厚度在“声学模块”中作为用于进行后处理时的预定义变量,分别用 ta.d_visc 和 ta.d_therm 表示。Prandtl 数表示为 ta.Pr。
我们可以通过解析法求解平面波问题,随后可推导出粘性(d_\textrm{visc})边界层厚度和热(d_\textrm{therm})边界层厚度的表达式。它们可通过以下公式计算
在 100 Hz、20 °C、1 atm 的环境中,d_\textrm{visc} 的值在空气中为 0.22 mm,在水中则为 0.057 mm。下图显示了粘性边界层与热边界层在一定频率范围之内的厚度变化。
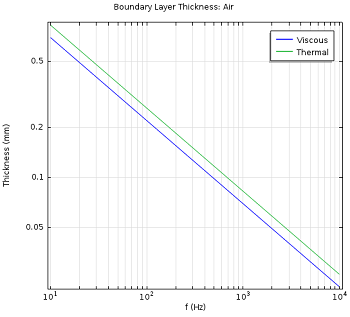
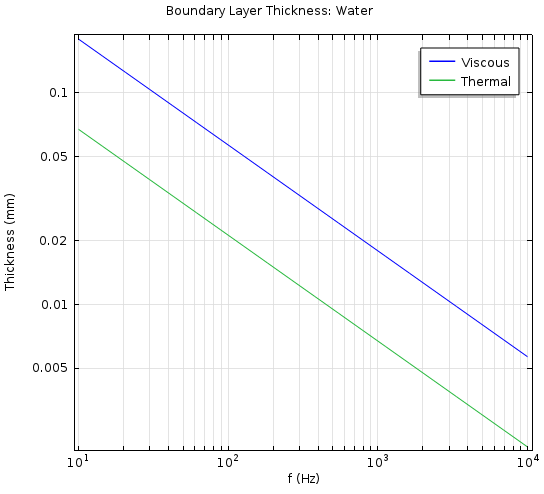
在空气(左图)和水(右图)中,粘性(d_\textrm{visc})边界层厚度与热(d_\textrm{therm})边界层厚度值随频率的变化情况。
图像表明粘性损耗效应和热损耗效应随着声波传播频率的增高而减弱。最后,在使用热粘性声学 接口进行模拟的过程中,我们捕捉到了另一个重要效应,那就是当小型设备处于低频时,绝热声学会过渡到等温声学。这个效应发生在热边界层扩展到整个设备的时候,对 B&K 4133 电容式麦克风等设备十分重要。在等温条件下,声度变成了等温声速。
体损耗、衰减与狭窄区域声学
值得注意的是,粘性损耗与热损耗同样存在于体相流中。当声学信号经过长距离传播并衰减时,通常便会发生此类损耗。声纳信号就是一个例子。在空气中,这些类型的损耗仅在极高的频率下才非常显著(在可听声频率范围内可忽略)。当然,描述体损耗同样使用了热粘性声学的控制方程,因为它们包含全部物理场。不过,使用热粘性声学方程模拟大型域的计算成本过于高昂,您还可以使用“声学模块”中的压力声学 接口,并在粘性、热传导 或热传导与粘性 之中选择一种流体模型。
捕捉全部物理效应需要详尽的细节,因此使用热粘性声学 接口进行模拟的计算成本非常高。当声波在具有恒定截面的波导或圆管中传播时,我们可以使用压力声学,频域 接口中的狭窄区域声学 特征来模拟热粘性损耗。该域特征将与声学边界层相关的损耗均匀地添加到了流体中。在这类情况中,通过解析法推导出来的损耗十分准确。狭窄区域声学 特征能有效减小模型的大小,并可在获得完整详尽的热粘性模型之前便迅速地对结果进行初步评估。
材料参数
求解完整的热粘性声学模型涉及到以下材料参数的定义:
- 动力粘度,\mu
- 动力粘度 \mu 用来度量流体内部抵抗剪切力的阻力的大小。动力粘度是常数,定义为应力与应变速率之比。动力粘度与运动粘度 \nu 的关系为 \mu = \rho_0 \: \nu。动力粘度有时也用符号 \eta 来表示。
- 容积粘度,\mu_\textrm{B}
- 容积粘度又称体积粘性系数、第二粘性系数或膨胀粘性系数。它与因流体的膨胀和压缩而产生的损耗有关。\mu_\textrm{B} 出现在应力张量项中(方程 3 的右侧),该项与体相流的压缩率(\nabla\cdot\mathbf{u})存在关联。这一因素难以测量,往往取决于频率的高低。
- 恒压热容(比热容),C_p
- 恒压热容这一材料参数用来描述流体温度变化所需的热量(恒压条件下)。
- 导热系数,\textrm{k}
- 导热系数是 Fourier 热传导定律中,温度梯度与热通量之间的比例系数。
- 热膨胀系数(等压),\alpha_0
- 热膨胀系数用于描述流体在热作用下的体积扩大现象,反映了温度升高时流体的膨胀能力。
- 等温压缩率,\beta_T
- 等温压缩率是流体状态方程的一个重要参数,用流体内的压力变化与体积变化之比进行表示。等温压缩率与常规(等熵)压缩率的关系可以通过比热率表示为 \beta_T = \gamma \beta_s。
关于热粘性声学理论的结语
我们在上文中讨论了热粘性声学的理论基础与相关方程,接下来将介绍如何使用 COMSOL Multiphysics 及其“声学模块”创建热粘性声学模型。我们将在此系列博客的下一篇文章中结合众多案例和应用介绍相关的操作要点和技巧。
扩展阅读与参考文献
- The “Thermoviscous Acoustics Branch” section in the Acoustics Module User’s Guide of the COMSOL Documentation
- D. T. Blackstock, “Fundamentals of Physical Acoustics”, John Wiley and Sons, 2000
- S. Temkin, “Elements of Acoustics”, Acoustical Society of America, 2001
- B. Lautrup, “Physics of Continuous Matter”, Second Edition, CRC Press, 2011
- P. M. Morse and K. U. Ingard, “Theoretical Acoustics”, Princeton University Press
- A. D. Pierce, “Acoustics: An Introduction to Its Physical Principles and Applications”, Acoustical Society of America, 1989
- A. S. Dukhin and P. J. Goetz, “Bulk viscosity and compressibility measurements using acoustic spectroscopy”, J. Chem. Phys. 130, 124519 (2009)
编者注:本篇博客文章已于 2016 年 7 月 12 日更新,与 COMSOL Multiphysics 5.2a 版本一致。






评论 (0)