
COMSOL Multiphysics 5.0 版本针对传输线改进了“数值 TEM 端口”特征。本特征将二维模型中的阻抗计算应用于三维示例,通过该技术提升了功能。
从二维到三维:计算阻抗
研究传输线的行为时,经常要分析特征阻抗。特征阻抗是指沿传输线传播的波的电压和电流之比。通过计算阻抗,设计人员能修改传输线以改进其传输功率,并减少信号反射。
案例库中包含了有关计算传输线结构中阻抗的示例,重点介绍了两类,同轴电缆和平行导线传输。
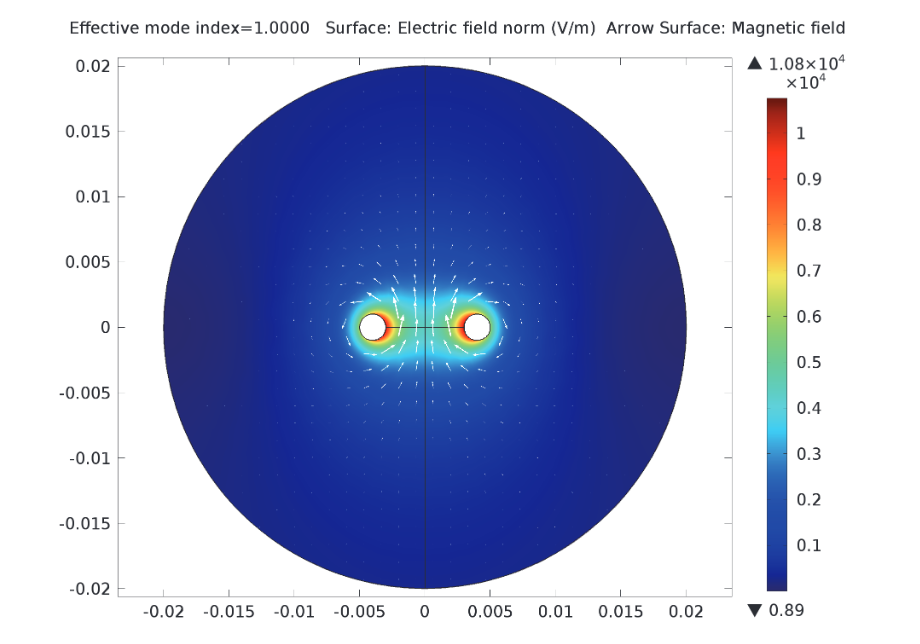
每个模型中的传输线都在 TEM 模式下工作,电场与磁场也都在电缆传播的法向方向。因此,模拟一个二维截面足以计算场与阻抗,模型通过模态分析研究特征来求解。这两个案例中,均将电压作为两个导体之间电场的线积分进行分析。同时,电流等于磁场沿导体边界、或任何切入导体间空间并将其分为两部分的闭合等值线的线积分。
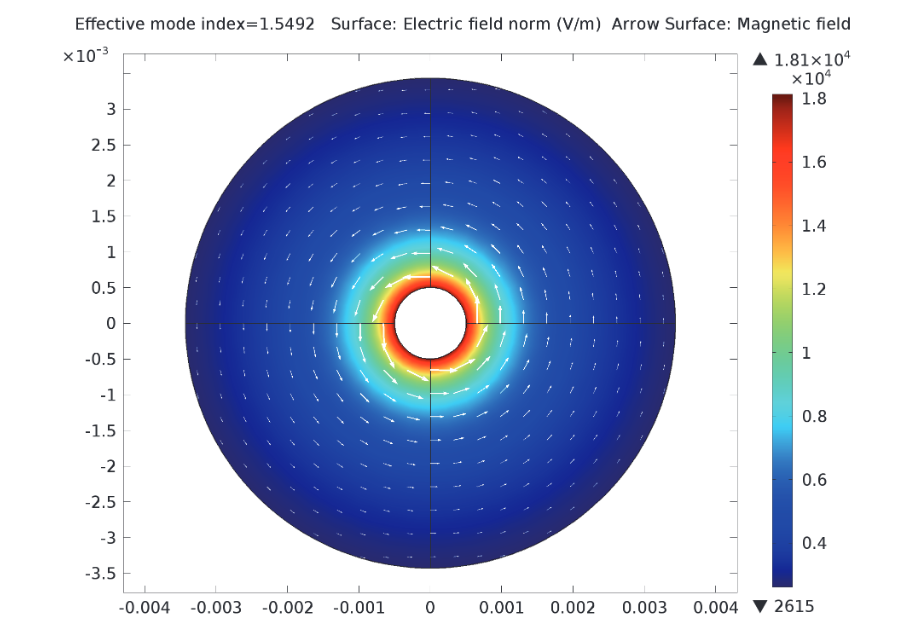
在这些箭头图中,表面代表电场大小,箭头代表磁场大小。左图显示了同轴电缆内的场,右图显示了两条平行导线周围的场。
现在,数值 TEM 端口特征将二维模型中的阻抗计算求解技巧拓展到了三维空间。再加上 COMSOL Multiphysics 5.0 版本中新增的设定和子特征,本特征现可用于计算三维模型中的阻抗。
数值 TEM 端口使用示例
使用开口谐振环的陷波滤波器模型简要介绍了数值 TEM 端口的使用。模型包括一个耦合至微带线的开口谐振环。线圈整体作为陷波滤波器或带阻滤波器使用。
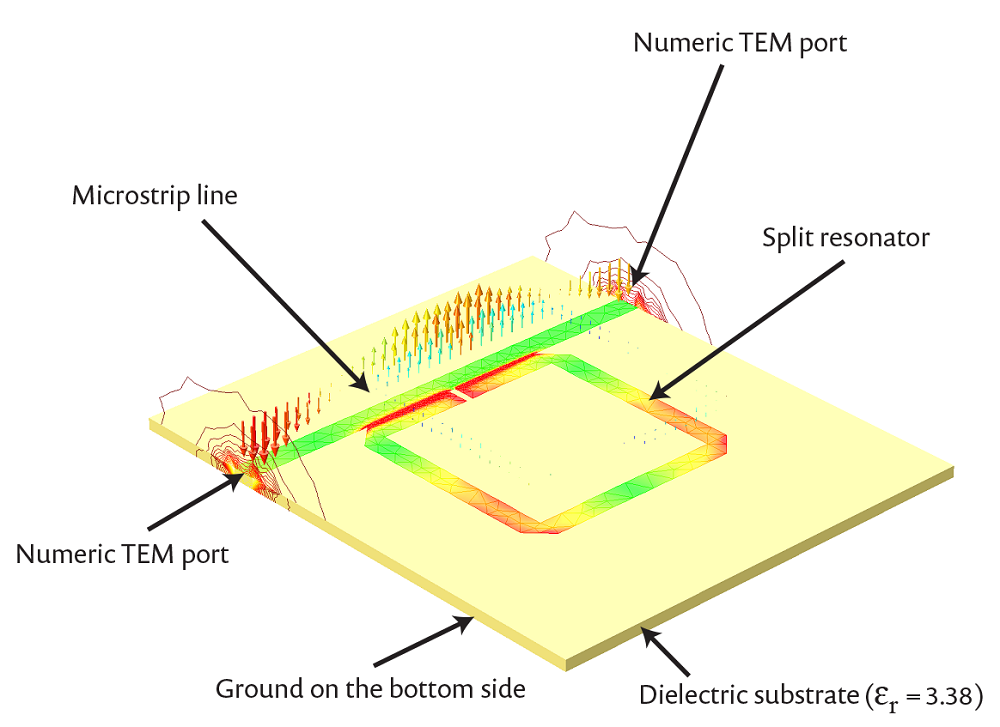
线圈示意图。
为了实现带阻滤波器的响应,开口谐振环部分靠近且耦合到微带线中。印刷开口谐振环位于接地面,具有多个谐振模式。在本例中,我们对接近 2.4 GHz 的频率感兴趣。模型的金属部分处理为完美电导体,模型域中除接地面外的其他外部边界均采用了散射边界条件。其余部分处理为一个真空域。
微带线各端的每个表面均增加了一个数值端口。这些端口被设计为根据边界模式分析来计算结构上的电模式场。选择数值端口设定中的‘作为 TEM 场分析’。该设定要求定义电场与磁场的积分线,以便计算端口的电压与电流。从这些积分线中得到的信息随即用于计算端口的特征阻抗。
计算阻抗与参考阻抗的比率用于表征端口模场。电场存在于两个导体之间,场分量位于传播方向,端口边界法向的场分量可忽略。因此,端口模式可作为横向电磁波 (TEM) 场分析。
下方的第一张图显示了 xy 面上的电场模。绘图显示了所感兴趣的频率(2.4 GHz)下电场沿开口谐振环的对称性约束。
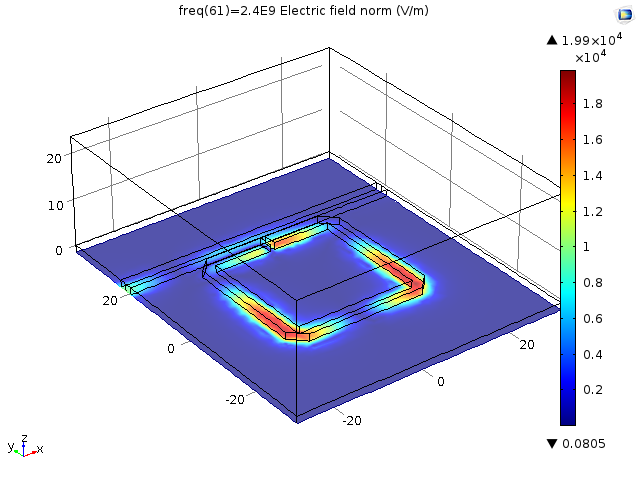
电场模的模型突出了 2.4 GHz 下电场沿开口谐振环的对称性约束。
下一张图展示了器件的频率响应。我们观察到该器件的行为相当于一个带阻滤波器,在 2.4 GHz 附近,S11 接近 0 dB,S21 小于 -10 dB。
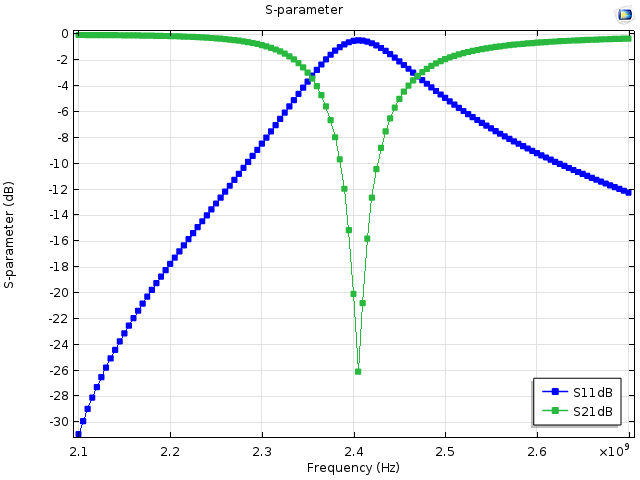
该器件的频率响应绘图显示,他确实可以作为一个高效的带阻滤波器。



评论 (2)
柯 李
2021-11-22如何只计算脊波导的主模分布
Min Yuan
2021-12-07 COMSOL 员工您好,如果只是看主模分布,可以在二维绘图组中查看场强分布即可。如果是查看模场的有效直径或面积大小可以参考下面案例中的“定义-变量”:http://cn.comsol.com/model/fiber-simulator-30421