复合材料是指至少由两种材料构成的异质材料。在不同类型的复合材料中,层状复合材料非常常见,被广泛用于飞机、航天器、风力发电机、汽车、船舶、建筑物和安全设备等领域。COMSOL Multiphysics® 软件的附加产品复合材料模块内置了专用于研究层压复合材料结构的特征和功能。一些常见的层压复合材料有纤维增强聚合物、颗粒增强聚合物、层压板和夹层板等。
编者注:原博客最初由 Pawan Soami 撰写,发布于 2018 年 12 月 6 日。现已更新,以反映最新版本软件的特征与功能。
内容简介
什么是复合材料?
由于复合材料具有特定的力、热、电和磁性能,因此在不同的领域具有许多潜在的应用。例如,一些行业正在开发具有传感、驱动、计算、通信和其他功能的“智能”复合材料。在结构工程领域,复合材料较传统的整体式材料更加坚固和轻盈,因此得到了广泛的应用。在使用这种材料设计复合结构之前,工程师必须充分了解它们的性能。
使用复合材料的优势和面临的挑战
相较于传统材料,复合材料具有多种优势,例如:
- 高强度重量比
- 强耐冲击性
- 高抗疲劳性和抗腐蚀性
- 摩擦性和磨损性增强
- 低导热系数和低热膨胀系数
- 高耐热性
复合材料由多种材料混合而成,因此使用这些材料也会遇到一些挑战,包括:
- 各向异性特性
- 复杂的损伤和失效模式
- 原材料和加工成本高
- 难以重复利用和处置
- 不同组件的连接性差
复合材料的应用领域
由于具有以上优点,复合材料被广泛用于以下领域:
- 航空航天工程(如卫星的机翼、机身和结构板)
- 国防安全(例如,坦克和潜艇)
- 风力发电机(例如,叶片)
- 建筑和施工 (例如,门、面板、框架和桥梁)
- 化学工程(例如,压力容器、储存罐、管道和反应堆)
- 汽车和运输工具(例如,自行车和汽车零部件)
- 海洋和铁路运输(例如,船体和铁路部件)
- 消费品和体育用品(例如,网球拍和高尔夫球杆)
- 电子产品(例如,配电柱和连接箱)
- 矫形辅助工具
- 安全设备
复合材料的类型及其分类
复合材料有多种分类方法,其中一种方法是根据构成类型(即基体和加强件)进行分类。根据基体材料的类型,可以将复合材料分为以下几类:
- 聚合物基复合材料 (PMC)
- 金属基复合材料 (MMC)
- 陶瓷基复合材料 (CMC)
- 水泥基复合材料 (CeMC)
根据加强件类型,可以将复合材料分为以下几类:
- 纤维复合材料
- 晶须复合材料
- 颗粒复合材料
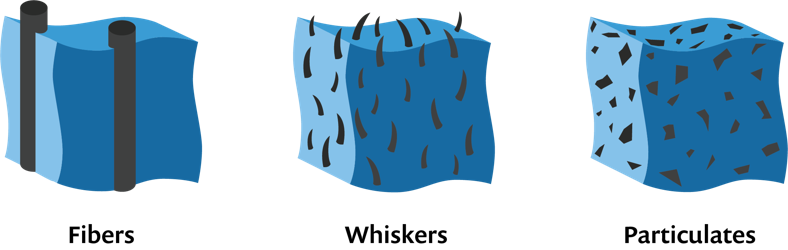
纤维、晶须和颗粒复合材料示例
纤维增强复合材料
相较于其他层压复合材料,纤维增强聚合物(FRP)是当今非常流行的一种复合材料。这些材料通常由作为主要承载元件的长纤维和周围用于支撑纤维并传递载荷的基体组成。纤维以指定的方向排列在材料的每一层(或薄层)。大量这样的薄层铺设在一起就形成了可用于构建结构部件的层压复合材料。工业用纤维通常由碳、玻璃、芳纶或硼制成。根据纤维材料的类型,目前业界最常用的两种纤维增强聚合物是碳纤维增强聚合物(CFRP)和玻璃纤维增强塑料(GFRP),也称为玻璃纤维。
虽然我们可以使用 复合材料模块分析任何各向异性层压复合材料,但在这篇博客中,我们将重点讨论单向纤维增强聚合物。
层压板类型
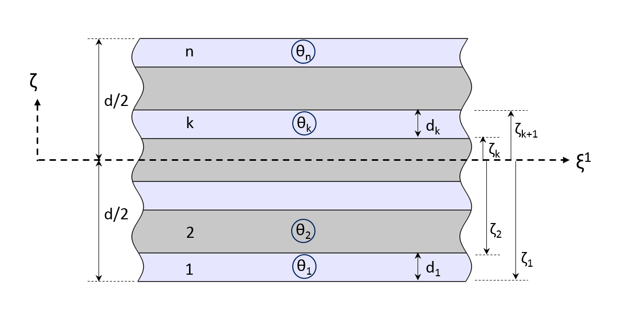
复合材料层压板是指由两个或多个单向层/层/薄片按照指定的方式,以一致或变化的纤维取向铺设而成。薄片可以由相同或不同的材料制成,并且可以具有各自的厚度。铺设顺序由各层纤维相对于层坐标系第一轴的取向定义。
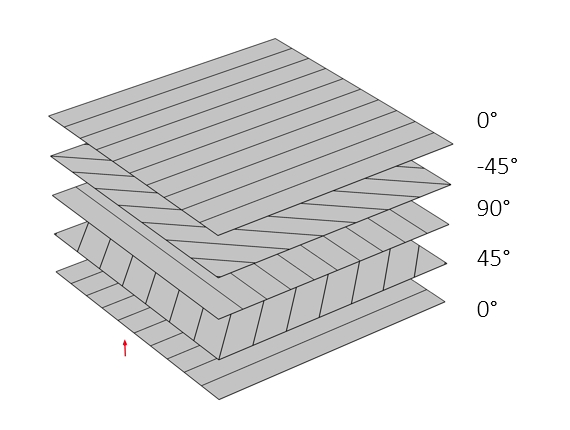
反对称平衡层压板的铺设顺序(0/45/90/-45/0)。
根据铺设顺序,复合材料层压板被分为以下几种类型:
- 斜角层压板 (例如, 45/30/-45/-30)
- 交叉层压板 (例如, 0/90/0/90)
- 对称层压板 (例如, 45/30/30/45)
- 反对称层压板 (例如, 45/30/-30/-45)
由于纤维、板层和层压板的几何比例完全不同,因此分析复合材料层压板相当困难。这也是我们要在细观力学、宏观力学,以及两种(或多种)不同尺度上执行分析的原因。
细观力学
细观力学分析侧重于复合材料的组成层水平。它考虑了组成材料、材料界面以及材料的内部排列。细观力学分析不仅可以计算均质化的材料特性,还有助于了解细观层面的应力、应变、非线性、失效和损伤等。基于细观力学的均质化分析方法主要有两种:
- 分析法(例如,混合规则)
- 数值方法(例如,使用代表性体积单元 (RVE) 或重复单元 (RUC) 进行有限元分析)
在模型开发器树的 材料 节点下,多相材料 和 有效材料 节点包含多个用于分析计算有效性的混合规则。有效材料 节点内置于复合材料模块,包含以下混合规则:
- 体积平均
- 质量平均
- 谐波体积平均
- 谐波质量平均
- 幂律
- Heaviside 函数
- Voigt–Reuss 模型
- 修正的 Voigt–Reuss 模型
- Chamis 模型
- Halpin–Tsai 模型
- Halpin–Tsai–Nielsen 模型
- Hashin–Rosen 模型
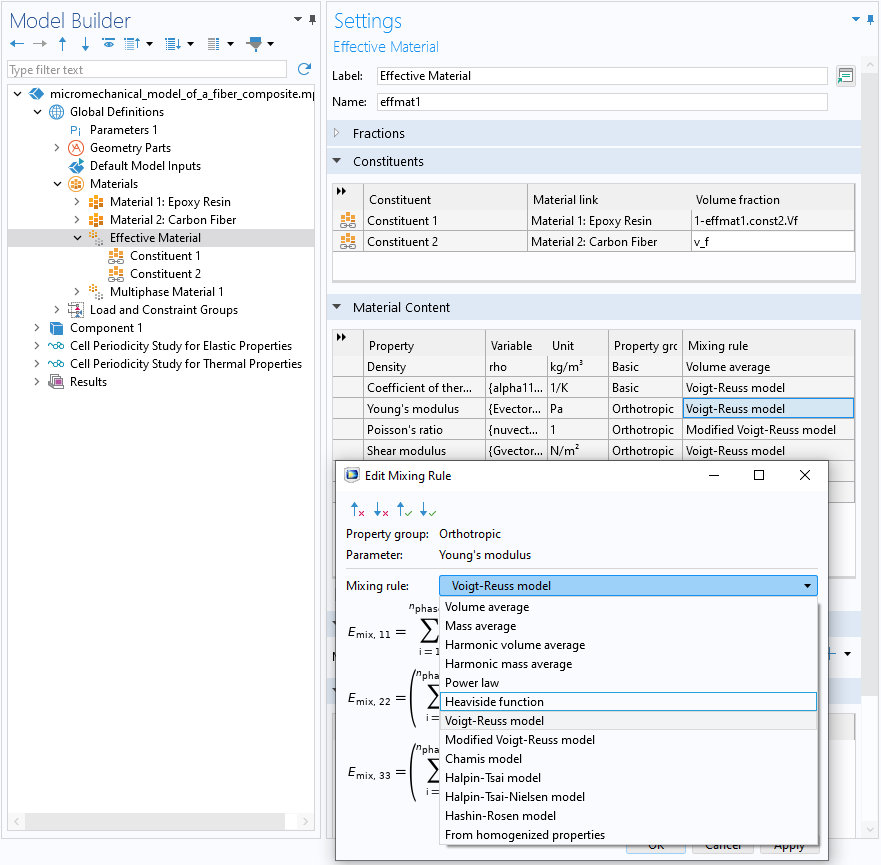
显示了 混合规则选项的 有效材料特征设置窗口
要使用有限元方法数值计算均质材料特性,需要使用 RVE 或 RUC。对于周期性材料,RVE 与 RUC 相同,但对于非周期性材料,RUC 的概念无效,因此必须使用 RVE 材料子体积。

60% 纤维体积分数的纤维复合材料层的晶胞。
在 COMSOL Multiphysics® 中,使用 固体力学 接口中的 单元周期性 节点进行基于细观力学的均质化。该接口有两种不同的边界条件:周期性 和均质。周期性 边界条件适用于周期性材料,需要使用 RUC 材料子体积。对于非周期性材料,可以通过 RVE 材料子卷应用均质 边界条件。在这篇博客中,我们将重点讨论周期性单向纤维复合材料的均质材料特性。
我们从一个包含纤维和基体的晶胞几何结构开始分析。首先需要给出纤维和基体的材料属性。然后,使用单元周期性 节点中的操作按钮设置所需的模型节点和研究。自动创建的研究将计算均质材料的材料数据。
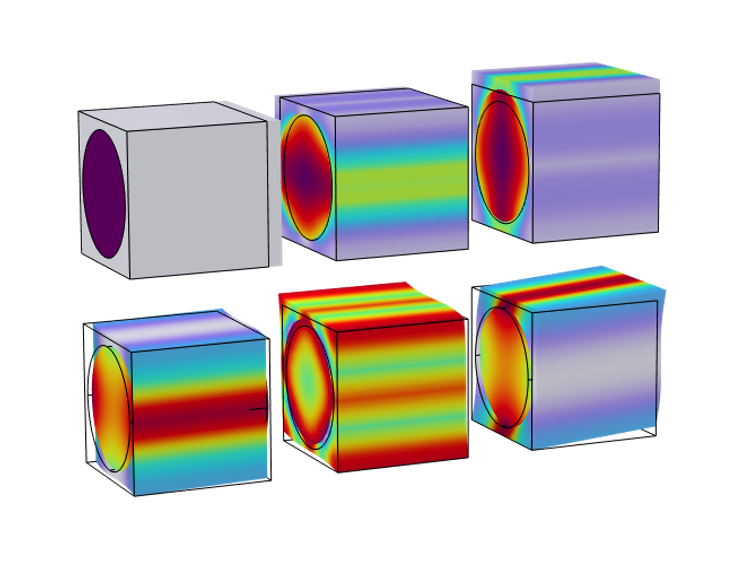
6 种不同载荷下,晶胞中的 von Mises 应力分布和变形。
了解更多内容,请查看纤维复合材料的细观力学模型和复合材料气瓶的细观力学和应力分析案例模型。
宏观力学分析
宏观力学分析基于均质材料确定复合结构的响应。层压板的均质材料特性可通过细观力学分析或实验方法获得。宏观力学分析的目的是计算层状结构在各种载荷和边界条件下的整体响应。宏观力学分析包括以下几个不同步骤。
复合材料仿真的预处理方法
模拟复合层压板, 需要指定以下几个特性:
- 层数
- 每一层的均质材料特性
- 层压板主要材料方向的定向
- 每一层厚度
- 铺设顺序
复合材料层压板的横截面显示了每一层的纤维厚度和取向。
要定义层压材料的属性,需要使用 多层材料 节点。在该节点中,可以添加所需的层数,输入内容可以直接输入表格,也可以从文本文件中加载。指定输入后,就可以预览层压材料的横截面和铺设顺序。您可以将包含层压板定义的多层材料保存在材料库中,方便后续加载使用。
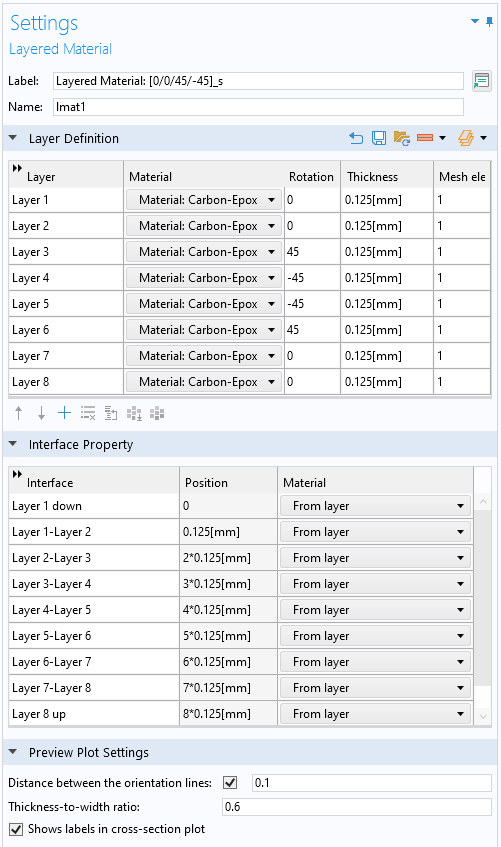
多层材料节点示例。
使用 多层材料 节点定义层压材料后,就可以通过 多层材料链接 或 多层材料堆叠 节点将其连接到几何边界。在此过程中,层压材料坐标系以及几何表面相对于层压材料的位置也会被定义。层压坐标系还能进一步用于解释铺设顺序,创建多层局部坐标系。多层材料链接 和 多层材料堆叠 节点还具有可以将多层材料转换为对称、非对称或重复层材料的更多选项。还包括模拟厚度在空间上变化的模型选项。多层材料堆叠 节点可用于区域建模,在不同的几何选择中,复合材料的铺设顺序会有所不同。
多层材料链接 和 多层材料堆叠 功能的应用示例。
请注意 单层材料 功能是为单层材料设计的特殊的 多层材料 功能。
经典层压板理论和物理场接口
现在,我们已经定义了层压板并将其添加到几何边界上。接下来,我们来介绍经典层压板理论。通常,我们会使用下列三种理论之一分析层压复合壳:
- 等效单层理论
- 经典层压板理论
- 一阶剪切变形层压板理论
- 高阶剪切变形层压板理论
- 三维弹性理论
- 三维弹性理论
- 分层理论
- 多模型方法
一阶剪切变形等效单层理论: 壳接口
在一阶剪切变形等效单层理论(ESL-FSDT)中,计算整个层压板的均质材料特性,并仅在中面上求解方程。该理论采用类壳公式,自由度为网格边界上的三个位移和三个旋转。该理论适用于薄至中等厚度的层压板,可用于计算总挠度、特征频率、临界屈曲载荷和面内应力等全局响应。相较于分层理论,ESL-FSDT 计算成本较低;但对于较厚的层压板,它需要一个剪切修正系数。

ESL-FSDT 理论中的自由度节点。
在 COMSOL Multiphysics® 中,壳 接口的 线弹性材料,多层;超弹性材料,多层 和 压电材料,多层 等多层材料特性都是基于 ESL-FSDT 理论。此外,膜 接口中的线弹性材料,多层功能也是基于等效单层理论,可用于对弯曲刚度忽略不计的极薄复合薄膜进行建模。
在风力发电机复合材料叶片的应力和模态分析案例模型中,风力涡轮机复合叶片是使用 壳 接口模拟的。目标是找出在重力和离心力作用下叶片的表层和隔板的应力分布情况。
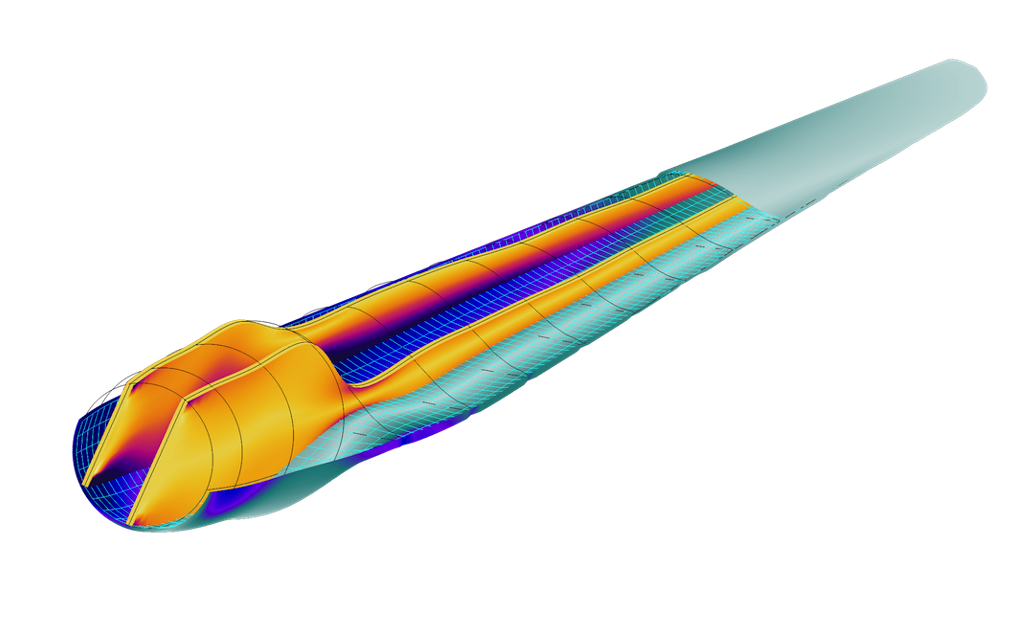
风力涡轮机复合叶片示例。叶片的表层和隔板的应力分布情况。
了解更多内容,请查看以下案例:
分层理论: 多层壳接口
在这个理论中,方程也在厚度方向上求解。因此,它可用于非常厚的层压板,包括分层区域。该理论采用类似固体的表述方式,其中自由度以三个位移的形式分布在厚度方向上。该理论适用于中等厚度到较厚的层压板,可用于预测正确的层间应力和分层,并进行详细的损伤分析。与 ESL-FSDT 理论相比,它支持非线性材料模型,并且不需要剪切校正因子。

分层理论中的自由度节点。
从公式的角度来看,分层理论与三维弹性理论非常相似。但是,相较于后一种理论,它具有以下优点:
- 层压板坐标系和层局部坐标系容易定义
- 面内和面外形函数可以具有不同的阶次
- 无需构建具有许多薄层的三维几何结构
- 面内有限元网格划分独立于面外网格划分
- 分层和界面数据容易处理
在 COMSOL Multiphysics® 中,多层壳 接口基于分层理论。简支复合材料层压板的弯曲案例模型中使用 多层壳 接口和 壳 接口对简支复合材料板进行了弯曲分析,目标是将两种接口得到的厚度应力与给定基准的三维弹性解进行比较。
简支复合板示例。左图:使用 多层壳 接口模拟的板中的 von Mises 应力分布。右图:厚度横向剪应力对比图。
基于此理论的另一个示例,请查看复合材料层压板的强迫振动分析案例模型。
多模型法: 壳接口与多层壳接口耦合
多模型法是将等效单层理论与分层理论相结合,应用于复合材料几何结构的不同部位或不同层,以获得可接受的结果,并优化利用计算资源。除了 多层壳</em > 和 壳 接口外,还需要使用 多层壳-壳连接 多物理场耦合节点将这两个不同的物理场接口在厚度方向上进行耦合。
使用多模型方法分析复合材料叶片案例模型中通过耦合 多层壳 和 壳 接口模拟了一个复合材料叶片,旨在对比不同方法的求解时间。
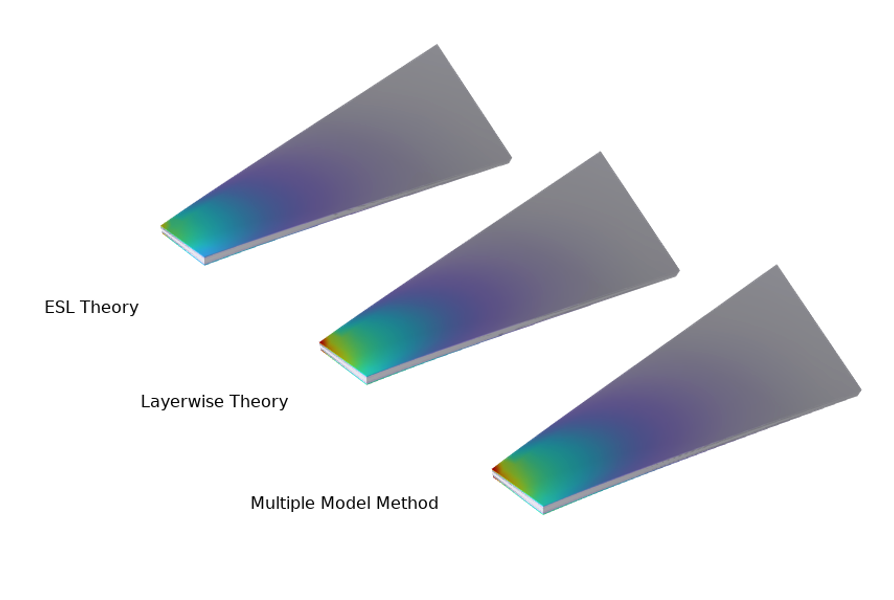
使用不同方法计算的复合材料叶片中的 von Mises 应力分布。
选择合适的层压板理论
基于上述方法,您可以选择合适的层压板理论。一个简单的经验法则是选择基于层压长宽比,即层压板长度与层压板厚度的比值的层压板理论。
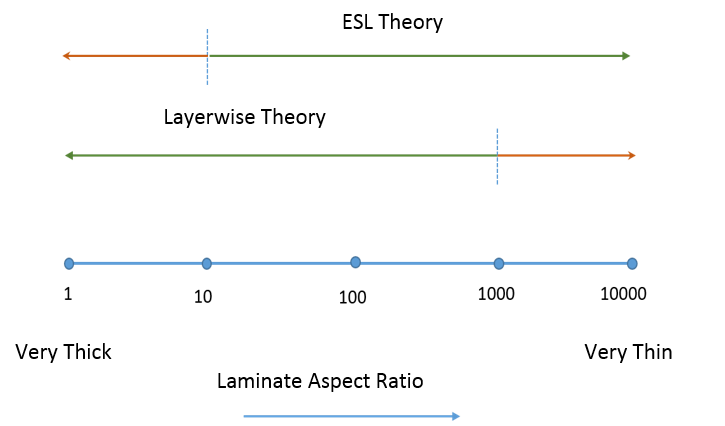
基于层压长宽比的两种层压理论的有效性范围。
材料模型
下表列出了不同物理场接口中用于分析复合材料的材料模型和非弹性效应。
| 材料模型 | 非弹性效应 | 物理场接口 |
|---|---|---|
| 线弹性材料 |
|
|
| 超弹性材料 |
|
|
| 压电材料 |
|
|
您也可以查看正交材料压力容器 – 壳版本和含压电材料的多层壳案例模型,了解更多内容。
损伤、脱层和首层失效理论
许多复合材料都是准脆性材料,在达到临界应力或应变水平后,初始弹性阶段随后进入非线性断裂阶段。当达到该临界值时,裂纹会逐渐扩展,直至材料断裂。裂纹增长导致的材料刚度下降可以通过多层壳和壳接口中的损伤功能进行模拟。目前有两种损伤模型可供选择:标量损伤模型和 Mazars 混凝土损伤模型。此外,还有几种应变软化损伤演变定律可供选择。为避免网格敏感性,可以选择裂纹带 或隐式梯度选项来使用空间正则化方法。
脱层或层间分离是层压复合材料的一种常见失效模式。包括载荷、材料缺陷和环境条件在内的各种因素都可能引发层间分离的发生和传播。要模拟脱层现象,可以使用 多层壳 接口中的 脱层 功能。脱层理论以内聚力模型(CZM)为基础,并包含多个牵引分离定律。要了解更多信息,请查看 COMSOL 案例库中的 复合材料层压板的混合模式脱层和层压壳中的渐进脱层案例模型。
多层壳 接口和 壳 接口的 安全 功能中提供了多种首层失效理论。具体来说,像 Tsai-Wu、Tsai-Hill、Hoffman、Hashin、Hashin-Rotem、Puck 和 LaRC03 等理论在复合材料仿真中非常有用。要了解更多信息,请参阅层压复合壳的失效预测案例模型。
屈曲
使用这两种层压理论中的任何一种都可能产生线性屈曲;不过,与分层理论相比,一阶剪切变形等效单层理论在寻找临界屈曲载荷系数方面更有效。它可以优化层叠结构,以使临界屈曲载荷最大化。更多信息,请参阅复合材料气瓶的屈曲分析案例模型。
多层材料连续性
如果在多层壳 接口所选的几何结构上激活了一个以上的单层材料、多层材料链接 或 多层材料堆叠,那么默认情况下,这些不同多层材料之间的自由度是断开的。使用 连续性 功能可以连接相邻的两个层状材料。利用该功能,您可以对层叠脱落情况进行建模。了解相关建模示例,请参阅 COMSOL 案例库中的复合板的削层模型。
当使用壳 或膜 接口时,自由度只存在于中面上,因此它们在分层材料之间总是连接的。
在并排放置的两块层压板之间设置连续性的不同方法。
A, B, D 矩阵计算
标准刚度和柔度矩阵可通过 壳 接口中的 线性弹性材料,多层 节点进行计算。可用的四个刚度矩阵包括拉伸刚度矩阵 (A)、弯曲-拉伸刚度矩阵 (B)、弯曲刚度矩阵(D)和剪切刚度矩阵(As)。更多详情,请查看层压复合壳的材料特性案例模型。
有时,复合材料层压板的材料特性由 A、B 和 D 矩阵提供。在这种情况下,可以使用 壳 接口中的 截面刚度 材料功能。
复合材料仿真的结果计算工具
在进行宏观力学分析时,COMSOL Multiphysics® 中有多种功能可用于结果计算。下面我们将讨论其中的一些功能。
多层材料数据
由于几何结构只包含表面,多层材料 数据集用于显示有限厚度几何结构的模拟结果。使用该数据集,可以在法线方向上缩放层压板厚度,非常适合分析薄层压板。 多层材料 数据集还提供在以下位置进行计算的选项:
- 网格节点
- 界面
- 层中面
多层材料 数据集包括选择和取消选择多层材料链接或多层材料堆叠中的不同层的选项。其他一些数据集,如镜像、数组、三维截线,三维截点 和 旋转,也可以与 多层材料 数据集一起使用。
体绘图和表面绘图
多层材料 数据集可直接使用不同的体图、表面图、切面图等。
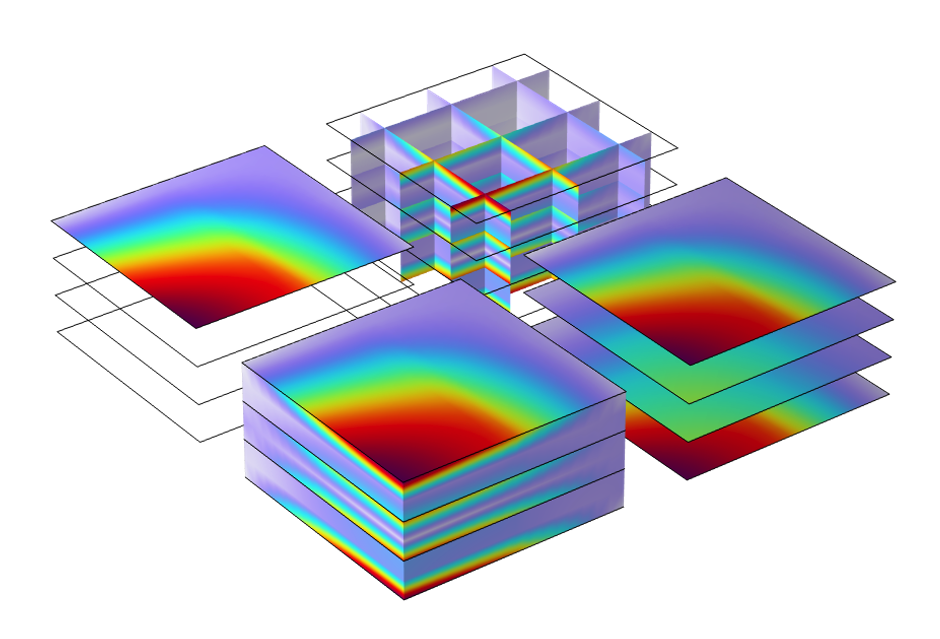
使用 多层材料 数据集绘制的各种结果图。
多层材料切面图
对于复合材料层压板,多层材料切面 绘图在制作切面时提供了更大的自由度。一些有用实例包括创建切面绘图:
- 通过一个或两个层
- 穿过多个(或所有)层(请注意,不需要在厚度方向上放置切面)
- 在层的特定位置,但不在中面上

使用 多层材料切面绘图创建的层压板每一层中面上的 Von Mises 应力。
全厚度图
该绘图用于确定不同量通过层压板厚度上的变化。您可以在边界上选择一个或多个几何点,也可以选择创建切截点数据集或直接输入点坐标。
层压板上某一点横向剪切应力在厚度方向的变化。
线图或点图
要创建特定变量的线图,需要使用基于 多层材料 数据集的 三维截线 数据集。同样,要创建特定变量的点图,也需要使用基于 多层材料 数据集的 三维截点 数据集。另一种解决方案,可以将包含特殊算子的变量与 多层材料 或 解 数据集一起使用。
复合层压材料的多物理场分析
结构连接
在大多数情况下,系统的结构分析需要使用不同的单元类型或物理场接口。下表列出了可用于连接不同结构物理场接口的多物理场耦合。
请查看多层壳与实体和壳的连接案例模型,了解连接壳和结构单元的示例。
热膨胀
可以使用下列物理场接口模拟复合结构中的热膨胀:
- 壳传热
- 壳 或者多层壳
不同物理场之间的耦合通过下列多物理场耦合节点来定义:
- 热膨胀,多层
有关建模示例,请查看案例库中的层压复合壳的热膨胀模型。
焦耳热和热膨胀
复合结构中的焦耳热和热膨胀可以使用以下物理场接口模拟:
- 多层壳中的电流
- 壳传热
- 多层壳
不同物理场之间的耦合通过下列多物理场耦合节点来定义:
- 电磁热,多层壳
- 热膨胀,多层
声 – 复合材料的相互作用
声–复合材料的相互作用可以通过以下物理场接口模拟:
- 压力声学
- 壳 或者 多层壳
声-结构边界 多物理场耦合节点用于定义这两个物理场接口之间的相互作用。
流体–复合材料的相互作用
流体–复合材料的相互作用可以通过以下物理场接口模拟:
- 层流
- 壳 或者多层壳
流-固耦合 多物理场节点用于定义这两个物理场之间的相互作用。
压电 – 复合材料的相互作用
压电 – 复合材料的相互作用可使用下列物理场接口模拟:
- 多层壳中的电流
- 壳 > 压电材料,多层 或者 多层壳压电材料
压电,多层 多物理场耦合节点用于定义这两个物理场接口的耦合。了解更多内容,请参见含压电材料的多层壳教程模型。
压阻 – 复合材料的相互作用
压阻 – 复合材料的相互作用可以使用以下物理场接口模拟:
- 多层壳中的电流压阻壳
- 多层壳
压阻,多层 多物理场耦合节点用于定义这两个物理场之间的相互作用。
集总机械系统 – 复合材料的相互作用
集总机械系统 – 复合材料的相互作用可使用下列物理场接口模拟:
- 集总机械系统
- 多层壳
集总结构连接 多物理场耦合节点用于定义这两个物理场接口之间的相互作用。
复合层压板的优化
复合层压板是一种合成结构,总是有可能在每层材料、每层厚度和铺层顺序等方面对设计进行优化。利用 优化模块 的功能,可以对复合层压板的不同要素进行优化。要了解此类优化,请查看铺层顺序的优化案例模型,其中根据 Hashin 失效准则对复合层压板的铺层顺序进行了优化。
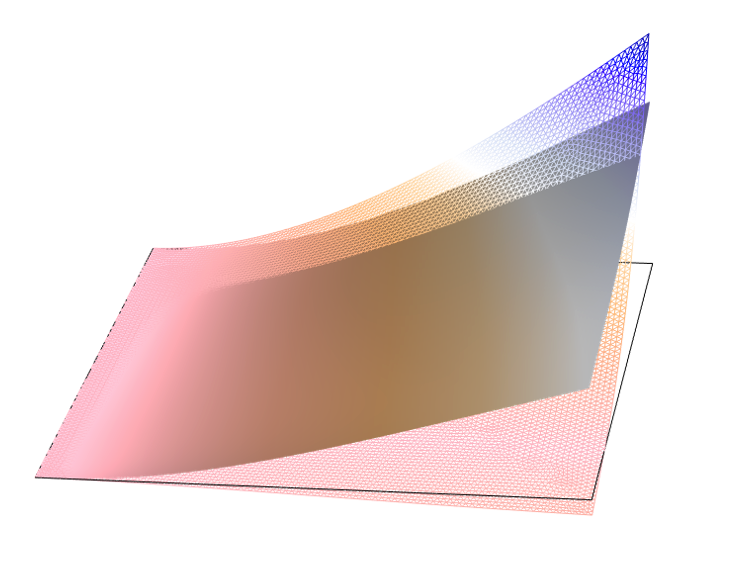
优化后的复合层压板示例。原始布局(线框)和优化布局(实体)的位移。
多尺度分析
复合材料既可以在宏观尺度上进行分析,也可以在细观尺度上进行分析,无论哪种分析都有其优点和局限性。通过宏观和细观分析,可以深入了解复合材料结构及其成分对宏观加载荷的响应。完整的多尺度分析包括宏观分析和每个材料点的细观分析,计算成本高昂。如果我们将分析限制为只包括几个关键材料点,就可以通过使用 固体力学 接口中的 单元周期性 功能和 多层壳 接口进行多尺度分析。
要查看多尺度分析的实际效果,请参阅失效的细观力学:复合材料结构的多尺度分析案例模型。在这个示例中,首先进行细观力学分析以获得均质材料属性,然后使用分层理论进行宏观力学分析以获得全局响应。最后一步是进行细观力学分析,计算局部应力场和应变场以及基于全局平均应变的失效风险。
多尺度分析示例。左图:基于宏观力学分析的复合材料圆柱体应力。右图:使用细观力学分析法测量不同材料点的应力。
下一步
使用复合材料模块,您可以设计、分析和优化由线性或非线性材料组成的多层复合材料结构。要了解有关复合材料模块的更多信息,请点击以下按钮联系 COMSOL。






评论 (1)
乐 张
2025-04-03您好 想请教一下,颗粒复合材料有无可学习的的案例,非常感谢