
等离子体的全局建模是研究大型化学装置的有效方法。在这些模型中,反应由速率系数表示。电子碰撞的速率系数取决于电子能量分布函数(EEDF),该函数通常是非麦克斯韦的,并且可以根据玻尔兹曼方程(BE)的近似值进行计算。在本篇博文中,我们将介绍如何使用 COMSOL Multiphysics® 软件创建一个完全耦合了两项近似的玻尔兹曼方程的全局模型。
建立非麦克斯韦放电的全局模型
因为等离子体反应器中不同数量的空间信息被视为体积平均,所以全局模型中的方程被大大简化了。在没有空间导数的情况下,方程组的数值解变得相当简单,并且计算时间也减少了。因此,在研究包含复杂化学反应的等离子体的广泛参数区域时,全局模型非常有用。
对于在表面没有净质量产生的封闭反应器,包含 k=1,\dotsc,Q 种物质和 j=1,\dotsc,N 个 反应的混合物由 Q-1种物质的质量分数平衡方程描述
其中, V 是反应器的体积, \rho 是质量密度, k 是物质的质量分数 ,A_l 是表面 l 的面积, h_l 是表面 l 的修正因子 , R_s 是表面 l 的表面速率表达式 ,R_k 是物质 k 的体积速率表达式,M_k 是摩尔质量。最后一项的总和是指新产生或消失的物质表面,其中一种物质的质量分数是从质量守恒中得到的。
电子数密度可以从电中性条件获得
其中, n_k 是数密度,Z_k 是电荷数。电子能量密度 n_{\varepsilon} 可以根据下式计算
其中,n_{\varepsilon}=n_e \overline \varepsilon , \overline \varepsilon 是平均电子能量, P_{abs} 是等离子体吸收的功率,e 是元电荷。等式右边的最后一项代表了电子和离子传输到表面的动能,其总和包涵所有正离子和具有表面反应的边界,\varepsilon_e 是每失去一个电子的平均动能损失, \varepsilon_i 是每失去一个离子的平均动能损失,N_A 是阿伏加德罗常数。
上式中,源项 R_k 和 R_{\varepsilon} 是使用代表碰撞影响的速率系数计算的。特别是对于电子碰撞,速率系数取决于EEDF。而 EEDF 通常是非麦克斯韦分布,并且取决于放电条件。实际上,可以通过使用基本碰撞截面数据求解电子玻尔兹曼方程的近似值来获得 EEDF。一旦知道了 EEDF,就可以通过对 EEDF 上的电子碰撞截面进行适当的平均来计算速率系数。
玻尔兹曼方程和二项近似
玻尔兹曼方程用于描述六维相空间中电子整体演化,如下所示
其中, f 是 EEDF,\textbf{v} 是速度坐标, m 是电子质量,\textbf{E} 是电场, \nabla_v 是速度梯度算子,C 是 f 中由于碰撞而变化的速率。
通常,我们可以求解一个相当简化的玻尔兹曼方程。假定电场和碰撞概率是空间均匀的,我们用速度空间中的球坐标表示玻尔兹曼方程,并且 f 在球形谐波中扩展。该序列在第二项之后被截断,所以 f 的两项近似值为
其中,f_0 是 f 的各向同性部分,f_1 是各向异性扰动,v 是速度,\theta 是速度与场方向之间夹角的度数,z 是沿该方向的位置。
通过在稳态下求解,也就是电场和 EEDF 稳定或在高频下振荡,进一步简化了该问题。最后的简化包括使用以下方法将 EEDF 的能量相关性与时间和空间相关性分离
其中,F_{0,1} 是在时间和空间上恒定的能量分布函数,可验证以下归一化
其中,\gamma=\sqrt{2e/m} ,\varepsilon = \left( v / \gamma \right)^2 。
使用上述近似值,经过一些操作,F_0 可以用一维对流-扩散-反应方程式表示
\right) = S
(有关更多详细信息,请参见参考文献1。)
该方程可用于计算 EEDF,并提供了一组电子碰撞截面和约化电场,E/N (电场强度与气体数密度之比)。根据工作条件,可能有必要包括超弹性碰撞和电子-电子碰撞的影响。通常,我们对平均电子能量的输入值感兴趣。此时,我们可以引入拉格朗日乘子来求解约化电场,从而满足以下公式。
一旦计算出 EEDF,就可以由下式计算等离子体全局模型所需的速率系数
其中,\sigma_k 是反应 k 的横截面 。
下图绘制了在 \overline{\varepsilon} = 5eV 的氩气和相应的麦克斯韦下获得的经过计算的 EEDF。请注意,计算出的 EEDF 与麦克斯韦有很大偏离,以及它如何急剧下降到氩气的第一激发能级 11.5eV 以上。在同一张图中,我们绘制了用于激发集总能级(对应于氩气的第一个 4-s 能级)的截面。利用该图中的信息,我们可以计算出激发 4-s 能级的速率系数。
还需要注意的是,该图中计算出的 EEDF 和截面在重叠区域中变化了几个数量级。因此, \overline{\varepsilon}(或 E/N)的较小变化导致速率系数发生了较大变化。此示例适用于氩气,但在许多其他气体中也发现了相同的行为,这也是等离子体具有极度非线性特性的原因之一。
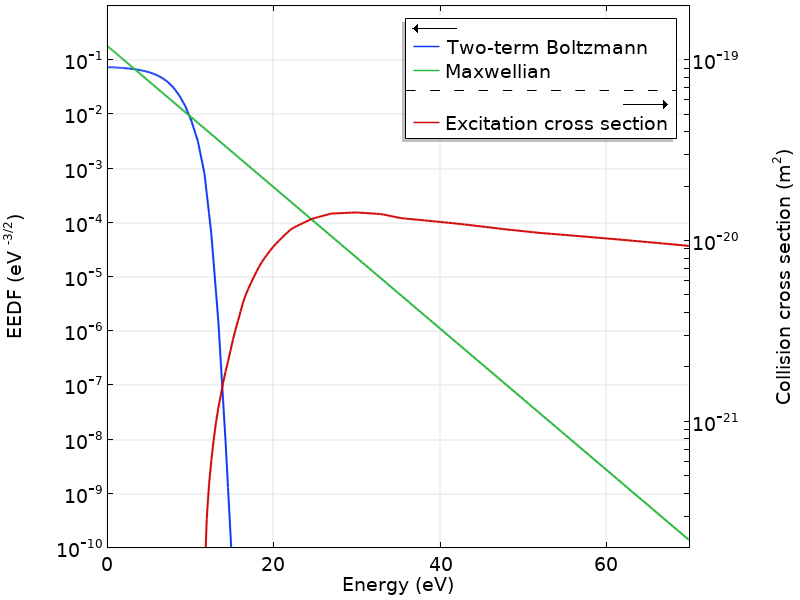
在实际应用中,可以求解二项近似中的玻尔兹曼方程,为全局模型提供速率系数。在这种情况下,每次更改玻尔兹曼方程的输入条件时都会计算 EEDF。
在二项近似中将全局模型与玻尔兹曼方程耦合
本节,我们将展示如何使用 COMSOL Multiphysics 在二项近似中制作与玻尔兹曼方程完全耦合的全局模型。建议分三步进行:
- 创建使用解析EEDF的全局模型
- 使用 EEDF 初始化 研究仅求解 EEDF
- 求解完全耦合的问题
创建 EEDF 初始化研究
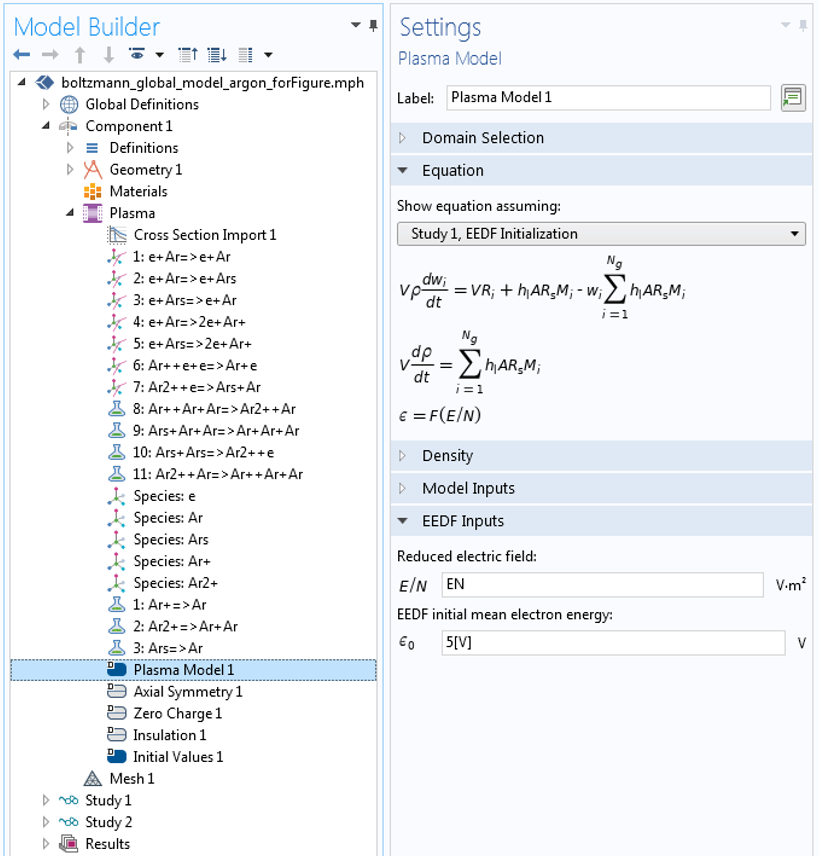
在使全局模型适用于解析 EEDF(步骤1)之后,我们可以进行进一步调查以查看所使用的 EEDF 是否适合需求。还可以通过使用 EEDF 初始化 研究来求解二项近似中的玻尔兹曼方程。该研究步骤求解了电子碰撞截面所需的玻尔兹曼方程以及约化电场或平均电子能量的选择。下面的截图中举例说明了这一过程。首先,在电子能量分布函数设置 栏中,选择玻尔兹曼方程,两项近似(线性)选项或玻尔兹曼方程,两项近似(二次)选项。
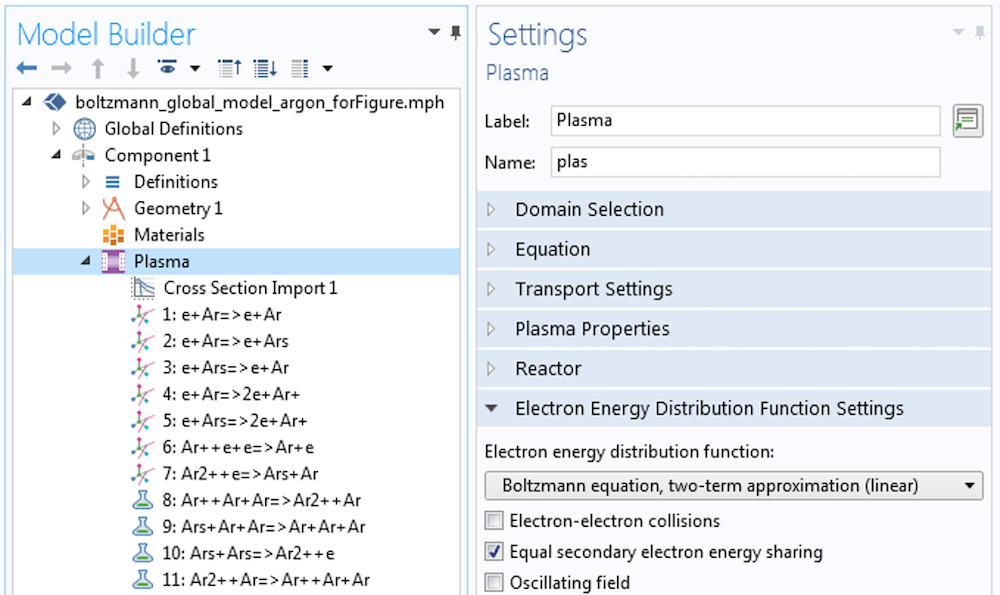
然后,设置约化电场,以便将其用于求解 EEDF。
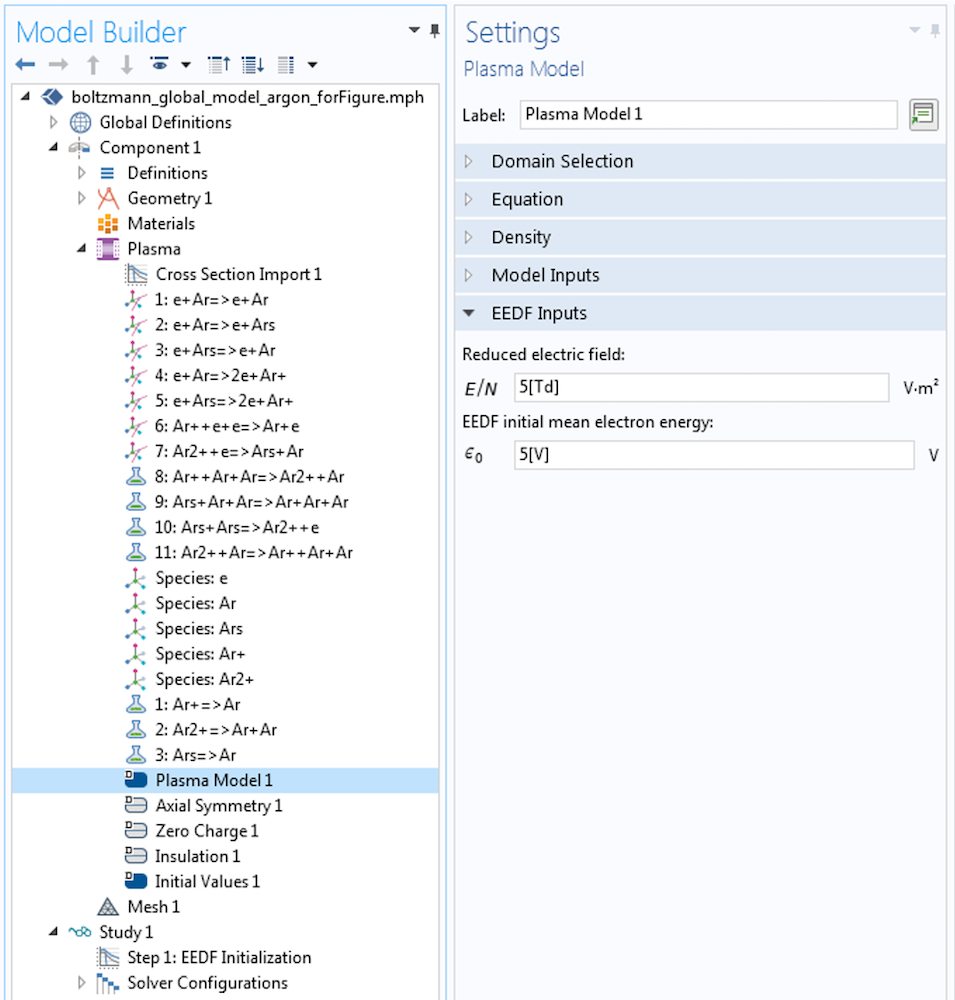
在此阶段,我们可以将计算出的 EEDF 和速率系数与第1步全局模型中使用的进行比较,并评估该模型是否需要进一步改进。如下图所示,如果决定求解完全耦合的问题,请添加另一项研究,并使用 EEDF 初始化 研究的解作为初始条件。要求使用 EEDF 初始化 研究中的解。
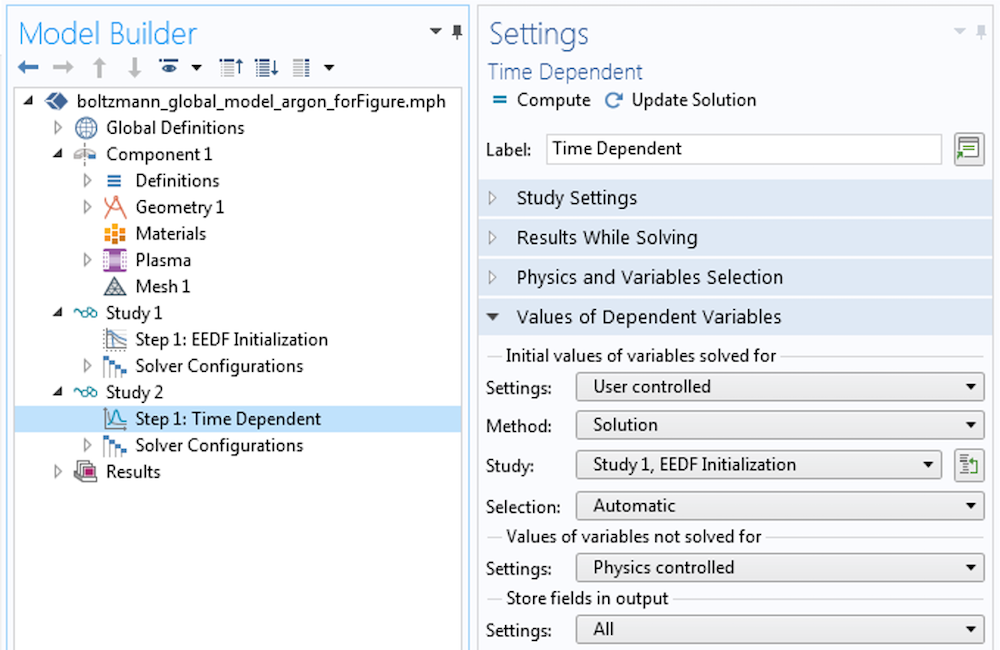
耦合全局模型方程和玻尔兹曼方程
全局模型方程与玻尔兹曼方程之间的耦合可以有两种不同的方式,具体取决于我们是使用局部场近似 还是使用局部能量近似 来定义等离子体特性 部分的平均电子能量。当使用局部场近似时,系统的激励是从约化场给出的。该电场可以是恒定的(可以通过 E/N 进行参数化),也可以来自方程式(例如,电路方程式)的解。当使用局部能量近似值 时,电子平均能量的全局模型方程得以求解,并且等离子体的吸收功率需要由用户设置。在这种情况下,我们发现 E/N 满足以下等式。
示例:由直流电压源维持的等离子体
作为一个实际示例,我们选择对一个 4mm 间隙内由 1kV 的直流(DC)电压源与 100mTorr 的 100kΩ 电阻串联而产生的氩等离子体进行建模。该模型的灵感来自参考文献2。假定该模型没有空间描述,并且使用几何参数和体积平均量来描述间隙中的等离子体。施加到等离子体的电压 V_p,来自电路方程
其中,V_{dc} 是外加电压,R 是电路电阻。
等离子体电流 I_p,是根据下式计算得到的
其中, A 是等离子体的横截面积, \mu N 是约化电子迁移率。
求解 E/N, 得到
其中, d 是电极之间的间隙距离。
如下截图所示,如果我们选择使用局部场近似,则上述 E/N 方程可以在 EEDF 输入栏直接使用。
如果我们选择使用局部能量 近似,则等离子体吸收的功率在平均电子能量 栏可以被定义为
如下图所示。
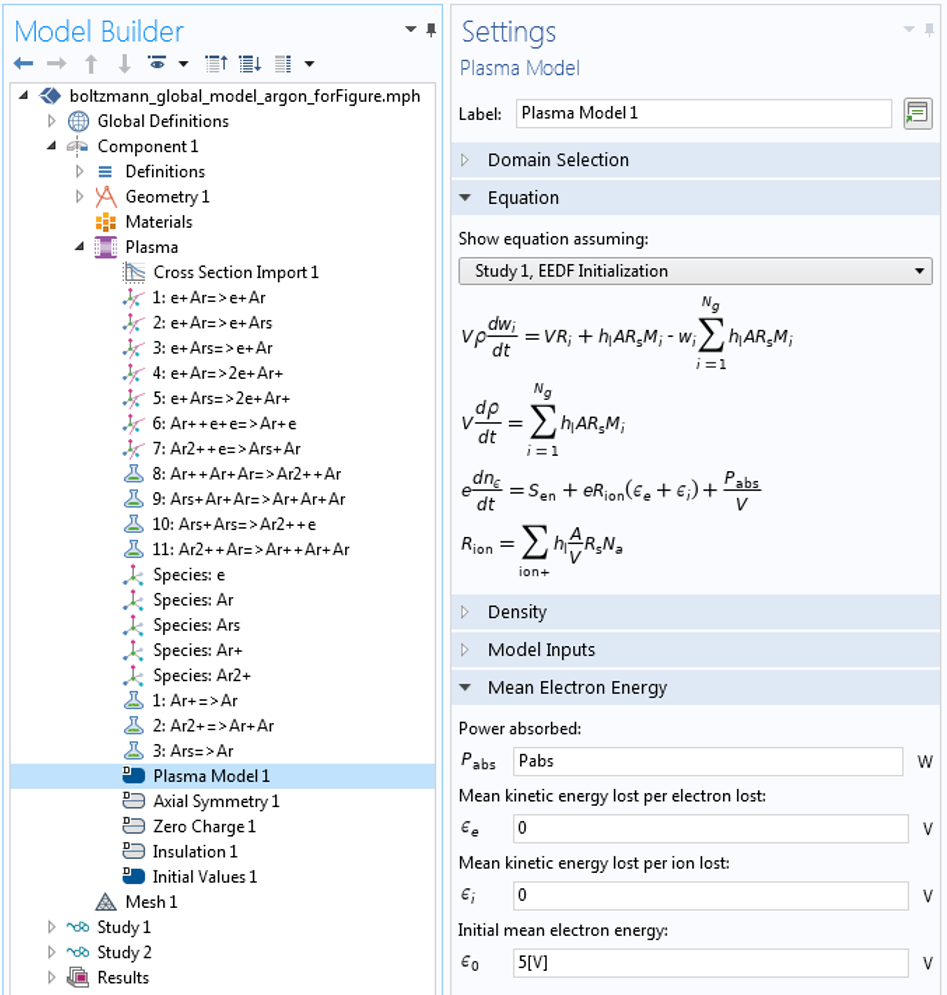
在此模型中,两种方法都给出了非常相似的结果,这是因为在玻尔兹曼方程和平均电子能量方程式中考虑了相同的碰撞事件中的电子能量损耗/增益,并且由于平均电子能量中不包括对壁的能量损耗。
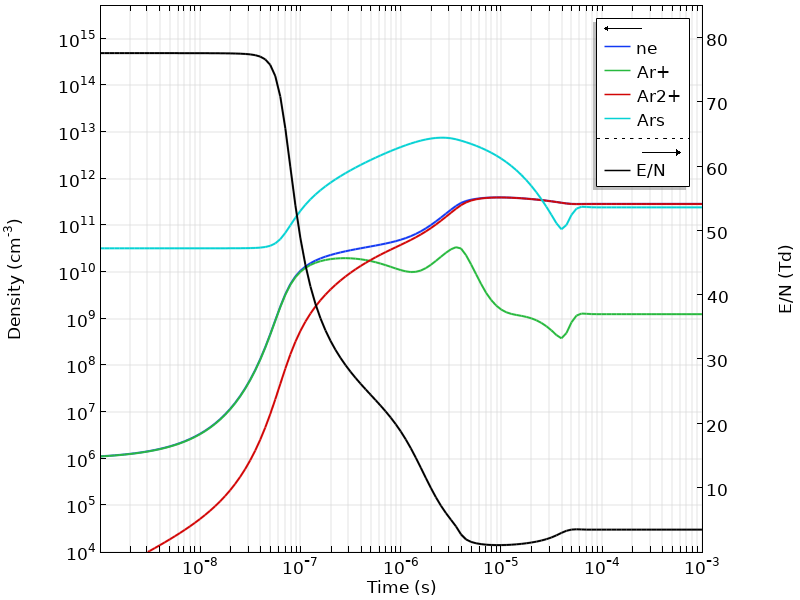
下图显示了带电物质的时间演变和约化电场。最初,间隙中没有等离子体,电场(黑线,右轴)保持恒定值。当击穿开始发生时,带电的载流子和流入电路的电流会迅速增加,从而导致间隙上的压降。在此瞬间状态之后,等离子体达到了一个稳定状态,在此状态下等离子体仅以 4Td 的约化电场维持。
EEDF 的时间演变如下图所示。最初,由于有必要促进等离子体击穿,因此EEDF高于 15eV。在等离子体形成之后,由于电场的降低,电子群冷却下来,EEDF 形成了一个斜率更陡的尾部。随着时间的流逝,并且随着氩激发态密度的增加,EEDF中超弹性反应的影响变得明显,高能量端出现了凸起。请注意,此动画中的时间变化以对数刻度显示。
后续操作
如果想尝试自己模拟本博客文章中的示例模型,请单击下面的按钮,进入 COMSOL 案例库。您需要使用有效的软件许可证,以下载分步说明文件。此外,您还可以下载该模型的 MPH 文件。
您还可以在以下博客文章中阅读有关等离子体物理建模的更多信息:
参考文献
- J.M. Hagelaar and L.C. Pitchford, “Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models,” Plasma Sources Science and Technology, vol. 14, pp. 722–733, 2005.
- Pancheshnyi, B. Eismann, G. Hagelaar, and L. Pitchford, “ZDPlasKin: A New Tool for Plasmachemical Simulations”, The Eleventh International Symposium on High Pressure, Low Temperature Plasma Chemistry, 2008.



评论 (0)