在进行光学设计分析时,不仅要考虑光强,还要考虑偏振。精确操控光偏振可以滤除不需要的光源,极大地提高图像质量,例如,最大限度地减少眩光。了解和操控光偏振的一个有用的方法是利用菲涅尔棱体。借助 COMSOL Multiphysics® 软件,工程师可以模拟菲涅尔棱体和类似单元对光学系统中光偏振的影响。
操控线偏振光和圆偏振光
19 世纪初,因在光学领域的研究和发明而闻名的 Augustin-Jean Fresnel 是第一位将光描述为线偏振、圆偏振或椭圆偏振的科学家。在线性极化平面电磁波中,电场的两个横向分量的相位相同。我们可以将这些分量看作正弦或余弦函数,它们在同一位置达到最大值,也在同一位置降为零。下图显示了线偏振波的波形;波本身的电场显示为黄色,x 和 y 分量分别显示为红色和绿色。

线偏振平面电磁波。
将上图所示的线偏振波与下图所示的圆偏振波进行比较。电场的 x 和 y 分量大小相等,但偏移了 90° 相位延迟。因此,当一个分量达到最大值或最小值时,另一个为零。最终的效果是这两个分量的总和具有类似螺旋的形状,因此被称为“圆偏振”。
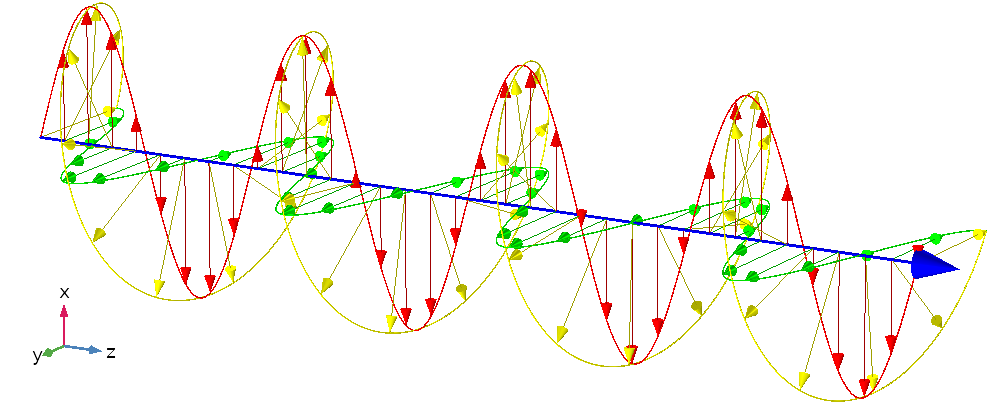
圆偏振平面电磁波。x 和 y 分量分别以红色和绿色显示。传播方向用蓝色显示,总电场幅度用黄色显示。
菲涅尔对线偏振和圆偏振辐射的发现支持了他的假设,即光是一种纯横向波(没有纵向分量),这意味着电场和磁场的振荡总是垂直于传播方向。通过进一步研究光偏振,他解释了光的全内反射不会像之前认为的那样使入射的线偏振光去偏振,而是将其变为椭圆或圆偏振光。全内反射产生的圆偏振光可以很方便地通过一个玻璃平行六面体来证明,其中光线在两个相对的面上发生全内反射——这种设置现在被称为菲涅尔棱体。
菲涅尔棱体 是一种操控光偏振的玻璃棱镜。入射光是以与入射平面成 45° 角入射的线偏振光。然后光在两个不同的面上产生全内反射。每一次全内反射都会导致在入射面和垂直于入射面的电场分量之间产生 45° 的相位延迟,总相位延迟为 90°。因此,出射光是圆偏振。
通过使用 COMSOL Multiphysics® 软件及其附加的射线光学模块,工程师可以预测光在光学系统中传播时的偏振。这是因为射线光学模块使用了 Stokes-Mueller 算法或简单的 Mueller 算法来记录光强度和偏振,它可以完全表示任何偏振状态。下一节,我们将介绍一个教程模型,该模型演示了一个特定入射角在菲涅尔棱体中将光从线偏振变为圆偏振。
使用 COMSOL Multiphysics® 模拟菲涅尔棱体
菲涅尔棱体几何形状是一个简单的未镀膜玻璃棱镜,呈平行六面体形状。下图是一个简单的几何图形。
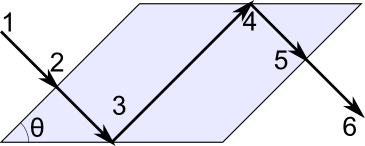
线偏振光(1)进入棱镜(2)。这束光与入射平面成 45° 线偏振——也就是说,位于屏幕中并垂直于屏幕的电场分量具有相等的幅度,并且它们是同相位的。棱镜有一个角度(θ),如果设置得当,它将在全内反射的每个实例(3 和 4)期间导致正交电场分量之间的 45° 相位延迟。然后,光离开棱镜(5)。出射光(6)现在是圆偏振的。位于屏幕中并垂直于屏幕的电场分量仍然具有相同的幅度,但它们的相位现在相差 90°。
在未镀膜表面上由全内反射引起的相位延迟的确切值取决于表面任一侧的折射率 n1 和 n 2,以及入射角 θ。这些量与相位延迟之间的关系可以由斯涅尔定律和菲涅尔方程推导出来。(有关方程的更多详细信息,您可以查看Fresnel Rhomb 模型文档。)
\left(\frac{\cos\theta\sqrt{\sin^2\theta – \left(n_2/n_1\right)^2}}
{\sin\theta}\right) = 45^{\circ}
该模型由两项研究组成。首先,求解给出所需相位延迟 45°的 θ 值。然后,使用该角度定义射线光学模拟的几何形状。
研究 1:求解入射角
首先,可以使用全局常微分方程和微分代数方程接口求解上述方程,在折射率比为 n = 1/1.51 的每个全内反射期间,导致 s 偏振和 p 偏振分量之间相位延迟 δ = 45° 的入射角。(即使这个方程不是常微分方程或微分代数方程,仍然可以使用这个接口来求解。)在这个例子中,θ 值是 0.84855 弧度或 ~48.618°。
研究 2:追踪射线的路径
接下来,可以使用几何光学 接口来追踪射线通过菲涅尔棱体的路径,因为它以 全局常微分方程和微分代数方程 接口计算的入射角进行全内反射。请注意,在这个过程中,光是线偏振的,其偏振方向与入射平面成 45° 角。
从研究 1 获得的入射角值(0.84855 弧度)可用于设置菲涅尔棱体的模型几何形状,这是一个平行四边形拉伸成的 3D 几何形状。首选使用 3D 几何,因为它有助于说明射线偏振状态,因为 3D 射线轨迹 图可以显示偏振椭圆。在这个步骤中,沿每条光线轨迹计算的斯托克斯参数用于描述光的线偏振或圆偏振程度。
评估模拟结果
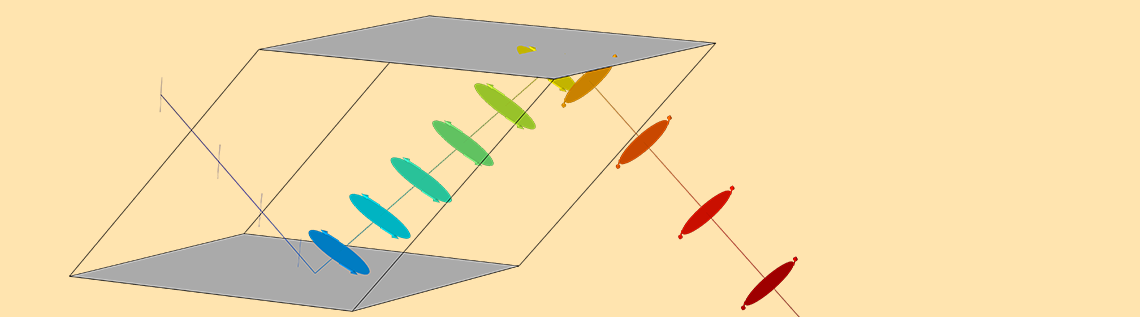
现在,我们来仔细看看前面提到的射线轨迹 图中的模拟结果。在该图中,线偏振射线从棱镜的左侧进入。颜色表示沿射线的光程长度,沿射线路径的圆形和椭圆表示偏振。沿每个圆/椭圆周边的箭头显示瞬时场矢量的旋转方向。
当光穿过菲涅尔棱体时,线偏振射线在经过一次全内反射后变为椭圆偏振。在两次全内反射之后,椭圆偏振变为圆形,这意味着光是圆偏振的。
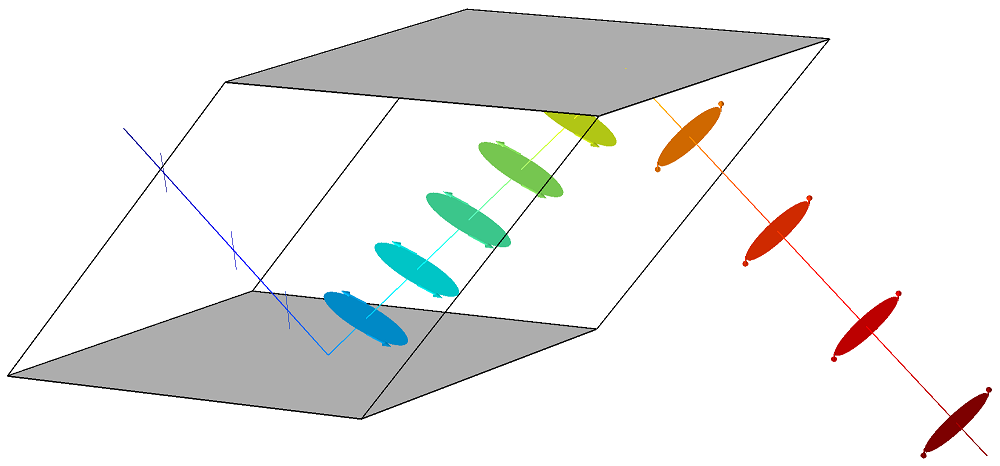
菲涅尔棱体中的射线传播。
在这个摄像角度,出射光是圆形的可能并不明显。但是通过旋转图形窗口中的 3D 图,就可以看到光从线偏振变为椭圆偏振,再变为圆偏振。
动画显示了入射光在菲涅尔棱体中的线偏振(δ = 0),一次反射后的椭圆偏振(δ = 45°),以及两次反射后的圆偏振( δ = 90°)。
可以通过绘制斯托克斯参数的比率,以另一种方式可视化这种偏振,结果如下图所示。首先,光是线偏振的,比率为零。在第一次全内反射之后,该比率的值在 0 和 1 之间,表明椭圆偏振程度不同。然后,在第二次全内反射 之后,幅度几乎完全一致,与圆偏振更加吻合。
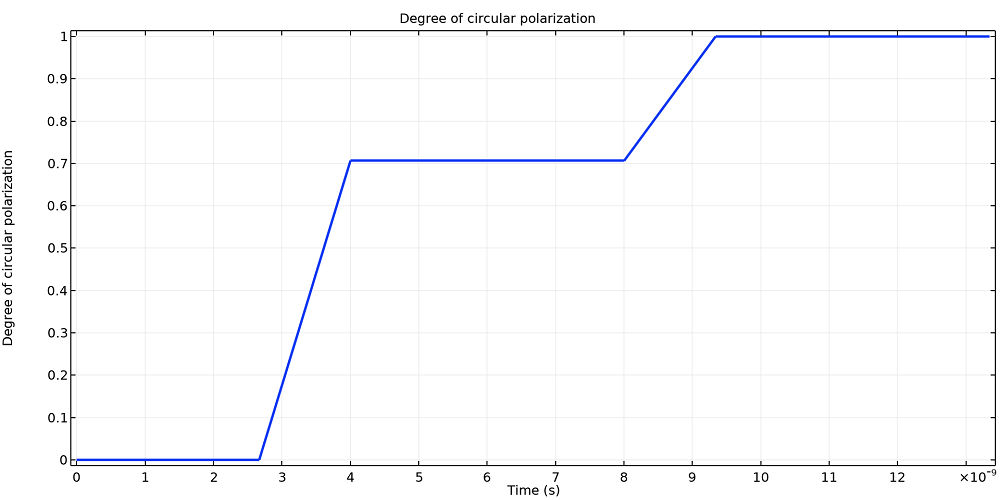
将第四和第一斯托克斯参数的比率绘制为光程长度的函数。
后续步骤
想要尝试模拟本文中介绍的菲涅尔棱体模型吗?请单击下面的按钮,然后,在 COMSOL 案例库中下载此示例的详细分步教程文档和随附的 MPH 文件。
菲涅尔棱体教程的一个自然扩展是在棱镜表面应用薄介电涂层。介电涂层会影响界面处的菲涅尔系数;因此,它们会影响面内和面外电场分量之间的相位延迟。全内反射薄膜无色散移相器(TIRTF APS)就是一个相关示例。它通过薄膜抵消玻璃中折射率的频率依赖性,从而使出射光在很宽的波长范围内保持圆偏振。
扩展阅读
想了解更多关于射线光学仿真的信息吗?请阅读下面这些博客:






评论 (0)