建立子模型：如何分析大型模型中的局部效应

计算机辅助工程（CAE）可以帮助我们在制作物理原型之前，了解机械系统是如何工作的。为了正确地反映真实的系统，我们会在模拟、验证或优化的过程中不断增加建模的复杂性。改进模型的一个简单的建模技巧是，通过增加有限单元的数量来创建更多的评估点。但是，计算机硬件和仿真时间可能会限制模型的大小，因此我们必须寻找其他的解决方案，比如说子模型。

子模型的概念

很多时候，在数值模拟中，为了正确地指定边界条件，我们需要对一个大型结构进行建模。然而，我们要模拟的关键部分可能只占模型的一小部分区域。对于这些情况，子模型 技术将很用。

在建立子模型中，首先分析整个模型的行为。通过网格，可以将边界条件和载荷适当地转移到整个模型上。换句话说，场变量、位移和温度的结果在全局范围内应该是合适的，但导数（如应变）的结果可能在局部 不准确。

第二步，从全局模型中切出关键部分。切割边界应该离关键点足够远，这样全局模型的结果才具有很好的代表性。下图显示了如何建立一个车轮轮辋的子模型示例。在左边的全局模型中，红色矩形框表示需要在子模型中被重新分析的关键部分，右边子模型中的紫色表示切割全局模型的界面。

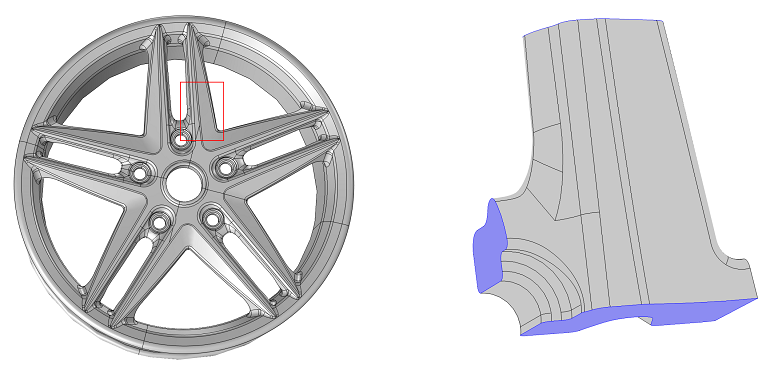
一个车轮轮辋的完整模型和子模型。

将切割界面上的场变量指定为边界条件，可以将全局模型的结果指定给子模型。在 COMSOL Multiphysics 中，我们可以使用广义拉伸 算子来完成这个设置，它可以将模拟结果从一个几何体转移到另一个几何体。由于子模型是完整模型的一小部分，我们可以用更细的网格对其进行建模，使关键部分获得更高的精度。最后一步，在相同的载荷工况下对子模型与全局模型进行解析。当然，在同一个全局模型中也可以有几个子模型。

轮辋的结构分析

我们可以使用多种 CAD 程序来创建几何结构，然后通过 CAD 导入模块或选择一个适用于 CAD 的 LiveLink™ 产品，将几何结构导入 COMSOL 中。当分析一个复杂的几何体时，这种方法很强大。COMSOL 模型库中的轮辋模型就是一个很好的复杂几何体示例。这个模型包含许多细节，为了正确求解多个圆角处的应力梯度，一个数值表示需要许多单元。对于这样一个复杂的模型，我们可以使用子模型技巧来分析局部效应。

首先，我们对完整模型进行分析。不是所有的细节都是用细网格划分的，所以局部结果的精度很低，至少应力是这样。然而，在轮辋的大多数区域，几何是相当光滑的，结果也令人满意。从完整模型的分析来看，最高的应力出现在轮辋背面的一个圆角处，即轮辐和轮毂之间，车轮与车辆在此处相连。接下来，将在子模型中对这个关键部分进行分析。从全局模型中切割一块包含关键点的区域作为子模型，该区域的边界远离关键点，点上的位移具有良好的精度。将全局模型的解设置为切割区域的边界条件，并在关键圆角处使用细网格求解子模型。

全局模型和子模型的 von Mises 应力的比较。全局模型低估了约 20% 的应力。

轮辋模型还展示了如何在分析周期性模型时减少求解时间。轮辋可以分为五个周期单元，每个单元有一对辐条对。当轮辋滚动时，载荷在轮辋周围传播。我们将利用这种几何和载荷的周期性来分析子模型。在全局模型中，只模拟了整个载荷的 1/5。这意味着辐条对 1 承受的载荷在其中心和紧随其后的辐条对之间移动，而辐条对 2 承受的载荷在前面的辐条对和它自己的中心之间移动。另一方面，辐条对3承受的是从前面的第二个辐条对移动到前面的第一个辐条对的载荷。这是通过一个双循环将全局模型的结果应用到子模型的。

对于第一种情况，是对辐条对数进行循环分析，而第二种情况是对载荷情况进行循环分析。在对每个辐条对数进行分析时，我们改变了广义拉伸 的表达式，以便将正确的辐条对模拟结果指定为子模型的边界条件。这可以通过规定一个纯旋转来轻松完成：

其中，$n$ 是辐条对数，$u$ 和 $v$ 是位移，下标 $\mathrm{S}$ 和 $\mathrm{G}$ 表示子模型和全局模型。

实质上，这意味着通过挑选不同辐条的模拟结果，可以获得子模型的整个载荷周期，因为它们承受了不同的载荷条件。

微电子元件中的热疲劳

微电子元件由多个部分组成，例如印刷电路板（PCB）、焊点、电阻器和芯片。焊点将芯片与 PCB 连接起来，具有双重功能。一方面，它将芯片固定住，另一方面，它还为电流创造了一个连接。很少有材料具有完美的结构、热和电性能，而且材料模型是高度非线性的。它们具有蠕变或塑性特性，会发生弹性变形。用非线性材料建模时的一个挑战是分析时间的增加。除此之外，还需要多次迭代；必须求解添加了额外的自由度单独方程，代表每个积分点的非弹性应变。对于三维模型，除了用于弹性分析的3个位移自由度之外，还要使用7个额外的自由度。此外，如果正在处理一个多物理场的应用，除了结构研究外，还需要在模拟中包括热分析或电分析，这需要引入额外的 自由度。

COMSOL 案例库中提供了一个包含详细说明的黏塑性焊点的热疲劳模型，在这个教程模型中，两个芯片被几个焊点连接到一个 PCB 上。当接通电源时，芯片产生的热量会扩散到模型的其他部分，并流向周围环境。由于电源是连续打开和关闭的，因此会出现一个问题，即芯片是否会因热疲劳而失效。这个应用是用子模型技术来模拟的，因为如果对焊点进行高精度模拟，这个模型将非常大。

首先，我们对完整的模型进行了热力学耦合分析。因为我们只需要温度场，而不需要它的导数，所以在用较粗的大网格建模时，热模拟结果也有很好的准确性。最初的结构分析不会在焊点处给出足够的精度，特别是在焊点和周围材料的界面上。选择粗大的网格获得的应力精度较低，黏塑性定律与应力存在非线性关系。在焊点中使用粗大的网格，对其进行疲劳评估，来确定关键的焊点。使用 Darveaux 模型（一个基于能量的模型）预测疲劳寿命。疲劳寿命预测的准确性不足以得出定量的结论，但其结果可用于识别关键点，我们可以在第二个子模型步骤中对结果加以改进。

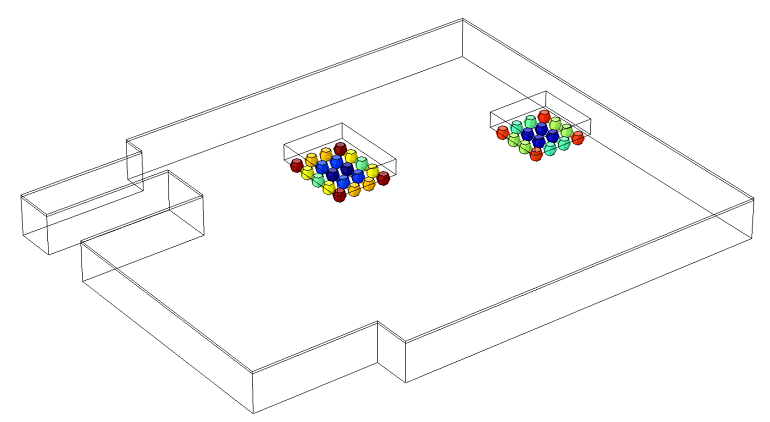
黏塑性焊点的疲劳寿命。红色代表短疲劳寿命，蓝色代表长疲劳寿命。关键的焊点位于球栅阵列角落处较大的芯片下面。所有四个角落的焊点的疲劳寿命基本一致。

一旦确定了关键焊点，就可以创建子模型了。子模型包含了关键焊点以及芯片和 PCB 部件。通过一个广义拉伸 算子将全局模型的结构分析结果应用到子模型的边界上，该边界是在完整的几何形状中进行切割。通过热膨胀将热模拟结果直接应用到整个模型中，并且也可用于非线性材料模型中。这是可以做到，因为全局模型的热结果具有足够精度。通过这种方法，我们将最初的多物理场 分析简化为单一 物理场分析。最后，我们用精细的网格来求解子模型，获得关键部件的应力和疲劳寿命的精确结果。

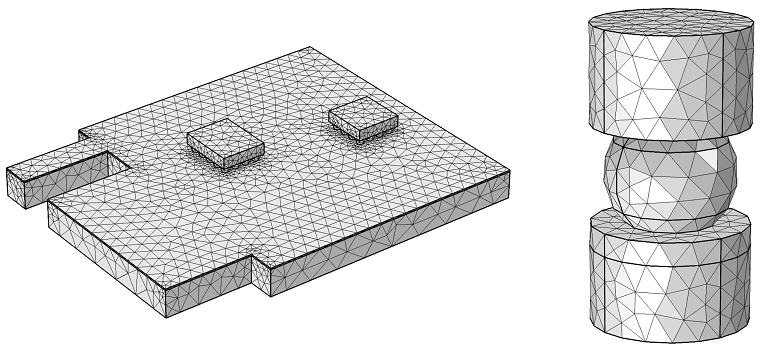
全局模型和子模型网格的比较。全局模型由 300,000 个自由度组成，而单个焊点的子模型由 100,000 个自由度组成。

一些子模型示例

最后，我们分享两个子模型示例。这两个模型需要使用不同的产品建模，因此在不同的模块案例库中都可以找到。

• 结构力学模块的案例库中的轮辋子模型。
• 疲劳模块案例库中的球栅阵列中的热疲劳子模型，同时也使用了非线性结构材料模块。