Menu
封面图片

声学简介

   声学 

什么是声学？

声学是研究声音的物理学，研究内容包括声信号的产生、传输和检测等所有与之相关的多物理学科。这里提到的声音不仅仅是人耳能够听的声音，还包括次声波和超声波；即频率低于和高于人类听觉范围的声波传播。不仅如此，声音的定义还包括在空气以外的介质中的传播，可以是固体中的弹性波（振动），液体中的压力波（如水声学），也可以是多孔材料中的组合传播（多孔弹性波）。

对于人类来说，对声音的最佳理解是将其视为一种感觉，通过耳朵感知声压 p 在某个静态值上下非常微小而快速的变化，这个静态值为大气压（在海平面上约为 10 万帕）。这就是听力，人耳能够检测到的压力微小变化的幅度大约介于 20·10-6 Pa（听阈）到 600 Pa（喷气发动机噪音）之间。通常人类语音的幅值约为 0.02 Pa。一般将幅值以对数分贝刻度给出，相对于 20·10-6 Pa（或 20 µPa）的听阈进行定义（单位为 dB SPL）。这种对数刻度很自然地可以将声音按照人类听觉系统感受响度的方式进行分类。声压级 定义如下

(1)

其中， 为测得的均方根（RMS）声压， = 20 µPa 为空气中常用的参考压力（也称 RMS 值）。在水声学中，通常使用 1 µPa 作为参考值。

下图给出了不同情况下的典型（宽频带）声压级示例。在指定声压级时，指定参考压力、与声源的距离、测量的带宽以及可能的加权函数非常重要。根据经验，每当与声源的距离增加一倍时，声压级下降 6 dB。这称为反距离定律。

显示人类听觉分贝刻度的示意图，范围涉及从耳语到喷气发动机噪音。 分贝刻度，演示了不同情况下的声压级。这些值是在声源附近测量的典型宽频带值（如果没有另行说明）。 分贝刻度，演示了不同情况下的声压级。这些值是在声源附近测量的典型宽频带值（如果没有另行说明）。

波既可以传播，可以驻留，也可以是两者的组合。下图显示一个驻波和一个行波，其中波峰表示压力最大值，波谷表示压力最小值。

驻波（上）和行波（下）的表示图。

波的传播速度为声速 （SI 单位：m/s），其值与传播声波的材料本身的压缩率 （SI 单位：m2/N 或 1/Pa）和密度 （SI 单位：kg/m3）有关，用 表示。空气中的声速约为 343 m/s，水中的声速约为 1485 m/s。具体的取值取决于环境温度、压力，以及其他变量。

为了更好地理解驻波和行波的性质，将与波相关的空气分子的运动进行可视化可以直观地说明问题。下图以另一种形式演示了驻波（上）和行波（下），背景色表示压力幅值（红色为高值，蓝色为低值），其中的点表示与波相关的空气运动。（提示：您可以仔细观察其中一个较大的点，以便更好地理解它的运动情况。）

请注意，即使是行波，空气分子也不会产生向右的净移动。如果发生向前运动，通常是传递与波相关的能量的脉动，单位时间内通过截面传递的能量称为波的强度 （SI 单位：W/m2）。



驻波（上）和行波（下）的压力（红色为高值，蓝色为低值）和空气分子运动表示图。

更笼统地说，声音是流体受到某个源的扰动时产生的，比如音响系统中的扬声器纸盆等物体的振动。当低音扬声器纸盆发出频率非常低的声音时，我们可以观察到它的运动。当纸盆向前移动时，它会压缩前方的空气，使空气压力升高。随后，当它向后移动超过其静止位置时，会使空气压力下降。这一过程不断持续，从而辐射出一种以声速传播的、高低压交替出现的波（参见下面的动画）。


扬声器驱动器产生的声波，红色表示高压，蓝色表示低压。为了方便演示，其中夸大了扬声器纸盆的运动。

频率 f（SI 单位：Hz = 1/s）是每秒感知的振动次数（压力峰值），波长 λ（SI 单位：m）是两个波峰之间的距离。可供参考的数据是，人类听觉系统（对于新生儿）可以感知频率约为 20 Hz 到 20,000 Hz（或 20 kHz）之间的声音。比较常见的频率表示法是使用倍频带或分数倍频带。这是一个对数变换，从生理学上讲，人们采用这种表示法源于这样一个事实：人耳本身会过滤（通过听觉滤波器）声音，并且感知的声音可以用对数频率轴表示。这也是音乐中使用的一个基本概念。同样，人耳也有对数灵敏度，因此，我们使用分贝刻度来表示声压级，如前所述。

简单的数学模型

在数学上，我们使用标量波动方程来描述声波沿一维空间和时间的传播

(2)

这是一个偏微分方程（PDE），其中 t 表示时间，x 表示空间坐标，c 表示声速，p 表示压力（因变量）。

该方程基于几种假设，由连续介质力学的守恒定律（质量守恒、动量守恒和能量守恒）导出，下文将对这些假设进行更详细的讨论。一维波动方程的通解由下式给出

(3)

其中 为任意函数，符号可以确定波是正向运动还是反向运动。

实际上，最常用的通解是此类函数的线性组合，当我们考虑初始条件时，可将其称为达朗贝尔公式。这样的解是一个传播的正弦波

(4)

其中 为波幅。

对于最后一个表达式，通常可以方便地定义波的角频率 （SI 单位：rad/s），即 ，并将频率与完整的 360o 相移关联起来。波数 （SI 单位：rad/m）定义为 ，我们通常将它定义为一个矢量，使其还包含波的传播方向相关信息。一般来说，角频率 与波数 之间的关系称为色散关系；对于简单的流体，关系式为 。上面的动画描绘了一个行波示例，其振荡周期定义为 ，声速为频率 与波长 的乘积。

与频域中建立的波动方程等价的方程是非常重要的亥姆霍兹方程。我们可以通过多种方式来推导该方程：将压力展开为其傅里叶分量，或等效地使用分离变量法（时间和空间）。最简单的方法是假设压力是以下类型的时谐信号

(5)

其中， 是该问题的复值因变量。

将此表达式插入波动方程并将其重新排列，可以得到时谐信号的亥姆霍兹方程（具有恒定的材料参数）

(6)

亥姆霍兹方程常常是对声学问题进行数值分析或解析分析的基础。为了求解波动方程或亥姆霍兹方程，我们应该将这些方程与描述所研究物理问题的材料参数、边界条件和初始条件相结合。有关基本声学的更多详细信息，请参见参考资料 1-4 和下面的“控制方程的详细推导”一节。

声学范围

在声学中，声音由传播介质产生、在其中传播并受其影响，最终被人们检测、感知并进行分析。声信号传播过程的描述涉及许多不同的科学分支，包括工程、地球科学、生命科学和艺术。

例如，音乐家用钢琴演奏出美妙的音符（音乐）；有些工程师研究拾音麦克风，而其他一些工程师则通过扬声器对声音的再现进行优化（电声学）；建筑师和土木工程师确保声音在音乐厅完美再现（室内声学）；听者的耳朵接收声音（生理学），听觉系统对声音进行处理，随后听者便会感知到音乐（心理声学）。

声信号从乐器传到听者耳朵的过程图解。

显而易见，声学在本质上涉及多个学科和多个物理场。在这里，我们主要讨论与工程和地球科学相关的声学物理原理。有关声学的详细分类，请参见《美国声学学会杂志》（Journal of the Acoustical Society of America） 使用的 PACS classification。

声学简史

有关声音波动性的最早推测可以追溯到亚里士多德时代，当时的古希腊哲学家已经开始了这方面的研究。他们的灵感来源于小波在水面上的传播，这些波如何与障碍物相互作用，以及振动物体如何发出声音。马兰·梅森（Marin Mersenne，1588-1648）首次提出了振弦的正确（已出版）数学描述（1636 年出版的《Harmonicorum Libri》），由于这一突出贡献，人们通常称他为声学之父。这比伽利略·伽利莱（Galileo Galilei，1564-1642）对力学的开创性研究早了两年。在梅森和伽利略时代，其他物理学家并不相信声音的波动性，有些人认为它是一种物质流（见参考资料 1、21 和 22）。

艾萨克·牛顿（Isaac Newton，1643-1727）在他的著作《自然哲学的数学原理》（Principia）（1687 年出版的第二卷）中对声音在流体中的传播提出了第一个正式的数学描述。他将声音描述为脉冲传播，其中相邻的流体质点相互作用并相互推动。牛顿基于等温假设预测了空气中的声速约为 298 m/s（979 ft/s），这一声速值和理论后来于 1816 年被皮埃尔-西蒙·拉普拉斯（Pierre-Simon Laplace，1749-1827）修正为我们现在所知的 348 m/s（1142 ft/s），这是他通过 因子（其中 表示绝热指数；请参见“流体中的线性波”一节）修正牛顿的预测得到的值。

十八世纪，随着连续介质力学和流体动力学的发展，莱昂哈德·欧拉（Leonhard Euler，1707-1783）、约瑟夫·路易斯·拉格朗日（Joseph-Louis Lagrange，1736-1813）和让·勒朗·达朗贝尔（Jean le Rond d'Alembert，1717-1783）的研究取得了进展，他们为声音的传播提出了完整的理论。大部分现代声音传播理论都建立在这些科学家及其同时代人的工作成果之上。十九世纪，拉普拉斯、克劳德-路易·纳维（Claude-Louis Navier，1785-1836）、西莫恩·德尼·泊松（Siméon Denis Poisson，1781-1840）、奥古斯特·孔特（August Kundt，1839-1894）、赫尔曼·冯·亥姆霍兹（Hermann von Helmholtz，1821-1894）和乔治·斯托克斯（George Stokes，1819-1903）的研究成果推动这一理论继续向前发展。瑞利勋爵（Lord Rayleigh，1842-1919）于 1877 年发表的专著《声学理论》（The Theory of Sound）被认为是这一漫长研究工作（对散射的详细描述等）的完结篇，这一著作常常被认为标志着经典声学到现代声学的转变（参考资料 21-22）。

控制方程的详细推导

为了推导所有波动现象的控制方程，您需要从最一般形式的守恒方程开始，即质量守恒、动量守恒和能量守恒。为了封闭方程组，需要为这些方程补充本构关系和热力学状态方程。

根据波的传播介质以及波与波之间的相互作用，存在许多不同类型的波。在下面的章节中，我们将推导流体（液体和气体）中波的控制方程，包括损耗模型和各种假设的详细信息。在此基础上，我们将给出固体中弹性波的控制方程，以及弹性波和压力波在多孔材料中进行组合传播的控制方程。

守恒方程

描述流体运动的守恒方程包括连续性方程（质量守恒）、纳维-斯托克斯方程（动量守恒）和一般传热方程（能量守恒）。这些方程给出如下

其中，自变量为时间 （SI 单位：s）和空间坐标 （SI 单位：m）。因变量为密度 （SI 单位：kg/m3）；速度场 （SI 单位：m/s）和熵 （SI 单位：J/kg/K），即单位质量的熵。此外， 为温度（SI 单位：K）， 为黏性耗散函数（W/m3）， 为总应力张量（SI 单位：N/m2）， 为黏性应力张量（SI 单位：N/m2）， 为局部热通量（SI 单位：W/m2）， 表示可能的质量源项（SI 单位：kg/m3）， 表示可能的热源（SI 单位：W/m3）， 是可能的体积力源项（SI 单位：N/m3）。这里的守恒量是密度 、动量 和总熵 。

原则上，我们将考虑质量守恒情况，因此，一般情况下 。不过，我们可以使用质量源项的声学扰动（见下文）来表示我们不想详细描述的复杂过程。

编写守恒方程和选择因变量的方法有很多，以上只是其中一种。您可以参见参考资料 1-10 或任何关于流体力学和连续物理学的教科书，获取更多信息。

方程左边的项表示守恒量，这些项有时（经操作后）也以非守恒形式写为

运算符称为材料导数，定义为

热力学关系

根据温度和压力变量重构能量守恒方程时需要一些热力学关系。这种关系的推导有多种方法，这里我们介绍其中一种。首先，我们将（等压）热膨胀系数 （SI 单位：1/K）、等温压缩系数 （SI 单位：1/Pa）以及等容比热容（单位质量热容）（SI 单位：J/kg/K）和恒压比热容 （SI 单位：J/kg/K）定义如下

请勿将恒压热容 和等容热容 分别与等熵声速变量 和等温声速变量 进行混淆。我们假设 且 ，建立密度和熵的微分式

(7)

我们可以使用 （量）定义的微分量写出上述方程的一般形式，此时还需要一个麦克斯韦关系式，给出如下

为了能够用温度和压力变量重构能量守恒方程，我们结合使用上面的麦克斯韦关系式以及 和 的定义，将熵的微分最终表示为

本构关系

本构关系是一种表达式，用于定义材料属性以及材料对外部刺激的反应或作近似处理。本构方程分别是状态方程（此处为压力和温度表示的密度），黏性应力张量 的斯托克斯表达式和傅里叶热传导定律。

其中， 为导热系数（SI 单位：W/m/K）， 为动力黏度（SI 单位：Pa s）， 为本体黏度（SI 单位：Pa s）。

本体黏度项模拟压缩和膨胀黏度效应，这两个效应实际上描述机械压力与热力学压力之间的差异，它们并不总是处于平衡状态。

此外，一般来说，所有材料属性可能都与温度和压力相关。这意味着，我们应该将材料属性看作与空间相关的量。

流体控制方程

通过对上述表达式进行多次变换，我们可以得到完整的各向同性、可压缩、黏性及热传导流体的耦合运动方程。此处使用压力 、速度 和温度 的因变量来表示。

(8)

这些方程中保留了一个非零质量源项 ，从而使动量方程和能量方程右边分别存在 和 非标准项。在几乎所有的应用中，由于质量守恒得到 ，因此都不包含这些项。

微扰理论、线性化和阶次

声学研究的是微扰的传输和传播。这些微扰可以比背景条件小多个数量级；例如，大气压约为 100,000 Pa，而正常语音信号的振幅则为 。通常情况下，求解上述完整的控制方程是不切实际的。这些方程本质上是非线性的，不仅如此，通过对比以下各项可知，它们在空间和时间上也是多尺度的：

  • 空间坐标 和波长
  • 时间 和波动周期
  • 速度场 和声速

在数值应用中，同时解析不同的物理尺度和时间尺度需要非常高的数值精度。

在大部分实际情况下，我们可以将声学问题化为线性问题，利用微扰理论，在脱离背景属性的情况下对声学进行简化分析。根据微扰展开的阶次、所模拟物理机制方程中保留项的阶数以及其他近似方法，对控制方程进行重新表述将得到不同的声学方程。这些方程可以描述从一般线性声学和亥姆霍兹方程到有关冲击的高级非线性声学模型和方程的一切过程。有关微扰理论的详细信息，请参见参考资料 1-5 和 11。

在微扰理论中，因变量 （压力、温度、速度或密度）可以展开为

其中 是一个小参数。

在大多数声学应用中，因变量都将展开为一阶，从而得到

其中去掉了 。

通常，背景场（零阶）只依赖于空间，或者与声学时间尺度相比，最多只能在时间上缓慢变化。在声流分析等特定应用中，将微扰展开到二阶以分离时间尺度（例如，见参考资料 26）。在许多教科书中，声压扰动用 表示。此处的 用来明确说明这是一阶微扰。

在线性声学中，微扰展开到一阶，控制方程中只保留一阶项（如下所示）。使用泰勒级数将状态方程中与零阶解相关的因变量展开为一阶。例如，在等熵情况（）下，可以得到

在大多数非线性声学（忽略边界层效应时）中，我们将因变量扰动展开到一阶，但控制方程中最多保留到二阶项（请参见下面的非线性声学一节）。在这种情况下，我们使用泰勒级数将状态方程展开到二阶（例如，见参考资料 25）。微扰方法不仅仅依赖于数学方案，而且在很大程度上与需要由控制方程捕获的物理效应有关。

流体中的线性波

在线性理论中，我们将控制方程线性化，并将稳态背景解附近小幅变化的参数展开为一阶形式，这种小参数变量（一阶）表示基于稳态背景平均流（零阶解）的声学变化。根据方程（8），我们可以将因变量定义为

在频域中，时间相关性为谐波形式，因变量和源可以用它们的傅里叶分量来表示。例如，压力可以表示为

通过使用一阶泰勒展开（或者通常使用上面给出的密度微分），将密度的扰动分解为压力和温度项。

我们需要理解的是，计算是在线性化点 上进行的。

这两个热力学量就是前面介绍的等温压缩系数 和（等压）热膨胀系数 ，它们与声速（行波速度）有重要的关系

(9)

其中， 是等温体积模量， 是等熵压缩系数。 量为比热率（SI 单位：1）

(10)

其中，我们已经明确指出，声速 为等熵声速，是通常给出的表称值，称为声速。等温声速由 给出。

完整的线性方程

将上述方程插入控制方程中，仅保留扰动量中的线性项，即可得到完整的线性纳维-斯托克斯方程。将这些项重排得到

(11) 其中 是黏性耗散函数。

回想一下我们前面提到的，假设背景场为稳态，或者与扰动相比，至少在时间上变化缓慢。不仅如此，一般情况下，我们假设 （由于流量总质量守恒）且 （对系统使用零熵参考）。不过，我们保留了扰动质量源项 。我们很少包含这一项，但可以用它来对不希望详细描述的复杂过程进行建模。比如，在声学中，脉动球或热注入作用可以用这种质量源项进行很好的近似。当使用二阶微扰方法时，也会出现类质量源项。

在频域中，我们将所有的时间导数 都替换为与 的乘积。在上面给出的方程中，没有对黏度或导热系数等材料属性进行扰动。在无损情况下，上述方程可以降阶为线性欧拉方程。线性欧拉方程和线性纳维-斯托克斯方程构成了气动声学领域的基础。当存在背景流 时，这些方程仍可以描述熵波和涡波等非声波的传播，它们是在背景流速的对流，对这些方程进行数值求解是一项巨大的挑战。

线性热黏性方程

在假定背景流为零 的静止情况下，完整线性方程可以简化为

(12)

这些方程明确地描述包含热损耗和黏滞损耗的声波传播，是热黏性声学方程，相关问题也称为热黏性声学。在模拟和研究微型声学器件（如移动设备和麦克风）时，为了正确预测器件的特性和响应，必须包含由热黏性方程描述的物理量。

一般线性标量波动方程和亥姆霍兹方程

如果假设系统中的热力学过程绝热可逆（等熵），并且黏度和导热系数可以忽略不计，则热黏性声学方程可以简化为

上述能量方程用来表示压力关于密度的时间微分。使用方程（7） 的密度微分、方程（10） 和（9） 中的关系式，经变换后可以得到

其中，由于假设背景场的所有时间导数均为零且 ，因此我们使用零阶动量方程来表示 。

一般情况下，当密度 不是常数时，必须使用此方程。对于材料数据为常数并且无热源的情况，该方程可以退化为普通形式 。

这个方程组构成了推导[压力声学](Summary of Acoustics Pillar#pressure_acoustics)方程的基础，其中的数学问题得到简化，只需求解包含一个因变量（压力）的方程。请注意，类似的公式也可以用速度势或密度来表示。现在，我们可以重新表述标量波动方程。利用对连续性求时间导数以及对动量方程求散度的常用技巧，并结合压力的时间导数，可以得到

(13)

这是标量波动方程的最一般形式，其源项适用于密度和声速均非恒定的情况。在频域中，通过将时间导数替换成与 的乘积，可以重新表述亥姆霍兹方程，从而得到

(14)

其中，波数为 。

在材料数据与深度相关的水声学等领域，这种控制方程的一般形式至关重要。在多物理场环境中，消声器系统中的温度分布 就是这样一个例子，它会影响材料属性， 和 。这种情况下，使用正确的公式同样非常重要。

阻抗

阻抗的概念在机械工程和声学中尤其重要，它是一个频域概念，定义为边界或点上的力与流动变量之比。阻抗边界条件可用于在不显式建模的情况下施加边界属性。因此，该边界条件概括了声硬和声软边界条件，可用于分析许多介于这两个极端之间的情况。与频率相关的阻抗可用于模拟或简化复杂的机械系统或吸收边界的属性。人体耳膜（鼓膜）的阻抗便是其中一个例子，我们可以对这种阻抗进行详细的描述和研究。

人耳鼓膜示意图，可以用阻抗条件进行描述。 鼓膜的机械属性可以通过与压力和粒子速度相关的阻抗描述进行建模和近似求解。 鼓膜的机械属性可以通过与压力和粒子速度相关的阻抗描述进行建模和近似求解。

在声学中，我们通常使用三种不同的阻抗概念：声阻抗、比阻抗和机械阻抗。声阻抗 （SI 单位：Pa*s/m3）定义为边界上的平均压力 与通过边界的体积流率 （SI 单温：m3/s）之比，

这个量有时也称为面法向阻抗 ，通常用于指定或定义边界条件。

比声阻抗 （SI 单位：Pa*s/m）定义为某个点上的压力 与粒子速度 之比

由每个点的压力与粒子速度的关系，不同的波型可以通过其各自的特性比声阻抗来定义。无损平面行波的特性（比声）阻抗由已知量 给出。最后，机械阻抗 定义为边界上的作用力 （SI 单位：N）与粒子速度之比

对于给定表面积 上具有恒定值的条件，这三个阻抗概念之间的关系如下

强度

声波的传播与能量的传递或能量的流动有关。声强大小 （或简称强度大小）定义为单位时间内通过单位面积的时间平均能量，其中面积的法向为波的传播方向。一般来说，强度是描述能量传递大小和方向的矢量 ，通过瞬时强度的时间平均值计算

其中，瞬时强度 的精确形式取决于求解的波动方程。

的表达式遵循声能推论（论述声波能量守恒；见参考资料 2 和 9），并具有不同的复杂性。积分时间 取决于声信号的类型。对于噪声来说，这是一段很长的时间，而对于谐波信号，则是信号周期。对于在无损静止流体中平面传播的波，其强度由下式给出

在更广泛的情况下，对于在频域求解的静态流体中的波动问题（求解亥姆霍兹方程），瞬时强度（强度为 ）由下式给出

其中 表示共轭复数。

在参考资料 9 中，Myers 给出了适用于所有线性声学的声能推论的非常普遍的形式。

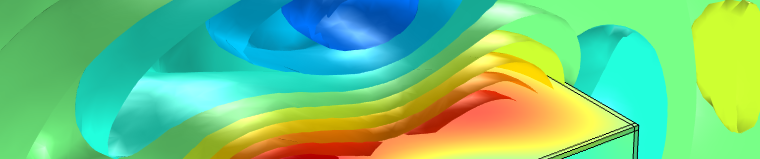
在 COMSOL Multiphysics® 中建模的吸收式消声器系统。 在 1300 Hz 下的吸收式消声器系统（使用多孔衬垫材料）示例中，使用流线描述的强度场。颜色标尺相对于入口强度来表示，单位为 dB。 在 1300 Hz 下的吸收式消声器系统（使用多孔衬垫材料）示例中，使用流线描述的强度场。颜色标尺相对于入口强度来表示，单位为 dB。

在分析能量传递和耗散时，了解系统的强度（矢量场分布）非常有用。上图显示通过吸收式消声器系统的强度。对上述消声器的入口和出口等边界上的强度进行积分，可以给出系统的总功率输入/输出。具体来说，知道边界上入射波和反射波的组合，我们可以计算传输损耗，即：发射功率与入射功率之比。对于扬声器系统，对封闭表面上法向强度的积分可以定义辐射功率。

举例来说，计算和预测人体组织或多孔材料中吸收的声能也会涉及强度。简化的半解析表达式往往需要知道强度，比如平面波吸收定律 ，其中 为耗散功率密度（SI 单位：W/m3）， 表示波数的虚部。

边界条件

在求解控制方程时，我们需要使用适当的边界条件在数学上形成封闭。这些条件描述声场如何产生，及其在边界上的特性，以及在无限域中辐射时的特性。

在没有平均背景流的情况下，声场与其周围环境相互作用的边界处会显示声学的多物理性质。在弹性结构的边界处，声场将受到结构加速度的影响，与此同时，结构也将受到压力载荷的影响。这就是典型的声振耦合或声-结构相互作用。

从数学上讲，界面上施加了两个条件：一个是表示位移（或速度）连续性的运动学条件，另一个是表示应力连续性的动力学条件。在扬声器等声源的表面，不仅会产生声音，声音还会通过附加质量影响扬声器，最后再耦合回电源。

显示轮系总成中声-结构相互作用的仿真图像。 声-结构相互作用示例，其中的声音由箱内的轮系总成发出。 声-结构相互作用示例，其中的声音由箱内的轮系总成发出。

正如前面讨论的，阻抗模型可以用作边界条件，以简化的方式对复杂系统的特性进行建模；例如，我们可以指定多孔吸收体表面的阻抗，而无需进行详细建模（参考资料 14 和 15）。在计算声学中，阻抗条件被广泛用于降低模型的复杂性。由于阻抗模型可以近似表征复杂系统的真实特性并提供简化描述，因此，我们可以将这些模型视为工程关系。在求解复杂问题时，使用阻抗条件常常可以给出比较准确的初步近似模型。

声波进入或离开系统时的特性可以用辐射条件或端口条件来描述。在数值仿真中，我们不能总是使用理想化条件，因此这类条件显得尤为重要。在波导等系统的入口处，我们应该允许波进入波导，并允许反射波离开波导。这是辐射或无反射边界条件（NRBC）的一个例子。在管道的入口和出口处，此类条件可以作为端口条件来实现。在开放系统中，波可以向无穷远处自由传播，由于波与源和散射体的距离趋于无穷，因此必须满足索末菲辐射条件。

在数值仿真中，为了避免可能影响求解精度的虚假数值反射，正确实现和表述这一条件非常重要。Bayliss、Gunzburger 和 Turkel（参考资料 23）给出了此类条件的经典示例。

一种可以替代边界条件的方法是使用泡沫材料层来模拟无限开放问题。在这样的域中，出射波在几乎没有反射的情况下被抑制。我们熟知的完美匹配层（PML）就是这样一种吸收层方法。对于实际坐标拉伸与人工数值扩散相结合的时域问题，还存在其他的表述方法。通常，我们把这些表述称为吸收层。

等效流体模型

当声波在多孔材料或狭窄管道等物体中传播时，所涉及的损耗机制可能会非常复杂，我们很难根据基本原理进行描述和建模。对于可以详细描述损耗机制的其他情况，也很难找到问题的解析解或数值解。在此类情况下，使用等效流体模型以均匀化方式描述损耗过程比较有利。这种模型的典型应用是在求解亥姆霍兹方程时，通过定义复值密度 和声速 （这两个参数通常与频率有关）来引入损耗。

我们可以使用许多等效流体模型来描述多孔材料中的损耗；例如 Delany-Bazley-Miki 模型（参考资料 14、15 和 24）和 Johnson-Champoux-Allard 模型（参考资料 14）。其原理是描述等效流-固组合系统（饱和流体和多孔基体）的频率相关有效流体密度 和有效流体的体积模量 。此类模型的有效性局限于特定的参数范围，这些范围表示刚性或柔性多孔基体近似。在数值仿真中，等效流体模型的计算要求低于求解 Biot 方程的完整多孔弹性波模型。

当声波在狭窄区域中传播时，我们需要考虑与声边界层相关的损耗（黏滞损耗和热损耗）。在大多数情况下，这需要求解完整的线性热黏性声学方程。对于窄缝或等截面波导，我们可以使用均质模型，这些模型通常称为低约化频率模型（请参见“热黏性声学”一节）。

此外，均质等效流体模型还可用于求解水声学，其中使用衰减系数 来定义损耗。计算值通常与频率有关，以奈培/米、分贝/公里或分贝/波长（参考资料 12）表示。

固体中的弹性波

当声压波与固体相互作用时，流体的压力波动在固体域上产生流体载荷，并且结构加速度作为通过流-固边界的法向加速度影响流体域。声音在固体中的传播通过固体形状和结构的小幅弹性振动来实现。

扬声器箱的振动分析示例（为便于清楚显示，变形幅度已放大）。仿真可以帮助识别那些以我们不希望的方式从扬声器系统辐射出去的振动模式。

固体中线弹性波传播的控制方程是从一般的结构力学控制方程推导出来的。我们在应力和应变小扰动的极限下对方程进行线性化处理和公式化表示。在固体材料中，应力与应变张量之间最普适的线性关系式可以写为

其中， 为柯西应力张量， 为应变张量， 为（四阶）弹性张量。

这是适用于线弹性材料的胡克定律。对于小扰动，应变张量（矢量形式）由下式给出

其中 是位移场（SI 单位：m）。

弹性波动方程由牛顿第二定律（动量守恒）得出，给定为

其中， 表示材料密度（SI 单位：kg/m3）， 和 是可能的源。

因变量和源在频域中被分解成它们的傅里叶分量，得到的固体中弹性波的类似亥姆霍兹方程由下式给出

(15)

其中 表示角频率。

多孔弹性波

多孔弹性波描述压力波和弹性波在多孔材料中的组合传播：压力波在孔隙中的饱和流体中传播，弹性波在多孔基体框架中传播。在多孔基体框架几乎静止（刚性）的极限下，我们可以使用均质等效流体模型来描述声学特性。在柔性极限下也是如此，其中框架跟随流体产生运动。不过，这种描述并不适用于所有频率或材料参数。此外，当多孔材料与振动的固体表面发生接触时，还需要包含弹性波。Biot 理论给出了一个模型，描述了求解位移 和压力 的组合传播。

使用 Biot 理论描述的平面声波的可视化效果。 使用 Biot 理论描述的平面声波撞击沉积物层的示例。波的方向用箭头显示，黑线下方为无限大的半平面。彩色部分表示空气中产生的总声场（干涉图）以及多孔材料内部产生的总声场。灰度表示多孔基体的总位移。 使用 Biot 理论描述的平面声波撞击沉积物层的示例。波的方向用箭头显示，黑线下方为无限大的半平面。彩色部分表示空气中产生的总声场（干涉图）以及多孔材料内部产生的总声场。灰度表示多孔基体的总位移。

在 Biot 于 1956 年发表的开创性著作中，他将线弹性经典理论扩展到了充满流体的饱和多孔介质中（见参考资料 16-18）。在他的理论中，体积模量和压缩系数与波频率无关，因此可以作为常数参数处理。多孔基体通过线弹性进行描述。我们可以通过考虑孔隙中饱和流体的黏度和热传导引起的频率相关损耗来引入阻尼。包含热效应的 Biot 方程的公式有时称为 Biot-Allard 理论（见参考资料 14、19 和 20）。控制方程的一种形式为

其中 是流体密度； 是流-固系统的平均密度； 是 Biot-Willis 系数（SI 单位：1），描述流体框架从刚性 到柔性 的耦合特性。在此公式中，Biot-Willis 系数假设为空间常数。

复值密度和波数定义如下

其中， 是迂曲度（SI 单位：1）或结构形式因子（高频极限）， 是孔隙率（SI 单位：1）， 是与流阻率相关的渗透率（SI 单位：m2）， 是基体的排水体积模量（真空时的体积模量）。

黏度函数 和流体压缩系数 这两个频率相关的量分别包含有关黏滞损耗和热损耗的信息。因此，我们可以将控制方程识别为具有对角应力源项（通过压力定义）的弹性波动方程（15） 和力源项（通过位移定义）的亥姆霍兹方程（14）。

数值方法和计算声学

为了使用声学控制方程（如上文“控制方程的详细推导”一节中所述）来预测换能器的特性或房间的响应等，我们需要在计算框架中对这些方程进行数值求解。这些方程只存在有限数量的解析解，这些解不适用于实际的几何、复杂边界条件或多物理场应用。求解声学控制方程的技术多种多样，但每种方法都有各自的优缺点。通常来说，不同的应用需要使用不同的方法。

在求解声学问题时，我们要做的第一个选择是，在频域还是时域求解波动方程。当然，这是一个宽泛的问题，原因是有些方法同时依赖于这两种方法。对于所有的公式，我们都需要所用的方法能同时在时域/频域和空间中解析波，同时还需要考虑频率组成、波长、几何细节、可能的声学边界层等各种因素。

由此，我们可以使用以下多种方法中的一种来求解方程：

  • 有限元法（FEM）
  • 积分法，如边界元法（BEM）
  • 间断伽辽金（DG）法
  • 高频方法，如射线追踪和波束追踪
  • 时域有限差分（FDTD）
  • 基于波的方法
  • 有限体积法
  • 波数积分技术
  • 固有模态
  • 抛物线方程法

请注意，在气动声学领域，有一个专门的学科叫做“计算气动声学”（CAA），用于求解气流与声学之间的相互作用。

声学分析类型

压力声学

在压力声学中，只使用一个因变量来表示声场：压力。在时域求解标量波动方程（13），并在频域求解亥姆霍兹方程（14）。从某种意义上说，这就是经典声学。

对于许多情况下的声学，我们都可以使用这两个方程进行描述，比如，散射和辐射问题、消声器系统、汽车车厢声学，等等。这两个方程的一般形式可用于模拟具有非恒定密度和声速的问题，例如分析水声学或具有背景温度分布的多物理场问题。

我们可以在各种边界条件下求解这两个方程。在频域中，使用等效流体模型（均质）能够以简化的方式在多孔介质和窄波导中添加复杂的损耗效应。阻抗边界条件可以用来模拟与复杂环境的相互作用。

声学和多物理场

声-结构相互作用

有关固体中的弹性波与流体中的压力波相互作用的多物理场分析称为声-结构相互作用或振动声学。这是声学中一种特殊形式的流-固耦合（FSI）。

在大多数实际应用中，声音由振动表面产生或通过结构进行传递，因此声-结构相互作用非常重要。这些应用包括消声器、扬声器、隔音问题和机器声学的设计和优化。

多孔弹性波

在多孔材料中，为了分析多孔基体中的弹性波与饱和孔隙流体中的压力波的耦合传播，需要求解 Biot 方程，其中包含孔隙流体对组合波传播的阻尼作用。

多孔弹性应用的例子包括弹性波在岩石、土壤和沉积物中的传播，以及微粒过滤器、消声器和车厢多孔衬里的声衰减属性建模。

压电声学

压电声学是一种多物理现象，用于解释如何通过压电材料产生和检测声信号。压电换能器是压电声学最重要的应用领域，例如，水下声呐应用中需要使用此类换能器。

管道中的声波

在管道系统中，声波的传播具有主导方向，此时可以简化数学描述。我们可以对管道横截面的影响进行积分，将三维问题简化为一维方程组，从而可以对大型管道系统进行显著简化的数值处理。不仅如此，还可以通过修改流体的有效压缩系数来包含管道弹性壁的影响。

电声学

电声学主要研究如何通过机电声换能器产生和检测声信号，包括扬声器、耳机、麦克风和 MEMS 换能器；近年来，移动设备中音频组件的建模和设计（在很大程度上）都属于这一范畴。

对这些设备的建模体现了实际的多物理场应用，其中，物理场之间的双向耦合非常重要。仿真可以包含电磁学、结构力学和声学的完整详细模型，然后通过有限元法求解模型，也可以将 FEM 与使用电路/SPICE 图的集总表示相结合进行求解。

热黏性声学

在模拟或研究移动设备、麦克风、助听器和穿孔板等微型声学器件时，为了正确预测这些器件的特性和响应，必须包含热黏性声学方程描述的物理效应，其中，与黏性声学和热声边界层相关的损耗尤为重要。

在此类应用中，决定其是否为小器件的因素不是特征几何尺寸，而是这些层的厚度。此外，热黏性声学还可以精确预测电容式麦克风等器件的小缝隙中从绝热到等温特性的过渡。

气动声学

气动声学的研究涉及背景平均流与声场之间的相互作用，包括湍流或周期性流动结构产生的声音，以及流体流动对声场的影响。

应用示例包括消声器设计，其中平均流会显著影响消声器性能；科里奥利流量计；以及喷气发动机噪音的产生和传播。

在解决气动声学问题时，我们可以求解许多控制方程公式，包括声学类比方程、线性公式，以及求解完全非线性流动问题的所有细节。部分示例如下：

  • Lighthill 声学类比方程
  • 线性纳维-斯托克斯方程
  • 线性欧拉方程
  • 线性势流方程
  • 声学扰动方程（APE）
  • 完全可压缩流动方程的直接数值仿真（DNS）

几何声学

几何声学提供求解高频极限下的声学问题的方法，此时所研究的特征波长远小于几何特征。其中包括假设声音沿着射线或管道传播的射线追踪方法，这些方法不仅用于对房间、音乐厅和车厢声学进行建模，还广泛用于水声学、室外噪声传播和声音映射等多个方面。

能量法

另一类用于求解大规模声学问题的方法称为能量法，包括统计能量分析（SEA）方法、能量有限元法（EFEM）以及其他形式的声学扩散方程。这些方法不解析声波，而仅限于声波和振动的能量传递，适用于汽车和房屋等复杂的耦合系统以及纯室内声学。

水声学

水声学主要研究声音在海洋和其他水体中的传播，包括研究与海底（海床）和海面以及与潜艇等水下物体的相互作用。由于声音在海洋中进行长距离传播，因此，衰减、声速和密度随深度的变化等影响变得非常重要。典型的应用领域包括声呐、地震勘探、水下通信和海洋生物学。

非线性声学

当声波的振幅变得足够大时，最常用的线性假设不再有效。例如，行波的波谷和波峰将不再以相同的速度运动，信号也会失真。涡度、非常大的时间尺度和尺寸差异等其他影响因素也会引起非线性现象。为了捕捉这些影响，我们需要使用非线性声学公式，或者可能需要求解完全可压缩流动方程。

在超声造影和扫描等需要高振幅的超声应用中，我们常常会遇到非线性效应。实际上，某些成像技术依靠非线性和产生二次谐波来提高分辨率。我们可以在扬声器端口和穿孔板中观察到因旋涡产生引起的非线性效应，这些位置会产生声音失真。在微流体（声流体）中，由于时间尺度差异非常大，导致非线性贡献累积，从而产生声流和辐射力等声泳效应。

发布日期：2018 年 6 月 11 日
上次修改日期：2018 年 6 月 11 日

参考资料

  1. D.T. Blackstock, Fundamentals of Physical Acoustics, John Wiley & Sons, 2000.

  2. A.D. Pierce, Acoustics, "An Introduction to Its Physical Principles and Applications," Acoustical Society of America, 1991.

  3. S. Temkin, "Elements of Acoustics," Acoustical Society of America, 2001.

  4. P.M. Morse and K.U. Ingard, Theoretical Acoustics, McGraw Hill (Princeton University Press), 1986.

  5. H. Bruus, Theoretical Microfluidics, Oxford University Press, 2010.

  6. G.K. Batchelor, An Introduction to Fluid Dynamics, Cambridge University Press, 2000.

  7. L.D. Landau and E. M. Lifshitz, Fluid Mechanics, Course of Theoretical Physics, Volume 6, Butterworth-Heinemann, 2003.

  8. B. Lautrup, Physics of Continuous Matter, Exotic and Every Day Phenomena in the Macroscopic World, 2nd ed., CRC Press, 2011.

  9. M.K. Myers, "Transport of energy by disturbances in arbitrary steady flow," J. Fluid Mech. 226, pp. 383–400, 1991.

  10. F.V. Hunt, "Notes on the Exact Equations Governing the Propagation of Sound in Fluids," J. Acoust. Am. 27, pp. 1019–1039, 1955.

  11. C.M. Bender and S.A. Orszag, Advanced Mathematical Methods for Scientists and Engineers: Asymptotic Methods and Perturbation Theory, Springer, 1999.

  12. F.B. Jensen, W.A. Kuperman, M.B. Porter, and H. Schmidt, Computational Ocean Acoustics, Springer, 2011.

  13. H. Kuttruff, Room Acoustics, CRC Press, 2009.

  14. J.F. Allard and N. Atalla, Propagation of Sound in Porous Media, Modeling Sound Absorbing Materials, 2nd Edition, John Wiley & Sons, 2009.

  15. T.J. Cox and P. D’Antonio, Acoustic Absorbers and Diffusers, Taylor and Francis, 2nd ed., 2009.

  16. M.A. Biot, “Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid. I. Low-frequency Range,” J. Acoust. Soc. Am., vol. 28, pp. 168–178, 1956.

  17. M.A. Biot, “Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid. II. Higher Frequency Range,” J. Acoust. Soc. Am., vol. 28, pp. 179–191, 1956.

  18. M.A. Biot, “Generalized Theory of Acoustic Propagation in Porous Dissipative Media,” J. Acoust. Soc. Am., vol. 34, pp. 1254–1264, 1962.

  19. J.F. Atalla, R. Panneton, and P. Debergue, "A mixed displacement-pressure formulation for poroelastic materials," J. Acoust. Soc. Am., vol. 104, pp. 1444–1452, 1998.

  20. J.F. Atalla, M.A. Hamdi, and R. Panneton, "Enhanced weak integral formulation for the mixed (u-p) poroelastic equations," J. Acoust. Soc. Am. vol. 109, pp. 3065–3068, 2001.

  21. J.W.S. Rayleigh, The Theory of Sound: Introduction by R.B. Lindsay, Dover Publications, 1945.

  22. R.B. Lindsay, "The Story of Acoustics," J. Acoust. Soc. Am., vol. 39, pp. 629–644, 1966.

  23. A. Bayliss, M. Gunzburger, and E. Turkel, “Boundary Conditions for the Numerical Solution of Elliptic Equations in Exterior Regions,” SIAM J. Appl. Math., vol. 42, no. 2, pp. 430–451, 1982.

  24. Y. Miki, “Acoustical properties of porous materials - modifications of Delany-Bazley models,” J. Acoust. Soc. Jpn (E), vol. 11, no. 1, 1990.

  25. M.F. Hamilton and D.T. Blackstock (edited by), Nonlinear Acoustics, Acoustical Society of America, 2008.

  26. P. Barkholt Muller and H. Bruus, "Numerical study of thermoviscous effects in ultrasound-induced acoustic streaming in microchannels," Phys. Rev. E 90, 043016 1–12, 2014.