带标签的博客文章 半导体模块

使用 COMSOL 模拟太赫兹光电导天线
光电导天线常用于太赫兹工程。了解这些设备的工作原理,以及如何使用半导体模块和RF模块对其进行模拟。

COMSOL Multiphysics® 能求解氢原子吗?
在这篇博客中,你将得到量子力学的介绍,并学习如何建立氢原子的模型。

使用基准模型提取比接触电阻率
现在可以使用半导体模块为金属触点增加接触电阻。在这篇博文中,我们将探索一个利用这一新功能的基准模型。

通过仿真 App 优化光电化学(PEC)太阳能水分解装置
SolCelSim 仿真 App 由 Zilina 大学的一名理学硕士生设计,使研究人员能够模拟太阳能电池设计,即使他们不熟悉仿真软件。
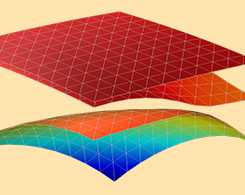
使用 COMSOL 对半导体器件材料的能带结构进行仿真
使用薛定谔方程接口中的多分量波函数功能对各种半导体系统进行建模,例如具有自旋和应变纤锌矿晶体的粒子。

玻色-爱因斯坦凝聚中的涡旋晶格形成模拟
我们讨论了漩涡晶格的形成,这是一个可以使用COMSOL Multiphysics®和半导体模块模拟的迷人过程。

在 COMSOL 中可以使用哪个模块进行电磁学模拟?
很多人经常会有这样的疑问:“我应该使用哪种 COMSOL 产品来模拟特定的电磁设备或应用?”除了 COMSOL Multiphysics® 软件基本模块的功能之外, COMSOL 产品树的“电磁模块”分支中目前还有 6 个模块。另外 6 个模块分布在其余产品分支中。
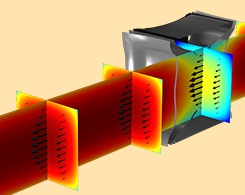
基于密度-梯度理论建立的三种半导体器件模型
你可以用密度梯度理论来模拟半导体器件。这里有三个例子:硅反转层、硅纳米线 MOSFET 和 InSb p 沟道 FET。

密度梯度理论简介——半导体器件仿真
密度梯度理论是一种有效的计算方法,将量子约束包含在模拟半导体器件的漂移扩散公式中。
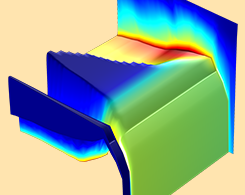
半导体器件中的辐射效应仿真
半导体中的辐射效应是一个复杂的物理现象,广泛存在于许多技术领域并产生影响,例如电子工业、医学成像、核工程以及航空航天和军事应用。基于早期的论文研究(参考文献1),本文通过一个 COMSOL 案例教程,介绍了如何在 COMSOL® 软件中研究 p-i-n 二极管(又称 PIN 二极管)对电离辐射的电子响应。
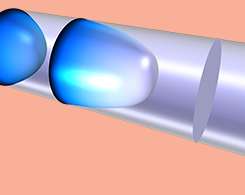
动能集合模型中的载流子热输运项
巴塞罗那自治大学(Universitat Autònoma de Barcelona, UAB)的F. Xavier Alvarez讨论了借助COMSOL Multiphysics® 在纳米尺度上模拟传热,从而更好地理解传热过程。

如何模拟半导体器件中的载流子动力学
通过 2 个示例了解如何模拟半导体器件中的载流子动力学:反向恢复和正向恢复 PIN 整流器模型。

如何模拟金属-硅-氧化物电容器的界面陷阱效应
想要分析 MOSCAP 中的界面捕获效果吗?了解如何使用半导体模块中的功能,使您能够向模型添加充电和载波捕获/释放效果。

模拟渐变异质结中的隧穿电流
对半导体设计感兴趣吗?了解量子隧穿效应背后的理论,并通过演示学习如何模拟渐变异质结中的量子隧穿电流。

纳米线基准模型的自洽薛定谔-泊松结果
使用砷化镓纳米线的基准模型验证了“薛定谔-泊松方程”多物理场接口,此接口适用于模拟包含载流子的量子约束系统。

通过多物理场仿真模拟优化 ISFET 设计
你知道啤酒发酵、土壤分析和乳制品生产有什么共同点吗?它们都涉及使用离子敏感场效应晶体管(ion-sensitive field-effect transistors,ISFETs)来测量酸碱度。这类传感器体积小、效率高、耐用,因此适用于食品、环境和生物医学应用。

使用半导体模块模拟 MOS 电容器
MOS 电容(MOSCAP)主要由三个部分构成:半导体主体或衬底、绝缘膜和金属电极(或栅极)。您可以使用“半导体模块”来模拟 MOS 电容设计。
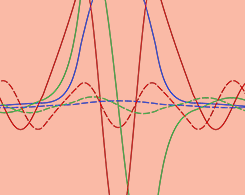
学习双势垒结构的量子力学概念
众所周知,量子力学是一门难以学习和教授的学科。 对双势垒结构建模是向物理学学生教授量子力学概念的有效方法。
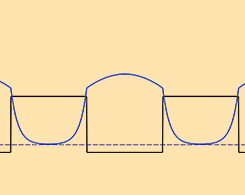
使用薛定谔方程计算超晶格的带隙
在最新版本的 COMSOL® 软件中,您可以在半导体模块中使用新的薛定谔方程 接口进行建模。今天这篇博文,让我们来看一个简单的示例模型,这个模型使用了此接口来估计超晶格结构的电子和空穴基态能级。通过构建类似的模型,器件工程师能够计算给定周期结构的带隙并调整设计参数,直到达到所需的带隙值。 编者注:此博文于 2020 年 1 月 23 日更新,反映了软件最新的功能和信息。 超晶格结构的有效带隙 由于量子限制效应,超晶格结构的有效带隙比体阱材料中的有效带隙更宽——电子和空穴大多被限制在阱中,其基态能量从带边缘偏移。下面显示了一个示例,其中黑色和灰色线表示导带和价带边缘,蓝色和绿色曲线分别表示电子和空穴波函数被基态能量偏移。 超晶格带隙模型的汇总图。 COMSOL Multiphysics® 模型 这个模型简单明了,易于理解。使用了两个 薛定谔方程 接口:一个用于电子,另一个用于空穴。在每个接口下,两个 电子势能 节点用于设置方波形带边缘,同样,两个 有效质量 节点用于设置阱区和势垒区的有效质量。模型中只需要包含一个超晶格结构的晶胞,端点应用 周期性条件 边界条件。 COMSOL 模型开发器树结构。 在两个特征值研究中分别求解电子和空穴的基态能量。使用 数组 一维数据集将结果从一个晶胞扩展到三个晶胞 ,这也是 COMSOL Multiphysics® 软件的新增功能。 关于 薛定谔方程 接口 在物理场接口的设置面板中有一些参数值得注意。 薛定谔方程接口的设置面板。 特征值尺度 一个重要的参数是特征值尺度 λscale (单位: J)。这个参数用于特征值研究,将无单位的特征值相对于特征能量进行缩放。例如,默认值 1eV 允许特征值的数值以 eV 为单位呈现特征能量的值。因此,1.924 的特征值(如下面的屏幕截图所示)对应于 1.924eV 的特征能量。 特征值研究的设置。 如果将特征值比例设置为 1meV,那么相同的特征值将对应于 1.924 meV 的特征能量(来自不同模型的结果)。 能量 另一个参数是能量E(单位:J),用于稳态研究以指定稳态薛定谔方程的总能量。 薛定谔方程接口中的符号约定 时谐因子 在物理场接口中执行的单分量薛定谔方程如下: -\hbar^2 \nabla \cdot \left(\frac{\nabla \Psi(\mathbf {r},t)}{2\, m_{eff}(\mathbf{r})}\right) + V(\mathbf{r},t)\Psi(\mathbf{r},t) = -i \hbar \frac{\partial}{\partial t}\Psi(\mathbf{r},t) 请注意,方程右侧的能量算子采用了与大多数量子力学教科书采用的符号相反的约定。这是因为 COMSOL Multiphysics 对时谐解采用了exp(+iωt) 的工程惯例来约定 ,而不是 exp(–iωt) 的物理学约定。薛定谔方程 接口采用工程约定,因此 COMSOL® 系列产品中的符号约定保持一致。在这种不寻常的符号约定下,动量算子也获得了相反的符号——因为平面波现在是 exp(–ikx + iωt),而不是 exp(+ikx – […]

如何对半导体器件执行三维仿真分析
在改进半导体器件研发流程和制造技术的过程中,仿真具有巨大的应用潜力。通过仿真分析可以减少设计过程中所需的试验和制造次数。由于必须解决器件的长度尺度问题,以及半导体物理现象的非线性特性,对三维半导体器件进行建模具有一定的挑战性,往往需要进行计算量非常大的仿真工作。
