在 COMSOL 中可以使用哪个模块进行电磁学模拟？

很多人经常会有这样的疑问：“我应该使用哪种 COMSOL 产品来模拟特定的电磁设备或应用？”除了 COMSOL Multiphysics^® 软件基本模块的功能之外， COMSOL 产品树的“电磁模块”分支中目前还有 6 个模块。另外 6 个模块分布在其余产品分支中。这些模块代表了麦克斯韦方程组与其他物理场耦合的各种形式。今天这篇博文，我们将带您看一看它们都有什么功能。

注意：此博客最初发布于 2013 年 9 月 10 日。此后更新了一些信息和示例。

计算电磁学：麦克斯韦方程组

麦克斯韦（Maxwell）方程组与电荷密度 \rho、电场 \mathbf{E}、电位移场 \mathbf{D}、电流 \mathbf{J}、磁场强度 \mathbf{H}，以及磁通密度 \mathbf{B} 有关：

 
为了求解这些方程，我们需要一组边界条件，以及材料本构关系。本构关系将 \mathbf{E} 和 \mathbf{D}场、 \mathbf{J} 和 \mathbf{E} 场、\mathbf{B} 和 \mathbf{H} 场相关联。在不同的假设下，这些方程已在 COMSOL 产品库的不同模块中被求解，并与其他物理场耦合。

注意：为了传达关键理念，此处介绍的大多数方程均以缩写形式显示。要查看所有控制方程的完整形式，并查看所有可用的本构关系，请查阅产品文档。

下面，我们先开始介绍一些概念。

稳态、时域还是频域？

在求解麦克斯韦方程组时，为了减轻计算负担，我们试图做出尽可能合理和正确的假设。尽管麦克斯韦方程组可以求解任意随时间变化的输入，但我们通常可以合理地假设输入和计算的解都是稳态或正弦时变的情况。前者通常也被称为 DC（直流）情况，而后者通常被称为 AC（交流）或频域情况。

如果这些场在任何时间都没有变化，或者变化很小以至于不重要，则稳态（DC）假设成立。也就是说，我们可以说麦克斯韦方程组中的时间导数项为零。例如，如果您的设备连接了电池（可能需要数小时或更长时间才能耗尽电量），那么这样做是非常合理的假设。更正式地，我们可以这样说：\frac{\partial \mathbf{B}}{\partial t} = \frac{\partial \mathbf{D} }{\partial t} = 0 ，它直接就忽略了麦克斯韦方程组中的两个项。

如果系统上的激励呈正弦变化，并且系统的响应在相同频率下也呈正弦变化，则频域假设成立。换句话说，系统的响应是线性的。在这种情况下，我们可以使用以下关系式在频域中，而不是在时域中求解问题：\mathbf{E}(\mathbf{x},t) = \Re \left( \exp ^{j \omega t }\mathbf{E_c}(\mathbf{x}) \right)，其中 \mathbf{E}(\mathbf{x},t) 是时空变化场； \mathbf{E_c}(\mathbf{x}) 是一个空间变化的复值场；\omega 是角频率。与时域相比，在一组离散频率中求解麦克斯韦方程组的计算效率非常高，尽管计算要求与要求解的不同频率的数量成正比（我们将在后面讨论一些注意事项）。

当解随时间变化或系统响应为非线性时，就需要在时域内求解（尽管对此有一定的例外，我们将在后面讨论）。时域仿真比稳态或频域仿真在计算上更具挑战性，因为其求解时间与感兴趣的时间跨度和所考虑的非线性因素成比例增加。在时域内求解时，最好考虑输入信号的频率组成，尤其是当前存在且重要的最高频率。

电场、磁场或两者兼有？

尽管我们可以使用麦克斯韦方程组求解电场和磁场，但通常只需求解一个就足够了，尤其是在直流情况下。例如，如果电流很小，则磁场将会很小。即使在电流较高的情况下，我们实际上也可能不会对所产生的磁场感到担忧。另一方面，有时仅存在磁场，而没有电场，例如仅由磁体和磁性材料组成的设备。

但是，在时域和频域中，我们必须更加小心。我们要在此处检查的第一个量是模型中材料的集肤深度。金属材料的集肤深度通常约为 \delta = \sqrt{2/{\omega \mu \sigma} }，其中 \mu 是磁导率，\sigma 是电导率。如果集肤深度远大于 物体的特征尺寸，则可以合理地认为集肤深度效应可忽略不计，并且只需求解电场。但是，如果集肤深度等于或小于物体的大小，则感应效应很重要，并且我们需要同时考虑电场和磁场。在开始任何模拟之前，最好快速检查一下集肤深度。

随着激励频率的增加，了解设备的一阶共振也很重要。在基本共振频率下，电场和磁场中的能量恰好处于平衡状态，因此我们可以说处于高频 状态。尽管共振频率通常很难估计，但是比较特征物体的尺寸 L_c 和波长 \lambda = c/f 是一个良好的经验法则。如果物体尺寸接近波长的重要部分 L_c \approx \lambda/100，则我们正在接近高频状态。在这种状态下，功率主要通过电介质中的辐射流动，而不是通过导电材料中的电流流动。这导致控制方程的形式略有不同，明显低于一阶共振频率，通常称为低频 状态。

现在让我们看看这些不同的假设是如何被应用于麦克斯韦方程组，并为我们提供不同的方程组来求解，然后看看我们需要为每个方程组使用哪些模块。

稳态电场模拟

在稳态条件下，我们可以进一步假设我们仅在处理导电材料或完全绝缘的材料。在前一种情况下，我们可以假设电流在所有域中流动，并且麦克斯韦方程组可以重写为：

这个方程求解了电势场 V，并能得出电场 \mathbf{E} = -\nabla V 以及电流 \mathbf{J} = \sigma \mathbf{E}。我们可以使用 COMSOL Multiphysics 基本模块求解该方程，并在软件的 入门简介中求解。AC/DC 模块和MEMS 模块扩展了基本模块的功能，例如，通过提供简化模型设置的终端条件和用于模拟相对较薄的导电和绝缘区域的边界条件，以及模拟仅通过几何上较薄并可能具有多层结构的电流的单独物理场接口。

另一方面，假设我们对材料介电常数为 \epsilon 的完全绝缘介质中的电场感兴趣，可以求解方程：

 
该方程计算了不同电势下对象之间的介电区域中的电场强度。该方程也可以使用 COMSOL Multiphysics 基本模块求解，并且 AC/DC 和 MEMS 模块再次通过例如终端条件、模拟薄介电区域的边界条件和介电材料中的薄间隙扩展了功能。此外，这两种产品还提供了边界元公式，它求解了相同的控制方程。如之前的博客文章所述，它对于仅由导线和表面组成的模型也具有一些优势。

时域和频域电场模拟

一旦要模拟时变电场，就会同时存在传导电流和位移电流，这时我们会想使用 AC/DC 模块或 MEMS 模块。与上面的第一个方程略有不同，在时域情况下，求解方程可写为：

这个瞬态方程可以同时求解传导电流，\mathbf{J}_c = \sigma \mathbf{E} 和位移电流 \mathbf{J}_d = \frac{ \partial \mathbf{D}
}{\partial t}。当源信号不是谐波，并且我们希望随时间监视系统响应时，可以使用此方法。电路中电容器的瞬态模拟模型是一个你可以查阅的示例。

在频域中，我们可以求解稳态方程：

 
此时，位移电流为 \mathbf{J}_d = j \omega \epsilon \mathbf{E}。使用此方程的一个示例是电容器频域模拟。

使用 AC/DC 模块模拟磁场

AC/DC 模块解决了稳态、时域或低频状态下的磁场模拟问题。

对于没有电流流过的模型（例如磁体和磁性材料的模型），可以简化麦克斯韦方程组并求解磁标势 V_m ：

 
可以使用有限元法或边界元法求解该方程。

一旦模型中存在稳态电流，我们就必须求解磁矢势 \mathbf{A}。

 
该磁矢势用于计算 \mathbf{B} = \nabla \times \mathbf{A}，并且电流 \mathbf{J} 可以通过施加或通过增广先前的电标势和电流方程来同时计算。这种情况的典型例子是亥姆霍兹线圈的磁场。

当移至时域时，我们求解以下方程式：

 
其中， \mathbf{E} = -\frac{ \partial \mathbf{A}}{\partial t} 。

该方程式仅考虑传导电流和感应电流，而不考虑位移电流。如果功率传输主要是通过传导而不是辐射进行，这就是合理的。求解此方程式的一个重要动机是，是否存在材料非线性，例如，E 型磁芯变压器这个示例的 BH 非线性材料。但是，应该指出的是，还有通过等效 HB 曲线方法求解 BH 非线性材料的替代方法。

当我们进入频域时，控制方程变为：

 
请注意，该方程式同时考虑了传导电流 \mathbf{J}_c = -j \omega \sigma \mathbf{A}，以及位移电流 \mathbf{J}_d = \omega^2 \epsilon \mathbf{A}，并且开始看起来非常类似于波动方程。实际上，在假设辐射可忽略不计的情况下，该方程可解决结构谐振及其周围频率的问题，如这个示例所示：三维电感器模拟。

有关上述方程组在磁场模拟中的用法的更完整介绍，请参阅我们关于电磁线圈建模的系列讲座。

也可以将磁标势方程式和矢势方程式混合，这在电动机和发电机模拟中都有应用。

除了上述关于磁矢势和标势的静态、瞬态和频域方程式之外，还存在关于磁场的单独公式，适用于超导材料的模拟，例如以下所示的超导线示例。

使用 RF 模块或波动光学模块模拟频域和时域中的波动方程

当我们进入高频状态时，电磁场在本质上会体现波动性，就像 天线、微波电路、光波导、微波加热、自由空间中的散射和基底上对象的散射模拟一样，我们在频域中求解形式与麦克斯韦方程组稍有不同：

 
这个方程是用电场 \mathbf{E} 来写的，并且磁场的计算公式为：j \omega \mathbf{B} = \nabla \times \mathbf{E}  。它既可以以一组指定的频率来求解，也可以作为特征频率问题来求解，它可以直接求解设备的谐振频率。特征频率分析的示例包括闭合腔、线圈和法布里-珀罗腔多个基准示例,，并且此类模型可以计算谐振频率和品质因子。

在指定频率范围内求解系统响应时，可以直接在一组离散频率上求解，在这种情况下，计算成本与指定频率的数量成线性比例关系。人们也可以在单台计算机和集群上利用硬件并行来并行化和加速求解。也有频域模态和自适应频率扫描（也称为渐近波形估计）求解器，这些求解器可加速求解某些类型的问题，如本博文中的一般意义所述，并在此波导虹膜滤波器示例中进行了演示。

如果您要使用 RF 模块或波动光学模块在时域中求解，那么我们可以求解与 AC/DC 模块中较早的方程非常相似的方程：

 
该方程式再次求解了磁矢势，但是在时间上包括一阶和二阶导数，因此同时考虑了传导电流和位移电流。它可用于光学非线性，色散材料和信号传播的模拟。如本示例所示，时域结果还可以通过快速傅立叶变换求解器转换为频域。

这些等式在存储方面的计算要求也是一个问题。感兴趣的设备及其周围的空间通过有限元网格离散化，并且该网格必须足够精细以解析波。也就是说，至少必须满足奈奎斯特准则。实际上，这意味着大约 10x10x10 波长的域大小（不考虑工作频率）大约是 64GB RAM 的台式计算机上可寻址内容的上限。随着域大小的增加（或频率增加），内存需求将与要求解的立方波长的数量成比例地增长。这意味着上述方程式非常适合于特征尺寸大约不大于感兴趣的最高工作频率下 10 倍波长的结构。但是，有两种方法可以绕过此限制。

求解远远小于波长的对象周围的类波场的一种方法是时域显式方程。这求解了另一种形式的与时间相关的，且可以使用更少的内存来求解的麦克斯韦方程。它主要用于线性材料模拟，在某些情况下很有吸引力，例如用于计算背景场中对象的宽频带散射。

对于特定类型的光波导结构，存在另一种替代方法，可以在已知电场在传播方向上的变化非常缓慢的频域中求解。在这种情况下， 波动光学模块中的波束包络法变得非常有吸引力。此接口求解以下方程：

 
其中，电场为 \mathbf{E} = \mathbf{E_e} \exp \left (-i \phi \right)，\mathbf{E_e} 是电场包络。

附加场 \phi 是所谓的必须已知的相函数，并将其指定为输入。幸运的是，对于许多光波导问题，确实是这种情况。可以同时求解一个或两个这样的波束包络场。当可以使用这种方法时，其优点是内存要求远远低于本节开头介绍的全波方程式。其用法的其他示例包括定向耦合器模型以及光学玻璃中的自聚焦模型。

在 AC/DC 模块、RF 模块和波动光学模块之间选择

AC/DC 模块和 RF 模块之间的分界线有点模糊。问我们自己几个问题会有所帮助：

1. 我正在使用的设备会辐射大量能量吗？我对计算谐振感兴趣吗？如果是这样，则RF模块更合适。
2. 设备是否比最高工作波长的波长小得多？我主要对磁场感兴趣吗？如果是这样，则 AC/DC 模块更合适。

如果您正好介于两者之间，那么将这两种产品都包含在模块库中是合理的。

在 RF 模块和波动光学模块之间选择需要询问您自己的应用。尽管在时域和频域上，麦克斯韦方程组的全波形式在功能上存在许多重叠，但在边界条件上仍存在一些细微差异。存在适用于微波设备模拟的所谓集总端口和集总元件边界条件，它们只包含在 RF 模块中。还请记住，只有“波动光学模块”包含波束包络公式。

就材料特性而言，这两种产品具有不同的材料库：RF 模块提供了一套通用的电介质基底，而波动光学模块则在光学和红外频带中包含了上千种不同材料的折射率。有关此内容以及其他可用材料库的更多详细信息，请参见此博客文章。当然，如果您对设备模拟需求有特定疑问，请与我们联系。

下图概述了这些模块之间的近似分界线。

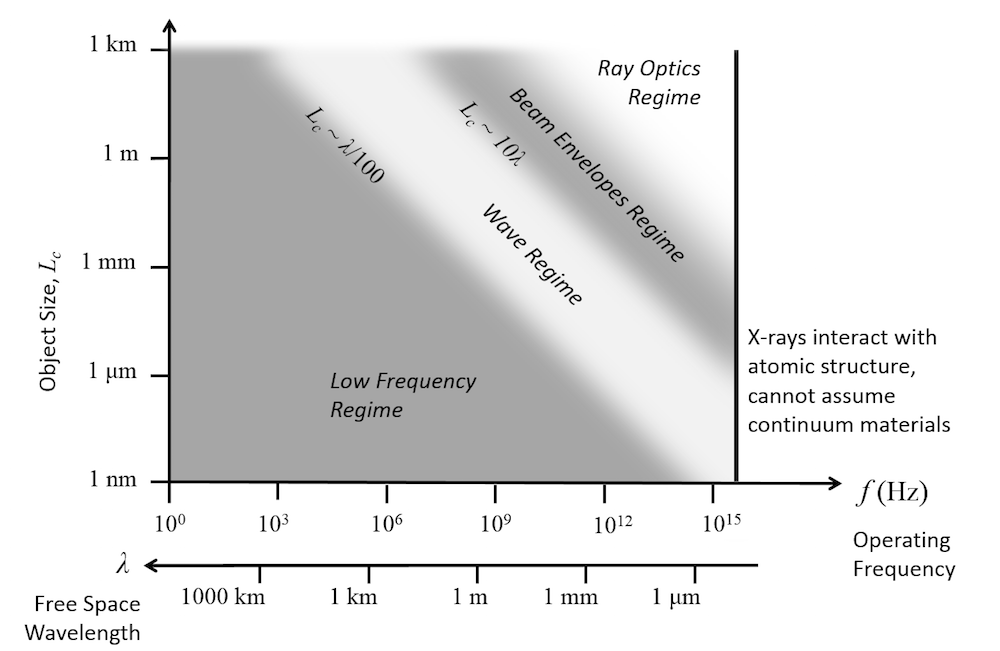
使用射线光学模块追踪射线

如果要模拟大小是波长数千倍的设备，则不再可能通过有限元网格来解析波长。在这种情况下，我们还在射线光学模块中提供了几何光学方法。这种方法不直接求解麦克斯韦方程组，而是模拟空间追踪光线。这种方法仅需要将反射表面和介电区域进行网格剖分，而不是均匀的自由空间。它适用于透镜、望远镜、大型激光腔以及结构-热-光学性能（STOP）分析的模拟。甚至可以将其与全波分析的输出结合起来，如本示例所示的教程模型。

多物理场模拟

除了求解麦克斯韦方程组本身之外，COMSOL Multiphysics 的核心优势之一是求解几个物理场之间存在耦合的问题。最常见的方法之一是麦克斯韦方程组和温度之间的耦合，其中温度的升高会影响电（以及热）的特性。有关解决此类电热问题的方法概述，参见此博客文章。

将结构变形与电场和磁场耦合也是很常见的。有时，这仅涉及变形，但有时，还涉及压电、压阻或磁致伸缩材料响应，甚至应力-光学响应。MEMS模块具有用于静电驱动谐振器的专用的用户接口，其中施加的电场使设备偏置。结构接触和接触部分之间的电流流动也可以在电流模拟的背景下考虑。

但是，除了温度和变形之外，您还可以将麦克斯韦方程组的电流耦合到化学过程，如电化学，电池和燃料电池，电沉积和腐蚀模块所述。在“等离子体模块”中，您甚至可以耦合到等离子体化学，并且通过“粒子追踪模块”，您可以通过电场和磁场追踪带电粒子。最后，我们的半导体模块使用漂移扩散方程求解电荷传输。这些模块中的每个模块本身都是一个主题，因此我们不会在这里详述。

当然，如果您想更深入地讨论这些模块中的任何一个，并了解它如何适用于您感兴趣的设备，请立即通过下面的按钮与我们联系。