由 Nancy Bannach 创作的所有博客

模拟狭窄肺动脉中的血液流动
2025年 6月 11日
狭窄的肺动脉中的血流可以通过将狭窄部位视为多孔介质进行模拟。点击此处了解更多。

非牛顿流体在多孔介质中的流动仿真
2025年 3月 27日
学习如何使用仿真开发一种均质化方法,用于模拟多孔结构中的非牛顿流。

使用 COMSOL 模拟蒸发冷却效应
2022年 2月 22日
从气象学到食品加工,蒸发具有许多工业和科学应用。 在这里,我们将介绍如何使用传热模块模拟蒸发。
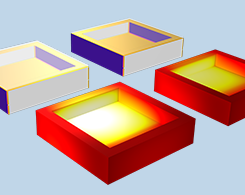
应该使用哪个辐射接口建立传热模型?
2021年 3月 4日
与传导和对流传热机制相比,辐射传热有其独特的特点。例如,辐射不需要任何介质就能远距离传输热量,在非常高的温度下主要是辐射传热产生作用。此外,辐射依赖于方向、波长和温度。那么,在 COMSOL Multiphysics 软件中,哪个接口可以最好地考虑我们传热模型中的辐射?
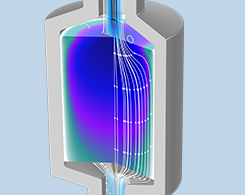
多孔介质中的热平衡与热非平衡传热
2020年 3月 3日
多孔材料的应用越来越广泛,因为它适用性强、成本低,具有特殊的热特性。例如,由于具有优异的力学和热性能,泡沫材料在不同航空应用中的使用日益增加。电动汽车的电池中也包含多孔结构。

模拟多孔介质中的达西流和非达西流
2020年 2月 24日
了解多孔介质中流动建模背后的理论,包括Kozeny–Carman、Forchheimer、Ergun、Burke–Plummer和Navier–Stokes方程。
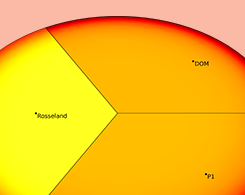
参与介质中辐射传热的 4 种计算方法
2019年 5月 22日
离散坐标法,P1 近似,Rosseland 近似,或者比尔-朗伯定律:你应该用哪一个来分析参与介质的传热?

如何在地下水流模型中使用井特征
2017年 8月 21日
对于地下水流建模,使用井特征可以更加容易地设置和划分网格。了解如何利用此特性的设置和功能。
