COMSOL Multiphysics^® 能求解氢原子吗?

量子力学开启了现代物理学时代，特别是在 20 世纪的前几十年。公平地讲，没有其他理论能像量子力学那样深刻地动摇我们对真实世界的理解。这篇博客，我们来看看量子力学中最重要的精确结果——氢原子的基态和最初的几个激发态，并讨论如何使用 COMSOL Multiphysics^® 软件重现这些结果。

量子力学与原子结构

原子由一个带正电的原子核和绕核运动的带负电的电子组成，它的存在和稳定性无法用经典物理学解释。加速运动的带电粒子（如绕原子核运行的电子）会产生电磁辐射，因此会逐渐失去能量，导致电子不可避免地坍缩到原子核中。量子力学通过确定束缚电子只能拥有某些固定的能量值来解决这个难题，从而防止了辐射导致的能量的逐渐损失。这在数学上类似于驻波：波必须是单值的，仅对于某些固定波长（例如：能量）是可能的。


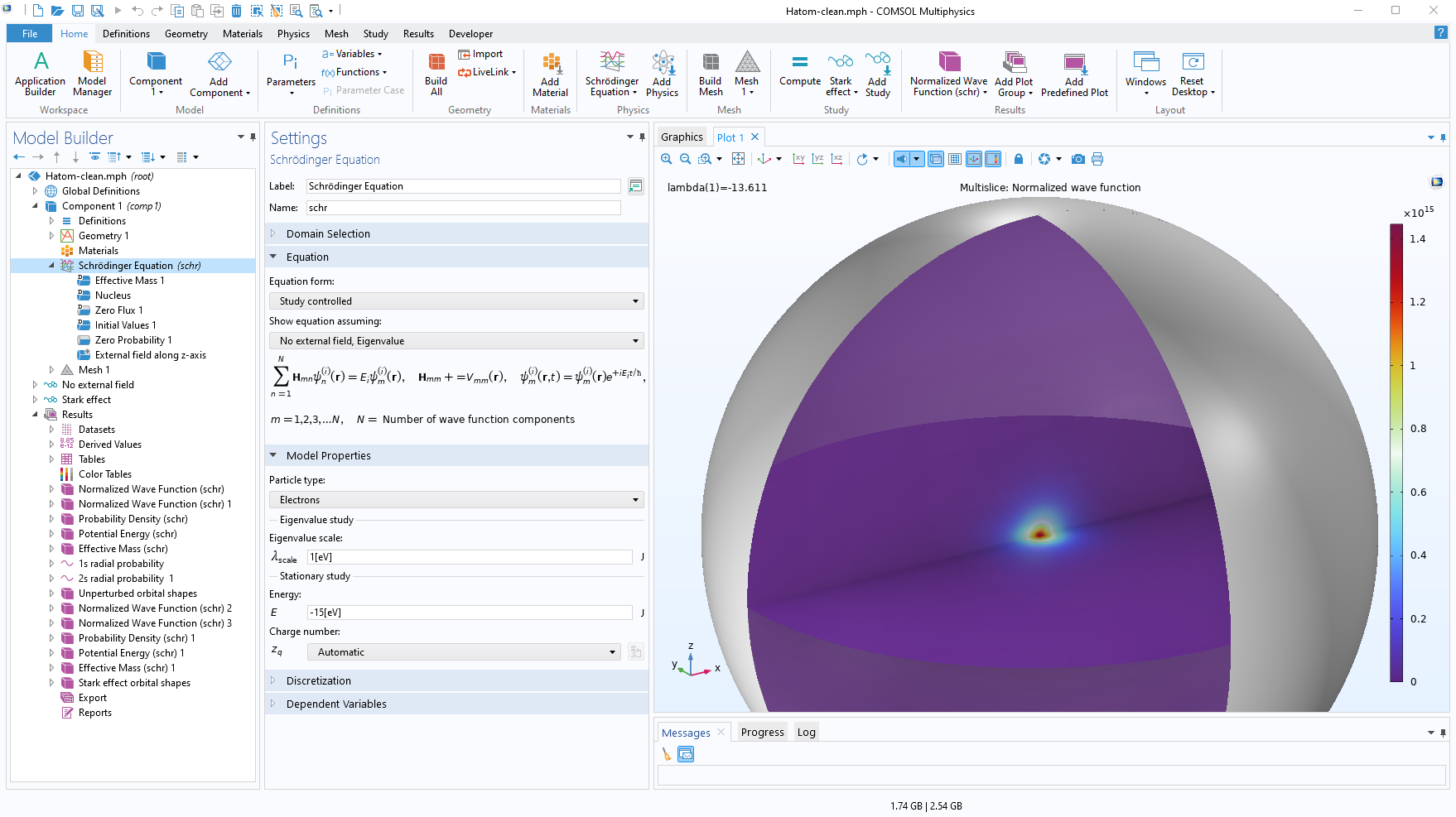
COMSOL Multiphysics^® 用户界面与显示氢原子模型（将在下一节深入讨论）的 图形窗口。

量子力学能量的一个早期证明是通过光谱测量对氢的结果（见下文）进行实验确认。自那以后，量子力学就成为了物理学中得到验证最多的理论。

与多电子原子不同，只有一个电子的氢原子可以由与时间无关的薛定谔方程很好地近似描述:

式中，\hbar, m_e, e, 和 \epsilon_0 分别是约化普朗克常数（Planck constant）、电子质量（约化质量）、基本电荷和真空介电常数。要求解的因变量 \psi(\mathbf{r}) 是波函数：一个复杂的标量场，其范数 |\psi(\mathbf{r})|^2 给出找到电子的概率 \mathbf{r}。左边的算子 \hat{H}是哈密顿量（Hamiltonian），基本上对应于系统的总能量。拉普拉斯算子给出了电子的动能，而势能则简单地由原点处带正电的原子核（在这里指只有一个质子）引起的库仑势给出。薛定谔方程以未知总能量 E 的特征值问题的形式存在，并且可以通过该行业的常用工具精确求解：变量分离和级数展开。得到的本征态由三个整数，或量子数 n,l 和 m 标记，其中 n,l\in \mathbb{N}, l \leq n 和 m=-l, \cdots, 0,\cdots,l。使用分别表示极角 \theta 和方位角 \phi 的球极坐标（与在 COMSOL^® 中使用的定义相同)，可以将它们表示为

式中，R_{nl} 是径向波函数和 Y_l^m(\theta, \phi) \propto P_l^m(\cos\theta) e^{im\phi}，用勒让德多项式（Legendre polynomials）P_l^m(\cos\theta) 表示，被称为球谐函数。本征能量仅取决于主量子数，n:

式中，R_H\approx13.6057\,\mathrm{eV} 被称为里德伯常量(Rydberg constant)。下表给出了前几个本征态的显式表达式。

在这里，我们使用玻尔半径 a_0 \equiv \frac{\hbar^2}{m_ee^2}\approx 52.9\,\mathrm{pm} 作为一个方便的长度尺度。 从上表可以看出，对于更高的主量子数，存在多个具有相同能量的态。这种简并性源于势能的高度对称形式。

超出氢的情况会变得非常复杂。如果没有确切的结果，微扰计算会变得极其繁琐，因此数值计算是最可行的前进方向。传统的原子和分子结构的数值研究是基于变分法和处理电子费米子性质的方进行的，例如 Hartree–Fock 方法。应该选择一组基函数来展开本征态，然后将展开系数上的能量最小化。

COMSOL Multiphysics^® 中的氢原子

对于氢原子的示例，薛定谔方程只是 3D 中复值标量场的偏微分方程，因此允许基于有限元法求解特征值问题。COMSOL Multiphysics^® 的一个附加产品，半导体模块内置了一个薛定谔方程 接口（也称为 schr，如下表所示），我们可以使用这个接口来创建氢原子模型，所需的设置非常简单。

设置一个半径为A_0\equiv 15a_0 的球体，并在薛定谔方程 接口修改默认节点（有效质量和电子势能) ，使有效质量等于 m_e（在这个模型中我们没有周期性晶格），电子势能等于原子核的库仑势。这里唯一需要的边界条件是 \psi \rightarrow 0 且 r\rightarrow \infty，即由于我们正在寻找束缚态，所以用薄层包围球体并将其定义为无限元域。为了提高计算速度，我们使用了在径向方向上逐渐变粗的网格。 最后，我们将能量标量指定为 eV，并以 -15 eV 作为特征值搜索的起点。

下表显示了前两个主量子数获得的本征能量以及它们的理论值。

请注意，特征值取决于所使用的网格，因此我们始终建议运行网格细化研究，以获得可靠的结果。为了了解本征态或轨道的形状，用 3D 等值面图绘制它们，如下图所示。

未受扰动的氢的轨道形状，使用一系列位移的 3D 等值面图进行可视化。

我们采用了原子物理学中广泛使用的标记: 1\mathrm{s}, 2\mathrm{s}, 2\mathrm{p}_x,\cdots。可以看到 s 态是径向对称的，而每个 p 态沿三个相互垂直的一个轴具有圆柱对称。对于波函数为球对称的 s 态，径向概率密度有一个简单的解析形式，其定义如下:

解析结果与模拟结果的比较如下图所示。

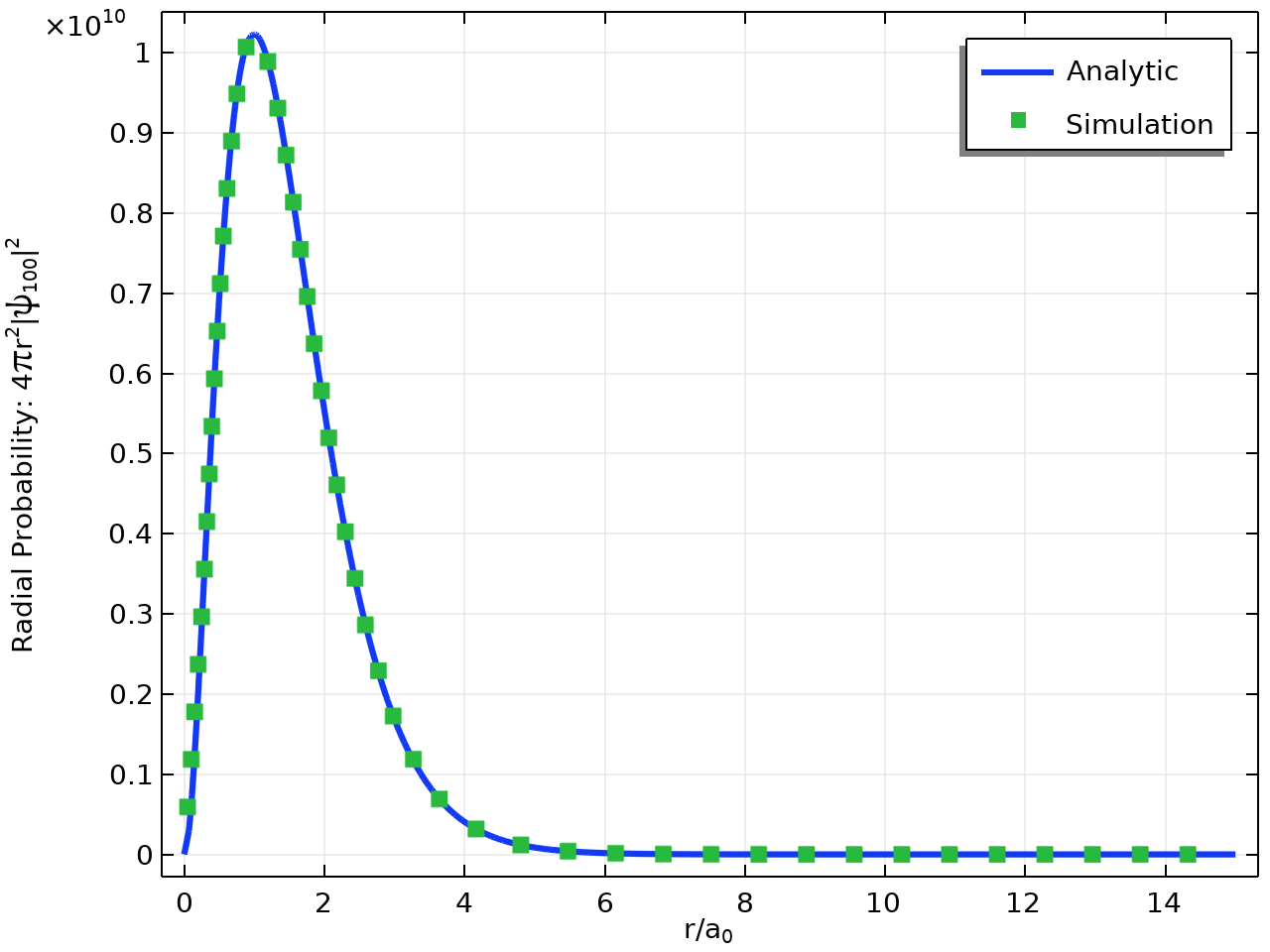
1\mathrm{s} 状态（基态）的径向概率：精确结果（线）和使用 COMSOL^® 获得的数值结果（点)。

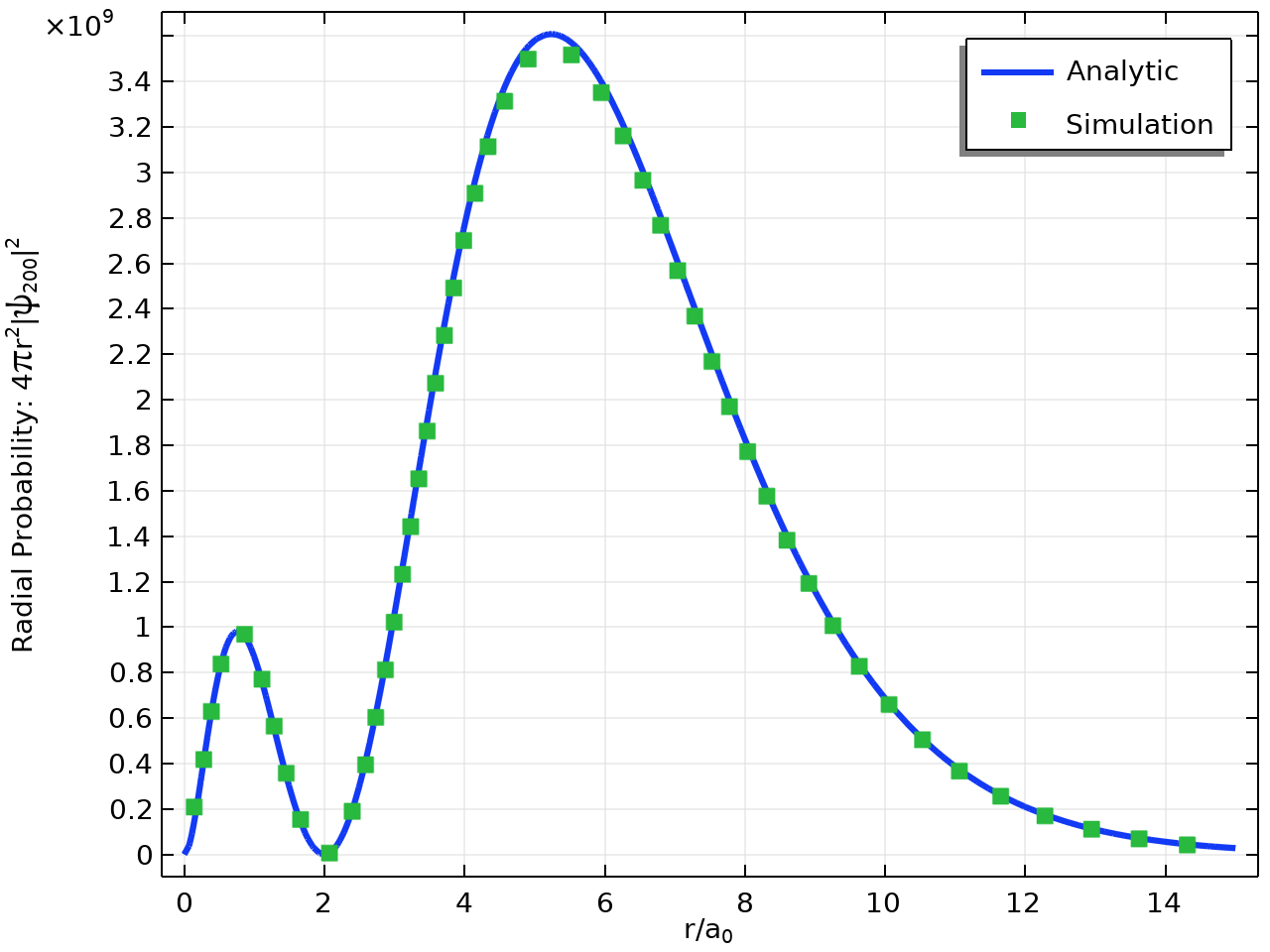
2\mathrm{s} 状态（第一激发态）的径向概率：精确结果（线）和使用 COMSOL^® 获得的数值结果（点)。

斯塔克效应

假设有一个沿 z 轴方向的外部电场，提升了我们前面讨论的简并性，那么应该将下列项添加到哈密顿量中:

由此产生的薛定谔方程无法再精确求解，因此我们不得不求助于微扰理论。对于初级，1\mathrm{s}, 2\mathrm{p}_x 和 2\mathrm{p}_y 状态不会改变能量（或形状)。然而，外部场引起 2\mathrm{s} 和 2\mathrm{p}_z 状态混合，导致两个分裂的能级；这是一个斯塔克效应的例子，可以在光谱测量中通过实验观察到。对能级的修正可以用下式计算:

另一方面，使用 COMSOL^® 在数值上找到 Stark 分裂就像没有外部场一样简单：如果简单地添加另一个电子势能 节点到我们的模型，可以很容易地获得分裂能级以及相应的轨道形状。为了使效果清晰可见，我们使用了非常高的外场 \sim2\times10^{8}\mathrm{V/m}。

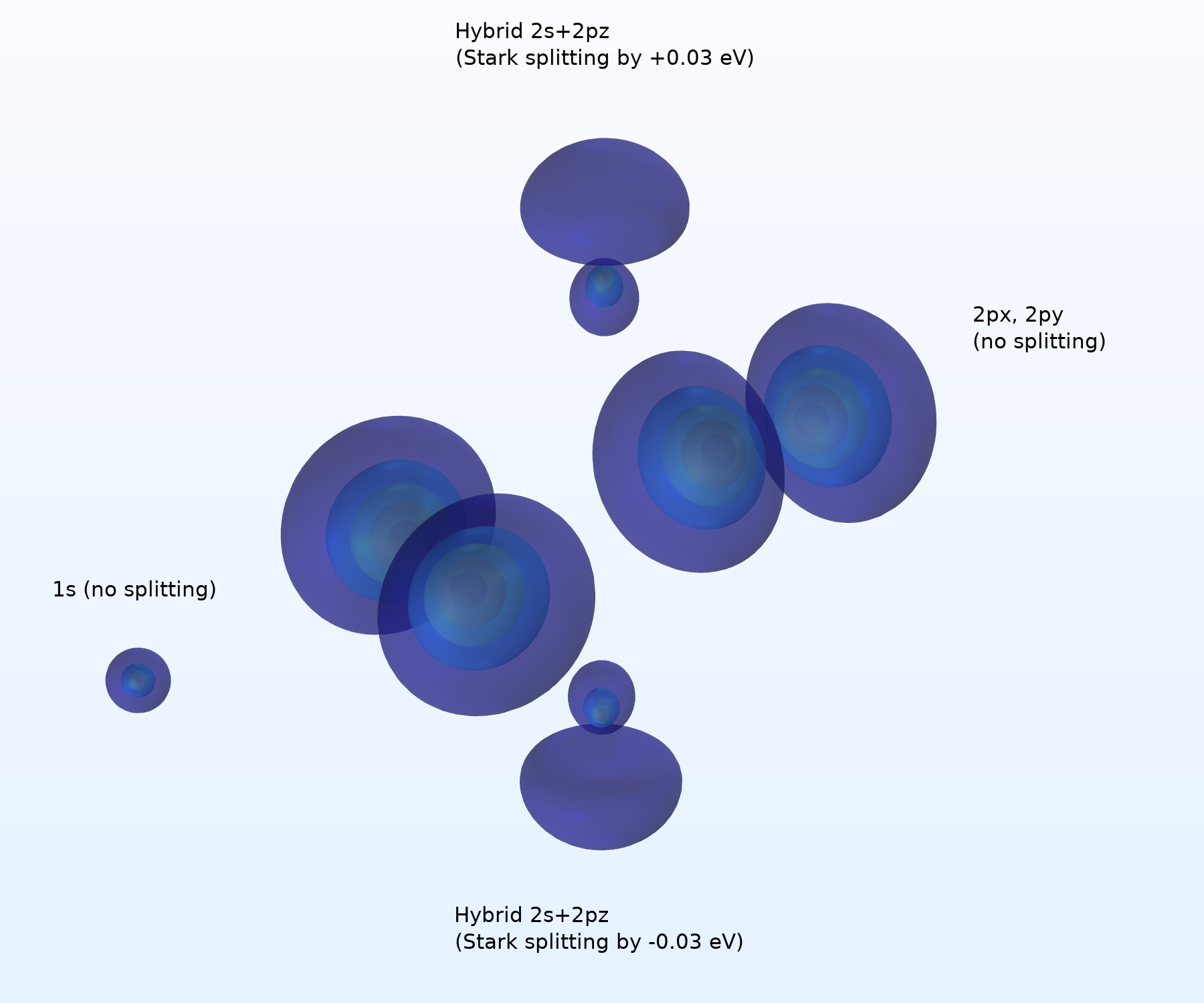
在 z 轴方向上存在外部电场时的轨道形状。

结束语

这篇博客，我们通过氢原子讨论了量子力学的一些基础知识，并了解了如何使用 COMSOL Multiphysics^® 中的薛定谔方程 接口再现结果。然而，这里介绍的模型不仅仅具有教学意义，它还可以作为一个验证软件功能的有用示例，并且与半导体物理学直接相关，其中掺杂态通常使用类氢波函数建模。您可以将这个模型和这篇博客作为参考，在 COMSOL^® 中创建更加精确的量子力学模拟。

如果您对进一步探索氢原子感兴趣，请单击下面的按钮，下载文中讨论的示例模型:

拓展学习