我们能听出鼓的形状吗？

半个世纪前，Mark Kac 做了一个有趣的讲座，讲座内容基于十年前他从 Bochner 教授那听到的一个问题：“我们能听出鼓声的形状吗？”他把讲座的重点放在特定的(待定)一组特征值能否确定振动鼓膜形状。特征值问题已经解决了，在这里，我们通过考虑一些有趣的物理效应，探索这个问题中“听”的部分。

原始特征值问题：对同频鼓的探索

让我们想象一下鼓面的结构：将鼓膜拉伸，套在一个刚性支架上，从而围成一个二维区域。膜的振动是由波动方程（亥姆霍兹方程）来描述的，由于膜的外围被刚性支架所约束，因此由狄利克雷边界条件来描述。在这种情况下，波动方程存在一组离散的解，称为正则模态或特征模态，每种模态下的振动都会具有一种特定频率，这些特定频率被称为特征频率。

最低特征频率定义了鼓的基音，比如可以是标准音 A (440 Hz)。较高特征频率，用音乐术语来说也叫泛音，决定振膜的音色和音质。Kac 的讲座将我们的关注点引向了特征频率：是否有可能制作出形状不同而特征频率却相同的两个鼓面？这一问题可解释为，尽管两只鼓的形状不同，但有完全相同的特征频率（同频），同时用耳朵听时，具有相同的音色和声音。

Kac 对特征频率在非常高的频率极限条件下的渐近行为进行了评论，并将物理学和数学的多个分支联系到一起，从而为直观地理解这一问题提供了一个基础。但这一独特问题（在二维平面空间）始终找不到解决方法。直到二十多年以后，Gordon、Webb 和 Wolpert 终于建立了两个特征值相同的多边形（见 参考文献 1 和 参考文献 2），问题才被解决。

两个多边形的本征值可以利用数值进行计算，在我们的模型库中的同频鼓模型展示了这一结果。

下面的图像列出了具有同一组特征频率的两个多边形的前三种正则模态。

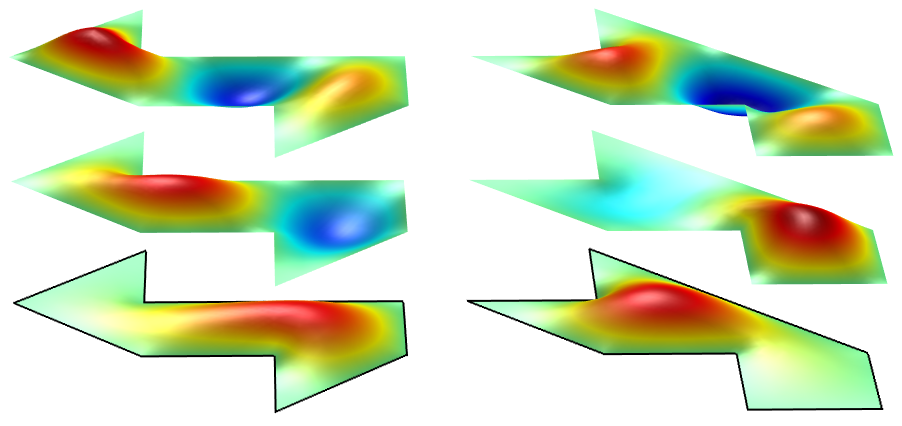
在 Gordon 和 Webb 的易于阅读的有关这个主题的介绍性文章 (参考文献3) 中，他们认为这种不同形状的同频鼓应该是特殊情况，而不是普遍规则。换句话说，他们认为，在一般情况下，人是能够听出鼓的形状的，除非其形状是特制的，与另一个形状的鼓同频，就像上面描述的两个多边形一样。

在下面的讨论中，通过考虑各种物理机制，包括声音的产生和检测，我们将仔细研究这种特殊形状。我们会发现，当考虑相关的物理效应时，实际上我们可以通过鼓的声音来区分两种鼓的形状，即使它们是特制的，有着相同的一组特征频率。

膜运动的激发

我们将检测的第一个效果是鼓膜振动模式的激发。由于音色是由正则模态的相对振幅组来决定，因此如果想让两只鼓听起来相同，只有一组特征频率相同是不够的。同时还需要每个特征模态具有相同的相对振幅，这可能并不容易实现。

我们还是以上面提到的两种多边形鼓为例，用鼓槌击打鼓面上的一些任意点，一次击打一个点，如下图所示：

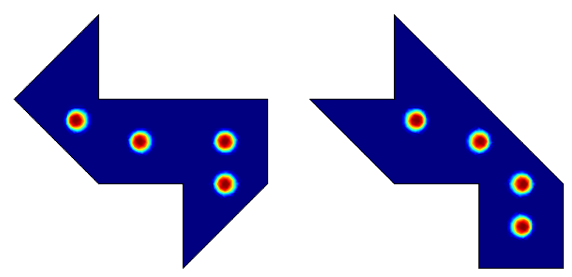
每个打击的点都在鼓中间的某个位置，如果给一个孩子这样一只鼓和一个鼓槌，孩子可能会本能地选择击打这些位置。我们使用 COMSOL Multiphysics 仿真软件来计算每个位置的频率响应，并在下面的图中标绘出来。

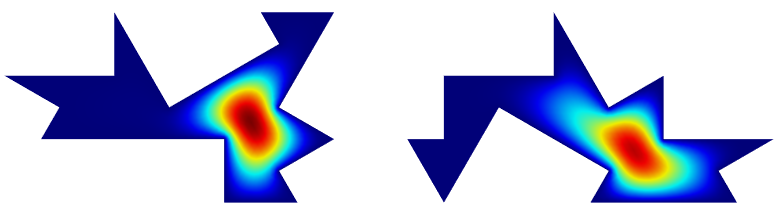
我们开始只考虑一只鼓的频率响应，比如左边那只鼓。下图标绘出了左鼓的频率响应。

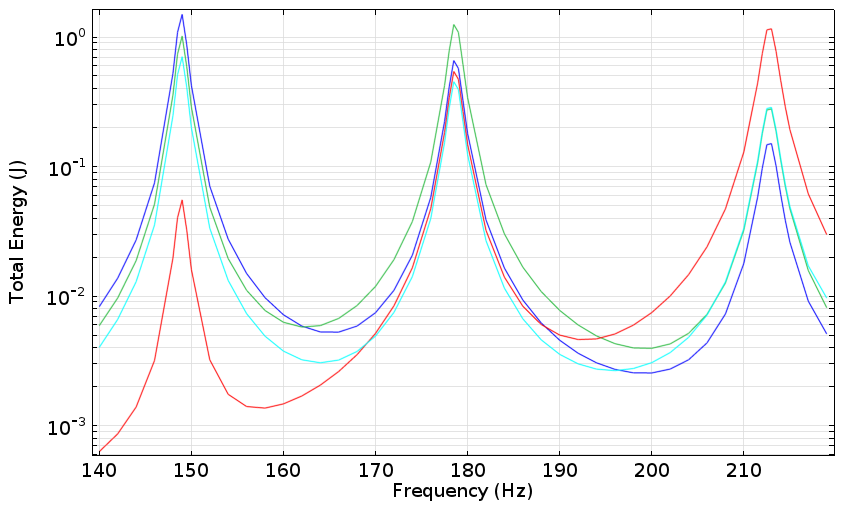
正如我们先前所暗示的那样，鼓槌击打鼓面位置的不同，会造成鼓的声音不同。我们可以在前三种特征模态中看到不同的能量分布，这将产生不同的音色。当然，对打击乐手来说，这是一个众所周知的事实。用一只鸣钟产生两个不同的音调，也是利用了相同的原理，两千多年前出现的古乐器——编钟，很好地证明了这一点。

现在我们知道，我们甚至不能让一只鼓一直产生同样的声音，除非我们知道鼓槌应该确切击打在哪一点。那么是否有可能让两只不同的鼓产生同样的声音呢？

在下面的图中，我们增加了第二只鼓的频率响应曲线（用虚线表示）。当我们审查下图时，可以明显看到，在三种特征模态下，没有一条虚线能和实线完全吻合。换句话说，两只鼓确实会发出不同的声音，即使它们同频谱，有着相同的特征频率组。

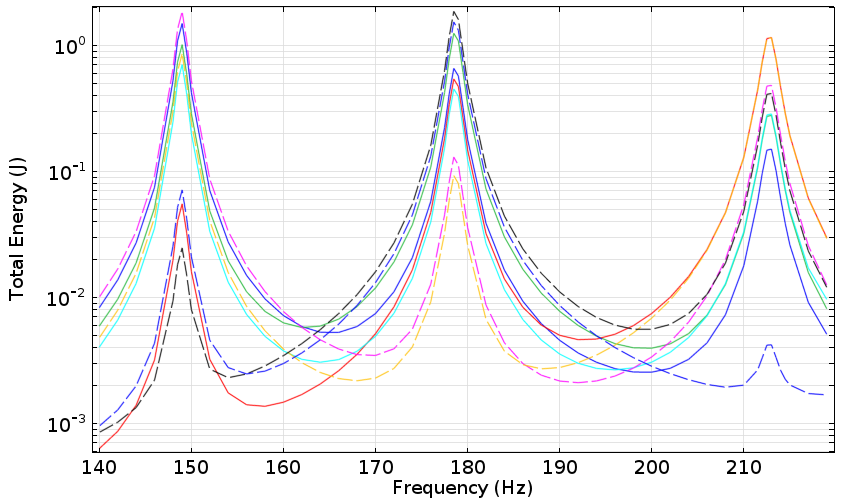
当然，鼓面上还有很多击打位置，我们没办法穷举搜索所有可能的位置组合方式。然而，这个简单的例子已经可以说明，要使鼓的声音相同并不容易，由于鼓膜具有不同的振动模式，导致鼓具有不同的能量耦合强度。

同频鼓

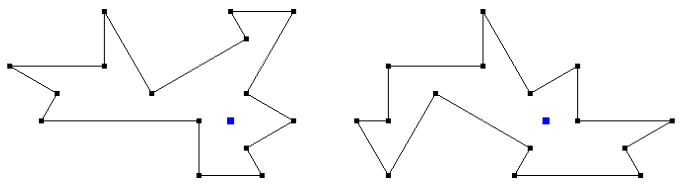
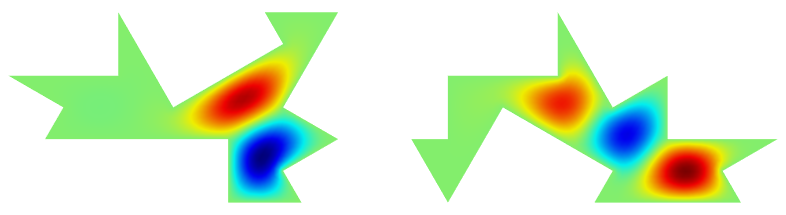
数学的魔力带给我们的惊奇从未停止。两个同频谱多边形的论文发表后不久，Buser、Conway、Doyle 和 Semmler 构建了一对区域，不仅同频（具有相同的频率），而且同音：即在区域内有一个特别的点，“这些点处相应的归一化的狄利克雷本征函数，有相同的值”(“参考文献 4“)。换句话说，如果用鼓槌击打每只鼓的特殊点，两鼓对应的每对特征模态将具有相同的幅值，两鼓听起来就会相同。

下图显示的是用数值方法计算出的前几种正则振型的形状：

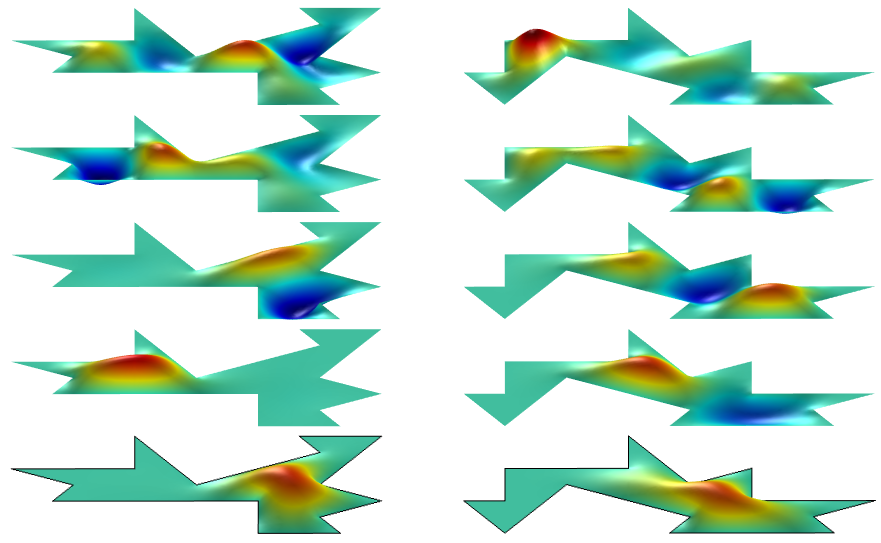
在下面的示意图中，每个区域的特殊点用一个蓝色的正方形标记出来：

在下面的图中，我们标绘出了计算出的两只鼓的频率响应，这些频率分布在一个狭窄的高斯区域，负荷集中在每一个特殊点的位置：

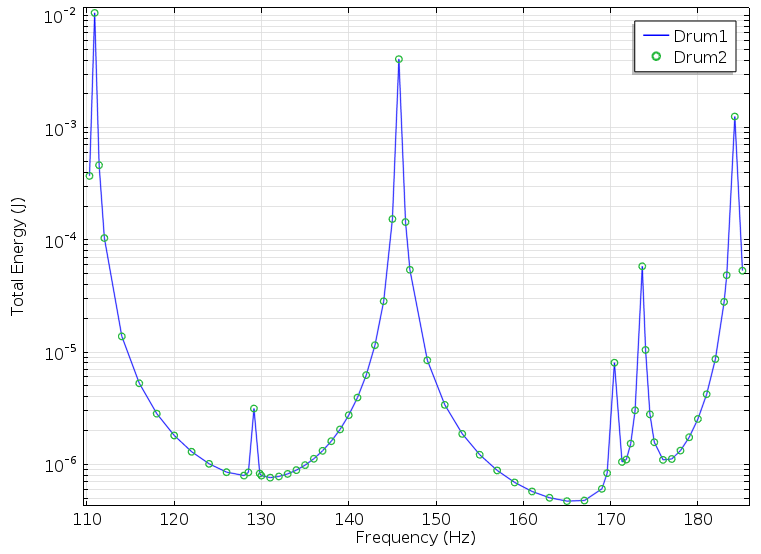
两种频率响应曲线（蓝色曲线和绿色圆圈）完全吻合，是不是非常令人惊奇？有了这样一个完美匹配的振动能谱，是不是两只鼓的声音就会完全一样了呢？让我们继续探索之旅，探索并找出更多的物理效应。

声波在不同方向的传播

我们的耳朵无法直接感觉到膜的振动。人对声压的感觉，依靠的是在空气中传播的声波。我们可以在室外放置两只同频鼓，从而保证声音能够传播地很远，同时没有明显的反射。在这种情况下，我们可以使用 COMSOL Multiphysics 很容易地计算出声波频谱，从而找到我们的耳朵真正听到的内容。

让我们来看看三种具有最高能量的振动模式，上图所示的频谱图中，这三种振动模式处在约 111、146 和 184 Hz 的位置。为了方便，我们分别称为第一、第二和第三模式，三个模式之间还有其他模式，但因为它们的能量相对较低，我们可以将其忽略。

下面的极坐标图比较了计算得出的两只鼓所处的平面内的声压值（单位为分贝），两鼓相距几米远。

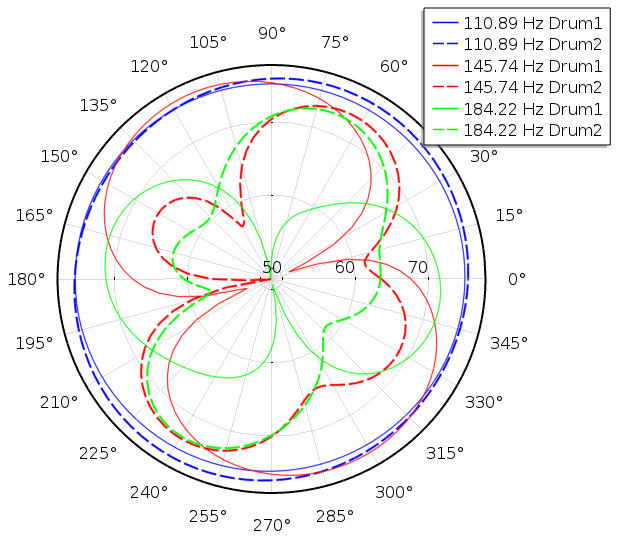
我们看到，第一模式产生的声压场，一般来说与方向无关（蓝色实线和点线）。这并不奇怪，因为每只鼓的第一振型看起来非常像一个单极源：

另一方面，从每个鼓的第二或第三模式得到的声场，其方向性是很明显的，两只鼓也是完全不同的。例如，对于第二种模式，从鼓1得到的声场看起来像一个偶极子场（红色实线），而从鼓 2 得到的声场更复杂（红色点线）。这一结果与我们在两只鼓的振型中所看到的再次匹配：

真正决定我们所感知到的音色的，是高频模式（泛音）振幅与最低频模式（基调）振幅的比值。因此，在下图中，我们在各采样方向上，绘制了第二模式和第三模式的振幅与第一模式振幅的比值：

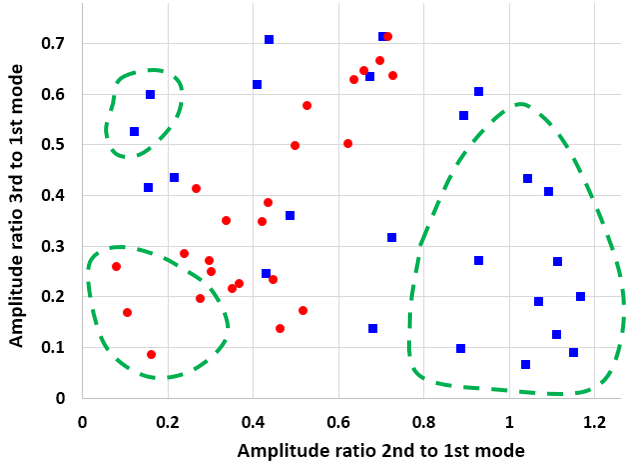
蓝色的方点是从鼓 1 得到的比值，红色圆点是从鼓 2 得到的比值。我们可以将上图看作是一个音色图：如果图上的两点距离比较近，那么它们听起来就相似；相反地，如果图上的两点相距甚远，那么它们就各自有着独特的音色。绿色虚线圏起的区域可定性说明，在一些方向上，每只鼓可以产生一系列其他鼓无法产生的音色。

只要允许听众绕着鼓走动，假设蒙住眼睛，他们也会听到明显不同的音色区域，从而将两只鼓区分开来。因此，尽管两只“同音”鼓在它们的振动模式下具有相同的能量谱，由于振型的不同，以及能量随声场在空气中传播的不同，在一些方向上，声能量谱可以完全不同。这是两只鼓的声音听起来不同的原因。

空气负荷导致特征频率发生变化

在以上的分析中，我们忽略了空气作用于鼓膜上的反作用力，即所谓的空气负荷效应。事实证明，对一只真正的鼓来说，这种效应是非常显著的，因为，在鼓膜所处的整个区域，周围空气都有着推动和拉动鼓膜的作用。

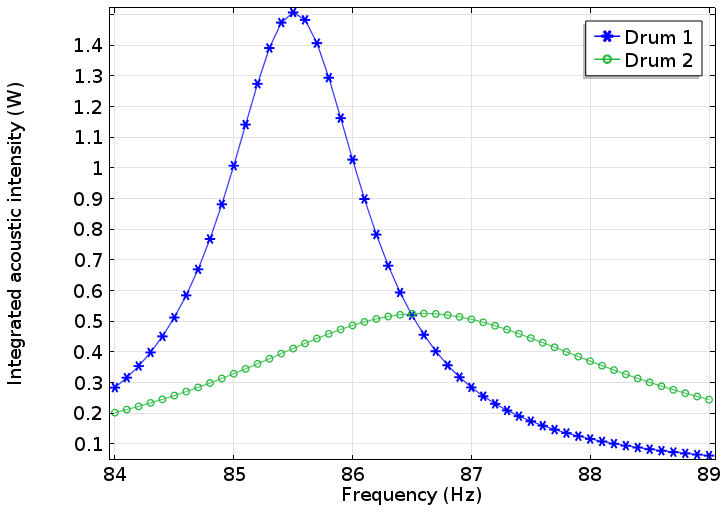
我们可以利用声学结构边界多物理场，结合 COMSOL Multiphysics 的特性，模拟这种效果。我们发现，以第二模式的特征频率为例，我们之前讨论的频率值 146 Hz 会变为 86 Hz。此外，两只鼓的特征频率的变化是不同的。一只鼓的频率变为 85.6 Hz，而另一只鼓变为 86.8 Hz。这种差异导致两只鼓的高音差异为 23 音分，在将两只鼓并排放置做比较时，这种差异非常明显。

因此，这两只鼓不仅是音色不同（在一定范围内的方向上），当我们把空气载荷效应考虑进来时，它们也有不同的绝对音高。

下图显示了两只鼓在这种模式下的频率响应。从图中可以不仅可以清楚地看到共振频率的差异，还可以看到共振宽度的差异。毫无疑问，在我们看来，有着这样不同的频率响应，两只鼓产生的声音将非常容易区分。

结束语

发现具有相同一组特征频率的同频鼓，以及在一个特殊点击鼓时具有相同振动模式功率谱的同频鼓，在数学领域是一个伟大的成就。然而，这些现象只发生在真空中，那里并没有声音。一旦我们把鼓放到空气中，由于空气载荷效应和膜将能量转化为声波传播时特有的方向性，两只鼓的声音就会不同。

在演讲中，Kac 讲述了上世纪早期的一个故事：Lorentz 呼吁数学家注意黑体辐射理论中的特征值问题，Weyl 响应号召，并以非常高频率下特征值具有渐近性的定理，作为证据。

在本文的讨论中，我们可以再次运用数学家朋友的帮助，即使主题可能不像黑体辐射和量子力学那样重要。如果考虑方向性和空气负荷作用，是否有可能构造出形状不同、但听起来相同的同频鼓？如果将这一问题作为一个优化问题来解决，将问题的解看作是一组可听频率的有限集，问题可能是有解的。

当然，计算成本会很高，得到的结果也只是近似值。上面提到的论文中给出了很多解，如果能得到一个类似的简洁的解析解，将是更好的。我希望这能引起正在阅读的数学家的兴趣。

参考文献

1. One cannot hear the shape of a drum.BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY,Volume 27, Number 1, July 1992
2. Isospectral plane domains and surfaces via Riemannian orbifolds，Inventiones mathematicae,110,1-22(1992).
3.”You can’t hear the shape of a drum”, American Scientist, vol.84 (1996), pp.46–55.
4. Some planar isospectral domains.International Mathematics Research Notices, Volume 1994, Issue 9, 1994, pp 391–400, https://doi.org/10.1155/S1073792894000437.