电磁学 博客文章

如何模拟细胞膜的电穿孔现象
2025年 12月 11日
电穿孔技术被用于在细胞膜上制造孔隙,以允许大分子(如药物)进入细胞。阅读博客,深入了解细胞膜电穿孔的关键机制,以及如何在 COMSOL 中对其进行模拟。

使用深度神经网络代理模型模拟空间等离子体
2025年 11月 20日
这篇博客文章介绍了一种基于玻尔兹曼方程的解进行训练的深度神经网络代理模型,可用于高效模拟空间等离子体。
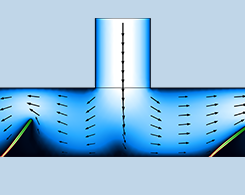
模拟无阀微泵机理
2025年 8月 18日
无阀微泵是许多微流体系统的组成部分。模拟可用于研究这些部件中发生的流体-结构相互作用,以提高其性能。
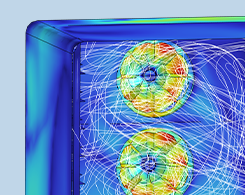
食品安全领域的5 个仿真实例
2025年 5月 7日
2024 年消费者对食品安全的信心降至历史最低点,这使得企业确保其产品安全变得至关重要。了解建模和仿真如何帮助企业确保产品安。

激光雷达技术在自动驾驶汽车和扫地机器人中的应用
2025年 5月 5日
未来,自动驾驶汽车会普及吗?探索如何使用射线追踪研究使其能够感知周围环境的技术。

利用对称性进行射频和波动光学模拟
2025年 4月 9日
我们可以通过利用电磁波模型可能具有的任何对称性来简化模型规模,并减少计算复杂度。点击此处,了解如何操作。

模拟质子疗法中的笔形束扫描喷嘴
2025年 3月 6日
在质子治疗中,高能质子束用于向治疗区域发射电离辐射。了解粒子追踪仿真如何帮助推动这种治疗。

模拟螺栓连接处的电接触电阻
2024年 12月 16日
COMSOL® 软件6.3 版本新增了一个新的边界条件,在设置结构力学问题时可以简化工作流程。阅读博客,探索这个功能的实际应用。



