在设计电化学电池时,我们需要考虑电解质和电极中的三类电流分布:一次分布、二次分布 和三次分布。不久之前,我们介绍了电流分布的基本理论;本文则以线电极为例,详细解释不同的电流分布类型,帮助你在 COMSOL Multiphysics 中选择合适的电流分布接口,顺利执行电化学电池仿真。
三种电流分布接口
与上一篇博客文章一样,我们可以借助线电极模型的案例比较三种电流分布接口。下方是线电极的几何结构示意图:
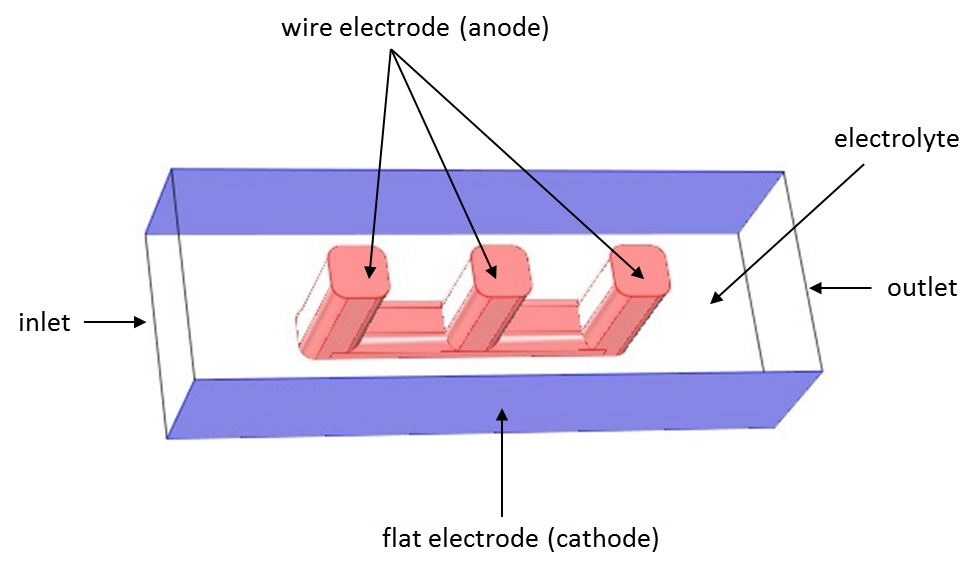
使用 COMSOL Multiphysics 求解的线电极模型。电解质可以在导线和平坦表面之间的开放空间内流动。
本文提及的三种电流分布情形采用了相同的几何模型:在两个平坦的电极表面之间放置一个线电极结构。该电化学单元电池可视为一个体积更大的线网格电极中的一个单元,后者是许多大规模工业生产过程中常见的电化学电池装置。
回顾基本方程
以下是我们在上一篇博客中详细说明的基本方程式:
Nernst-Planck 方程:
(1)
包含 Nernst-Planck 方程的电流密度表达式:
(2)
一般电解质电流守恒:
一次电流分布
一次电流分布仅适用于解释溶液电阻造成的损耗,而忽略了电极动力学和浓度依赖性效应造成的损耗。它假定电解液中的电荷转移遵守欧姆定律。在这里,我们做出了两个假设:第一,电解质是电中性的,它抵消了对流项在表达式(2)中对电流密度的贡献;第二,电解质的成分变化微不足道(即分布均匀),这抵消了扩散项在表达式(2)中对电流密度的贡献,允许我们将离子强度看作一个常数。由此一来,表达式(2)的剩余项即为欧姆定律用于描述电解质电流密度。
我们认为,电极-电解质界面上的电解反应发生得非常快,以至于可以忽略电极动力学的影响,因此,电极-电解质界面上的电势差基本不会偏离平衡值。换句话说,没有活化过电位,而且通过电解会产生任意的电流密度。由此可见,一次电流分布仅取决于正极和负极的几何构造。
COMSOL Multiphysics 的一次电流分布 接口定义了两个相关变量:一个是电解质电势(\phi_l\),另一个是电极电势(\phi_s\)。基于上述的一次电流分布假设,可得以下方程:
电极:\textbf{i}_s = -\sigma_s\nabla\phi_s\ 和 \nabla\cdot\textbf{i}_s = Q_s
电解质:\textbf{i}_l = -\sigma_l\nabla \phi_l\ 和 \nabla\cdot\textbf{i}_l = Q_l
电极与电解质界面:\phi_s-\phi_l = E_{\mathrm{eq},m}
其中,\sigma_l 表示电解质的电导率,根据上述假设它是一个常数。下标 s 代表电极,l 代表电解质。E_{\mathrm{eq},m} 表示反应 m 的平衡电位。
在下图中,我们展示了线电极示例的一次电流密度分布。如您所见,电流密度分布在直面负极板的导线的拐角处,在导线结构的中心区域则趋近于零,原因是从几何结构上该区域与负极隔开了。
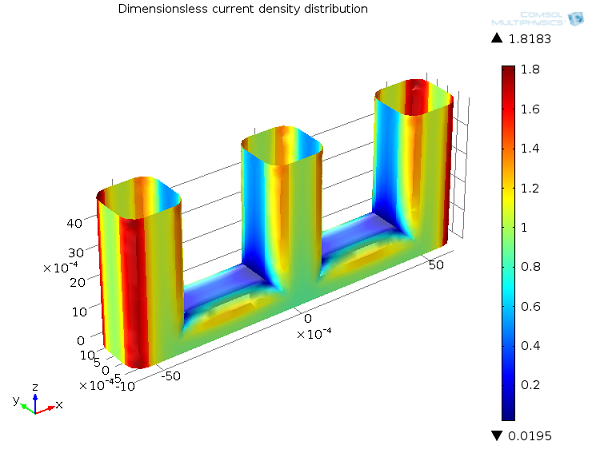
一次电流分布,Ecell = 1.65 V。正极上的电流密度分布(无量纲)。
何时使用一次电流分布 接口?
如果电池的电解质浓度(相对于电流密度)较高,或者经剧烈搅拌混合后,电解质浓度可以假设为均匀。并且,电化学反应速度非常快,以至于反应电阻的大小与电阻损耗(溶液电阻)相比可忽略不计。如此,便可以使用一次电流分布来模拟电池。
上述条件的应用之一是在施加外加电流阴极保护系统的阳极上,与此同时,在一次电流密度分布接口中,我们可以将相当于氧还原反应中受质量传递限制的电流,以恒定电流的条件设为阴极的边界条件(参照案例)。这也是对反应速度相对较快的电化学过程的一个有效近似,例如氯碱工艺流程中氯离子的快速氧化。
由于一次电流分布 接口易于求解,且不涉及非线性动力学表达式,因此通常适合于计算基准近似结果,为处理较复杂的模型做好准备。
二次电流分布
二次电流分布用于解释电极动力学和溶液电阻的影响。它关于电解质的组成和特性的假设与一次电流分布是一致的,也就是说电解质电流同样遵守欧姆定律。一次和二次电流分布的区别在于对电解质和电极界面上的电化学反应的描述。
二次电流分布引入了电极动力学的影响;由于电解反应速率有限导致额外的阻抗,电位差可能偏离其平衡值。实际电位差和平衡电位差的差值即活化过电位(\eta)。因此,你会发现一次电流分布 和二次电流分布 接口的域方程完全相同,但是由于过电位的存在,电极-电解质界面的电位方程式存在差别:
电极:\textbf{i}_s = -\sigma_s\nabla\phi_s\ 和 \nabla\cdot\textbf{i}_s = Q_s
电解质:\textbf{i}_l = -\sigma_l\nabla \phi_l\ 和 \nabla\cdot\textbf{i}_l = Q_l
电极与电解质界面:\eta_m = \phi_s-\phi_l-E_{eq,m}
在二次电流分布 接口中,由于电化学反应而产生的电流密度被描述为过电位的函数。物理场接口可以使用电流密度和过电位之间的任何关系,例如 COMSOL 的常用内置选项 Butler-Volmer 方程式(3)和 Tafel 方程式。
(3)
上述 Butler-Volmer 方程针对反应 m 规定:i_{loc,m} 代表局部电荷转移电流密度,i_{0,m} 代表交换电流密度,\alpha_{a,m} 代表阳极电荷传递系数,\alpha_{c,m} 代表阴极电荷传递系数。R 是通用气体常数。这个方程式描述的情形是:单电子的电荷转移是净电荷转移反应的速率控制步。我们可以以描述均质化学反应的 Arrhenius 方程进行类比,从而推导出方程式,前提是假设带电物质的自由能会受到电位的影响。因此,活化能将随电极-电解质界面的电位差而变化。
根据下方公式,将全部电极的反应电流之和用作电极和电解质域之间边界上的电流密度条件:
附加电容电流 i_\mathrm{DL} 产生于双电层的充电和放电过程。
一般情况下,通过活化过电位来解释电极动力学的影响,往往会使电流分布更加均匀。下图中的线电极示例说明了这一点。
与一次电流分布相比,二次电流分布更加平滑,最小值与最大值之间的差异更小。引入了活化过电位的影响后,局部高电流密度将在电极表面引发高的局部活化过电位,自然导致电流流向其他的路径。换句话说,你可以理解为电化学反应以有限的速率进行。在某些区域,反应动力学受到了限制,因此表面的电流密度分布会比不受限制的快速反应的情形更加平滑。
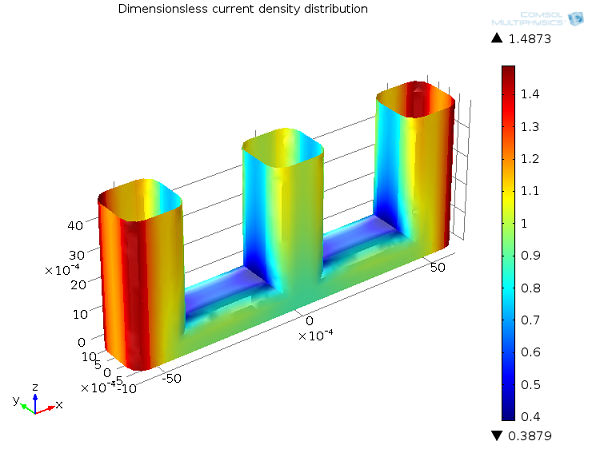
二次电流分布,Ecell = 1.65 V。正极的电流密度分布(无量纲)。
何时使用二次电流分布 接口?
二次电流分布 是电化学工业应用建模的“主力”接口。你可以将二次电流分布用于电池建模,前提是电解质充分混合或浓度相对较高,因而可以忽略浓度过电位,若电极动力学引起的损耗与电阻损耗相比不可忽略,则不可行。众所周知,在工业应用中充分混合高浓度的电解质不是一个难题。你还可以将使用二次电流分布 接口作为电化学电池仿真的第一步,先计算出活化损耗,之后再引入浓度依赖反应动力学。
三次电流分布
三次电流分布用于解释电解质组成和离子强度的变化对电化学过程的影响,以及溶液电阻和电极动力学的影响。为此,它完整求解了 Nernst-Planck 方程(1),借此描述每一种化学物质通过扩散、迁移和对流的质量传输。此外,物质的浓度需要满足电中性假设。电化学反应的动力学表达式解释了活化过电位和浓度过电位,这意味着在电极-电解质界面,反应物的耗尽会导致电解反应的速率受到传输的限制。这也暗示了,电解液中的全部离子和全部活性物质都必须包含在模型中。
与一次和二次电流分布不同的是,三次电流分布中的电解质电流密度不再假定遵循欧姆定律。根据方程式(2),电中性的施加仍然意味着对流通量对电流密度没有贡献,但现在不能忽视电解质浓度变化带来的影响。因此,方程式(2)中的扩散项可能是非零项。
在电极-电解质的界面上,电荷转移反应的电流密度不仅被表示为过电位的函数,也是界面处电活性物质浓度的函数。相对于取决于单电子电荷转移步骤的反应速率,反应动力学方程采用了计算电荷传递电流密度 i_{loc,m} 的 Butler-Volmer 表达式(与方程式(3)对比),在三次电流分布情况下表达式还包含了浓度依赖性。
COMSOL 软件中的三次电流分布 接口求解了电解质电位(\phi_l\)、电极电位(\phi_s\)和一组物质浓度 c_i。根据上述假设,可得到以下方程:
电极:\textbf{i}_s = -\sigma_s\nabla\phi_s\ 和 \nabla\cdot\textbf{i}_s = Q_s
电解质:\textbf{i}_l = F\sum_{i=1}^n z_i (-D_i\nabla c_i-z_i u_{m,i} F c_i\nabla \phi_l) 和 \nabla\cdot\textbf{i}_l = Q_l
电解质电中性:\sum_i z_ic_i = 0
电极与电解质界面:\eta_m = \phi_s-\phi_l-E_{eq,m}
典型的电流密度表达式:i_{loc,m} = i_{0,m}\left(\frac{c_\mathrm{Red}}{c_\mathrm{ref}} e^\frac{\alpha_{a,m} F \eta_m}{RT}-\frac{c_\mathrm{Ox}}{c_\mathrm{ref}}e^\frac{-\alpha_{c,m} F \eta_m }{RT}\right)
对于所有参与反应的物质而言,参考浓度 c_\mathrm{ref} 必须是相同的,这确保了过电位在零电流密度(平衡)状态下会遵守热力学 Nernst 方程。
下图展示了线电极示例的三次电流分布情况。由于具有浓度依赖性,三次电流分布会受电解质流动的影响,因此会受到质量传递控制的反应物的影响。当导线之间的流速很小时,为了获得法拉第电流而消耗的电解质不能得到有效补充,从而使电池内的这些部分形成了反应物的耗尽区。这大大降低了局部电流密度,这一现象可描述为“质量传递限制”,它进一步导致更多电流产生于线电极的外边缘。由于电流受到质量传递的限制,因此可以观察到电压降相应地增加,这就是所谓的“浓度过电位”。
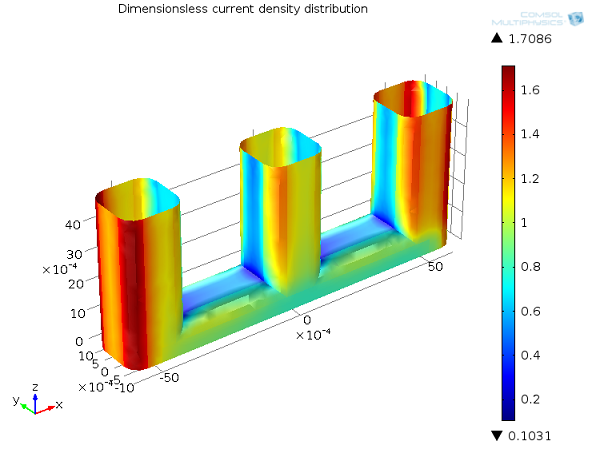
三次电流分布,Ecell = 1.65 V。正极上的电流密度分布(无量纲)。
何时使用三次电流分布 接口?
当电解质混合不均匀或者(与净电流密度相比)浓度相对较低时,可以使用三次电流分布对电池进行模拟,原因是电池内的电解质的组成变化很大,电阻损耗不遵守欧姆定律。在三次电流分布中,利用电流密度和电中性来求解所有 物质浓度的 Nernst-Planck 方程,会使方程组变得非线性和复杂化,致使仿真时间拉长,内存需求增加。在对三次电流分布进行模拟之前,最好利用二次电流分布来预测和判断电化学电池的可能性能。
还有哪些其他选项?
在分析电化学电池的电流-电压关系时,一次、二次和三次电流分布的近似程度依次增加。除此之外,还有其它的建模方法可以最大限度获取有关电池性能的信息,同时尽可能地减少模型的复杂度。
化学物质质量传递和二次电流分布
如果电流密度受到电活性物质质量传递的限制,但电解质组成基本不变,则可能不需要完整求解三次电流分布。相反,离子强度恒定不变意味着我们可以假设电解质溶液服从欧姆定律,具有恒定的电导率,因此可以利用二次电流分布 来求解电解质电位。然而,将动力学速率定律耦合到一个求解化学物质扩散问题的传递模型(必要时也可以求解迁移和对流问题)后,动力学速率定律变得与浓度相关。
事实上,这种耦合方法被用于线电极的三次电流分布案例,这是因为在此案例中是反应物的消耗过程,而非大量电解质物质起到了决定作用。这种耦合方法的另一个应用示例是橙子电池模型。此外,在分析电池和燃料电池时,将电荷传递与质量传递部分耦合是一种普遍的方法。
电分析
当惰性(支持)电解质数量远远超过反应(电活性)物质数量时,就会发生一种特殊情况。因此,与法拉第电流密度相比,溶液的离子强度很大。在这种情况下,电场非常小,因此电解质电位几乎处处相等——电解质溶液电阻对电化学电池的特性没有显著的影响。
当电极动力学(活化)和电活性物质的质量传递的影响远大于电解质溶液电阻的影响时,你可以使用电分析 接口。这个化学物质的传递接口可求解质量传递的对流扩散方程,它包含了电极动力学边界条件,以驱使电极-电解质界面的化学物质通量随局部过电位的变化而变化。
溶液电阻为零的电分析近似适用于电化学技术的标准实验装置,例如循环伏安法、计时安培分析法和电化学阻抗谱。在“案例下载”库中,你可以查看循环伏安法模型的案例,此案例便采用了这种近似方法。
总结思考
本篇博文介绍了 COMSOL Multiphysics 中四个电化学相关模块中都可用的三个电流分布接口,以及何时、为什么要使用它们。COMSOL Multiphysics 软件的强大之处在于,它能够模拟所有电流分布类型(一次、二次和三次),因此在分析电化学电池时,你可以灵活地逐步引入并掌控理论模型的复杂度。
如果你有兴趣使用 COMSOL Multiphysics 来模拟电化学电池设计,或者遇到了本文未提及的问题,请与我们联系。



评论 (24)
WYZFJ
2024-05-19I have a mystery I haven’t figured out. In general, the definition of electrode potential in textbooks or literature is more complex, but it is emphasized that the electrode potential is not equal to the potential difference between the electrode and the solution. However, I found that COMSOL’s definition of electrode potential is this. Does this definition cause the simulation results to be inconsistent with the objective physical facts? Thank you!
chong shi
2024-05-24 COMSOL 员工The electrode potential is the difference in potential between the solid-liquid interface, and it is not directly defined in COMSOL. Generally, only the solid-phase potential is defined, while the liquid-phase potential and lectrode potential are calculated based on interface dynamics and solution properties.
硕 佟
2024-06-24请问二次电流分布+稀物质传递和三次电流分布有什么不同,另外如果电极上电流的分布与溶液电阻相关(电极由一个整流柜供电,整流柜到电极之间还有复杂回路),是不是要手动把电解质电导率写成离子浓度的方程才可以算,有没有其他的方法
chong shi
2024-06-25 COMSOL 员工二次电流分布+稀物质传递等价于“支持电解质-三次电流分布”,从方程形式上两者完全相同,不过前者需要手动做耦合,后者耦合已经自动完成。适用于,电解液电导率对离子浓度变化不敏感的场景,比如加入了大量支持电解质。如果电解质电导率与离子浓度有关,建议采用“电中性-三次电流分布”,它默认考虑电解质离子电导率与浓度有关,确切将与离子通量有关。
荣豪 申
2024-11-19请问直接使用三次电流分布有相关案例视频吗,手动耦合经常报错
chong shi
2024-11-20 COMSOL 员工可以找到很多与腐蚀或电镀相关的,使用三次电流分布的案例,如:https://cn.comsol.com/model/copper-deposition-in-a-trench-2112
Yuan Tao
2024-12-01请问参考交换电流密度以及阴极、阳极传递系数如何设置?我想做阴阳极大小不同的电解水,必须要先进行实验吗,是否有经验值呢?
chong shi
2024-12-03 COMSOL 员工参考交换电流密度以及阴极、阳极传递系数这些参数与电极材料和环境因素(比如温度,电解液浓度等)有关,一般可以通过实验手段获得,比如利用三电极体系测量工作电极的极化曲线或者EIS。电解水的话,阳极反应是析氧,阴极反应是析氢?如果是的话,对应这两个反应的相关参数,也可以从很多文献或者电化学参考书中找到相关参数。
博文 靖
2024-12-24请问参考交换电流密度是否有明确定义?
Ai Haibara
2024-12-13请问三次电流分布物理场水基电中性的模式下H+离子和OH-离子无法参与反应;而支持电解质模式下添加水的自电离平衡反应(顺便问一下单位活性浓度如何填?)无法收敛该如何处理?无法分析中性电解水现象。
chong shi
2024-12-17 COMSOL 员工你好,首先“单位活性浓度”按照默认数值即可,一般取1[mol/L]即1000[mol/m^3]。对应平衡反应而言,因为为了维持浓度平衡,所以一旦局部浓度偏离平衡浓度,会引起较快的反应速率,导致收敛性变差。可以尝试添加“反应”,定义较快的反应速率常数来等效平衡反应。
博文 靖
2024-12-17请问如何在二次电流分布物理场里添加电化学反应的焓变来表述反应的吸热或放热呢?是否需要借助其它物理场引入反应焓?
chong shi
2024-12-17 COMSOL 员工你好,考虑吸热或放热是指要模拟其温度场变化?如果是的话,需要引入“传热”物理场,通过在对应区域施加热源来考虑对温度的影响。而对于电极表面,反应热与反应速率和反应焓有关。
博文 靖
2024-12-17感谢您的回答。我之前已经耦合了“固体和流体传热”物理场,耦合接口中的“电化学热”此时似乎只包含了焦耳热而没有反应热。
在传热场→热源→广义源选项下只包含了二次电流分布物理场预定义的“总功率密度(cd)”选项,其次就是用户自定义功率密度。如果引入“化学”场,则在添加反应后可以直接设置反应的热力学属性(焓变、熵变等),同时上述广义源会多出一个“反应热源(chem)”的预定义选项。
直接指定反应焓变是符合直觉的做法,但我没能在二次电流分布场中找到像化学场那样能指定反应焓值的地方,这是否意味着还需要额外耦合“化学”场来量化电极上电化学反应的吸放热呢?但是化学场中的“反应”似乎没办法限定作用域
yongchao wang
2024-12-20 COMSOL 员工1.多物理场接口”电化学热“是将欧姆热及电化热均考虑在内的,电化学热包含不可逆热和可逆热,可逆热通过定义”平衡电位温度的导数“进行计算,可参考案例:https://cn.comsol.com/model/3d-electrochemical-and-thermal-analysis-of-a-prismatic-lithium-battery-124881
2.如果想从焓变方面考虑可以在”化学“中定义电化学反应方程式,并设定焓变,可以参考案例:https://cn.comsol.com/model/solid-oxide-electrolyzer-using-thermodynamics-74001
博文 靖
2024-12-23好的,感谢您的解答
YAODONG HUO
2025-05-14请问氢燃料电池(fc)模块是否就是二次电流分布模块+化学模块+浓物质传递模块呢?我尝试过用着两种方案去模拟以CO和H2为燃料的SOFC,发现这两种方案模拟出来的结果不一样。氢燃料电池(fc)模块的结果是正常的,而二次电流分布模块+化学模块+浓物质传递模块方案中,CO的摩尔分数变化趋势是增加的,导出内部方程发现第一种方案CO的过电位全为正数,而第二种方案CO的电极过电位有负数的情况出现(靠近电解质那一侧为正数,远离电解质侧为负数),导致CO的电流密度有负数的情况出现,请问出现这种情况的原因是什么呢,两种方案的本质差别是什么呢?谢谢!
yongchao wang
2025-05-14 COMSOL 员工1.燃料电池接口可以使用二次电流分布+化学+浓物质传递手动耦合进行替代,还要耦合相关的流场接口进行建模,如果耦合及参数设置合理一般计算结果基本相同,对于你提到的模型问题,建议将模型上传到技术支持,这样可以根据模型进行针对性的解答;
2.可以参考官网SOEC的两种建模方式自行修改模型,模型链接:https://cn.comsol.com/model/solid-oxide-electrolyzer-using-thermodynamics-74001
DUI HAO
2025-05-28您好,我想请教两个问题:
1.在三次电流密度分布中,支持电解质、电中性、泊松三个选项有什么区别呢?我发现在电解质区域的方程式图中,泊松选项是没有算电解质电导率的方程的,而其他两个就有,是否意味着选泊松就无法算电解质电导率呢?
2.第二个问题是,我发现案例都是使用三次电流分布去计算电解质中离子的浓度,三次电流分布是否能用于计算固体电解质中,电子和缺陷的浓度分布呢?谢谢!
Yi Li
2025-06-06 COMSOL 员工1、支持电解质:假设电解质中存在大量惰性“支持电解质”(如高浓度的盐),其离子迁移主导电荷传输,因此电解质中的电势梯度极小,使用体积电导率来定义电解质电位降;电中性:假设溶液中任意位置净电荷为零,直接通过电中性条件求解电势分布;泊松:不假设电中性,通过泊松方程求解电势分布,需要完全解析双电层,一般适用纳米尺度问题,不包含显式的电解质电导率
2、三次电流分布接口的适用范围主要是电解质中带电物质(离子)的传递、电荷转移反应动力学和物种传输(如扩散、迁移和对流),您提到的电子和缺陷应该并不适用
Shang Nalan
2025-08-05COMSOL员工,您好,在“线电极”案例中看到了“反应流,稀物质”和“电位耦合”的多物理场接口,最近在做液流电池仿真,我想请问如何将三次电流分布物理场与自由和多孔介质流动物理场进行耦合,以进行电场、流场和浓度场的后处理,请问案例库有没有类似模型,谢谢?
yongchao wang
2025-08-05 COMSOL 员工二次电流+稀物质传递的耦合等价于三次电流分布的支持电解质的电荷模型,三次电流分布与自由和多孔介质流动耦合可参考案例(案例中流场使用的是Brinkamn方程,设置与自由和多孔介质流动完全一致):https://cn.comsol.com/model/capacitive-deionization-of-saline-water-126701
Cheuksing Lam
2025-08-30您好!请问三次电流分布(TCD)是否支持气体生成呢?例如,一个阴极为析氢反应的电解池,对阴极域使用TCD,软件仍要求输入氢气的溶液扩散系数等。但如果我想模拟氢气完全不溶于水的情况,应如何设置?能否耦合“气泡流层流”模块?若能,如何“使TCP模块知道生成的是气体,并将此部分交给气泡流模块处理”?注:阳极为纯离子反应,因此不能对整个电解池使用“电解水模块”。谢谢!
yongchao wang
2025-09-02 COMSOL 员工三次电流分布与气泡流进行耦合可以参考案例《使用气泡流建立铜电解沉积两相流模型》:https://cn.comsol.com/model/two-phase-flow-modeling-of-copper-electrowinning-using-bubbly-flow-75111