利用形状优化来设计新结构

设计新的结构时，你是否曾经对如何获得最优形状感到迷茫？如果是这样，那么你一定会乐意学习一种非常有用的称为“形状优化”的技术，拥有了这项技术，你的 COMSOL Multiphysics 建模技能就又提高了一步。今天我们将探讨形状优化的概念，并借助一个典型案例来演示其用法。

形状优化的背景

工程师、研究人员和科研人员们一直在努力改进设计。优化是指这样一种理念，即改变零件尺寸和材料属性等模型输入数据，实现某些指标的提升，同时还满足一组约束条件。COMSOL Multiphysics 中的优化模块是处理此类问题的得力工具。

尺寸优化是其中一种比较常见的优化技巧。这个方法要求直接更改 CAD 尺寸，实现质量最小化，可参考我们的支架的优化教程。在这个支架示例中，我们利用所谓的无梯度技术调整尺寸，同时还考虑了以下约束：尺寸间关系、峰值应力以及最低固有特征频率。这些技术会根据不同的目标函数和约束类型采用不同的处理方法，因此相当灵活。不过，这些技术有一个缺点：必须不断地对零件重新剖分网格，从而使设计变量从数值上逼近目标函数和约束的灵敏度。

如我们在以前的一篇博客文章中讨论的，在使用变形几何接口时，如果几何发生变化，那么也可以通过分析计算设计灵敏度。进一步来讲，基于梯度的求解器无需重新剖分网格，即利用灵敏度优化零件的尺寸，这是我们在设计电容器一文中重点讨论的内容。回顾以上两篇博客文章有助于理解我们今天要使用的功能。

形状优化是对以前讨论的相关概念的一个延伸，其中不仅考虑了简单的尺寸更改，还涉及到形状的总体改变。结构的形状受控于一组设计参数，这些参数使用了一组能描述任意形状的基函数。在下文中，我们将结合具体案例进行探讨。

形状优化问题：梁的厚度

调整悬臂梁的厚度是一个典型的形状优化问题，我们以此入手来进行探讨：调整悬臂厚度并使其质量最小化，同时满足自由端上挠度峰值的约束。梁的初始厚度均匀，但顶部表面上分布的载荷不均匀，请参考下图。

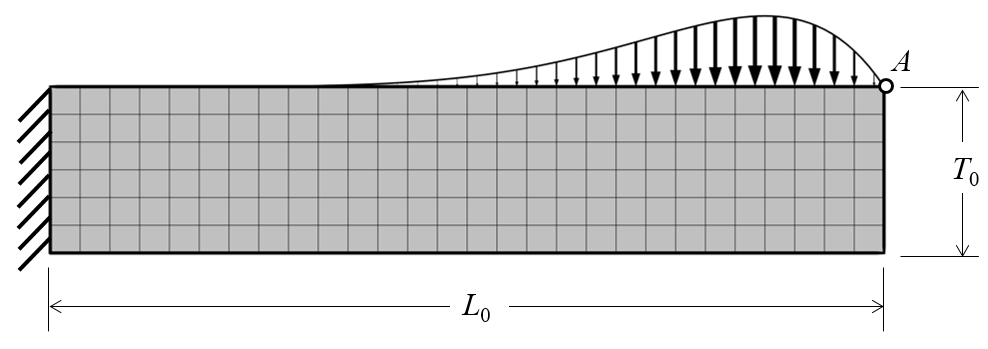
载荷不均匀的悬臂梁，点 A 的挠度不应超过指定值。图中还显示了网格。

我们先选择设计变量。在悬臂端，梁的长度和厚度固定，长度方向上梁的厚度可以改变。根据初始配置改变厚度会稍微更简单些。不过，我们引入了函数 DT(X)，它在长度方向上的初始值为零。

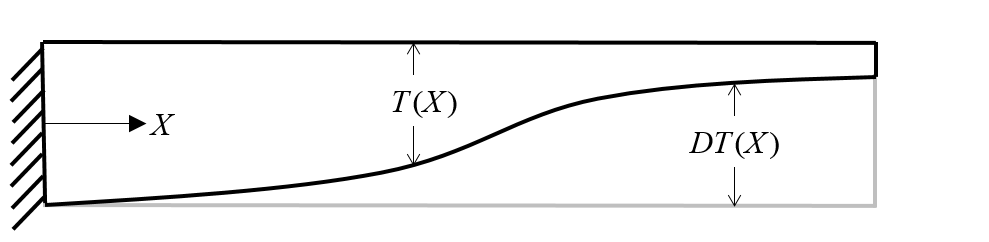
优化问题研究梁的厚度变化。

在这里，我们选择用一组四阶伯恩斯坦多项式表示厚度变化：

用归一化尺寸表示：\bar X = X/L_0。请注意，此函数已按比例缩小了，这样多项式系数的数量级接近 1。这样做也是为了实现缩放的目的。

因为 X=0 时梁的厚度已指定，因此在固定 C_0=0 时，DT(\bar X)=0，所以这一项可略去。在远端，我们添加了一个约束条件：梁不能太薄，即 C_4<0.9。

至于中间区域，我们也希望添加一些约束，进一步限制设计空间。可以添加约束 0 < DT(\bar X) < 0.9T0。不过，这一约束有个缺陷：梁的厚度会忽薄忽厚。但是根据基本原理，我们知道这种情况不合常理，在长度方向增加梁的厚度毫无益处。我们就对其导数添加约束：DT^\prime(\bar X) > 0。这个约束迫使梁的厚度沿长度单调增加，随之还带来的好处是很自然地满足了约束条件：0 < DT(\bar X) < 0.9T0。

还要考虑另一个约束：梁一端上点的位移。我们希望点 A 的位移量不超过指定值 u_{max}。根据以上信息，我们现在的优化问题就比较完整了：

这里，目标函数针对梁的初始质量 M_0 所作的归一化已完成，目标函数已缩放，其阶次为 1。类似地，梁端部的位移量 |\mathbf{u}_A| 针对容许的最大位移 u_{max} 进行归一化，它应当小于 1。现在我们来看一看如何在 COMSOL Multiphysics 中使用“优化模块”实现此类问题。

在 COMSOL Multiphysics 中实现这个问题

我们先从初步设计开始，即一个长度固定、厚度均匀的梁。梁一端设计为悬臂式，顶部表面的载荷不均匀，其变化遵循 \bar X^4(1-\bar X )。我们希望先引入厚度变化的函数。之前描述的多项式函数是变量 DT，如下方截图所示。表达式 Xg 指最初未变形几何的 x 维度。此函数在归一化的 x 方向上的导数是变量 dDTdX。两个全局参数 L0 和 T0 定义长度和最大厚度。

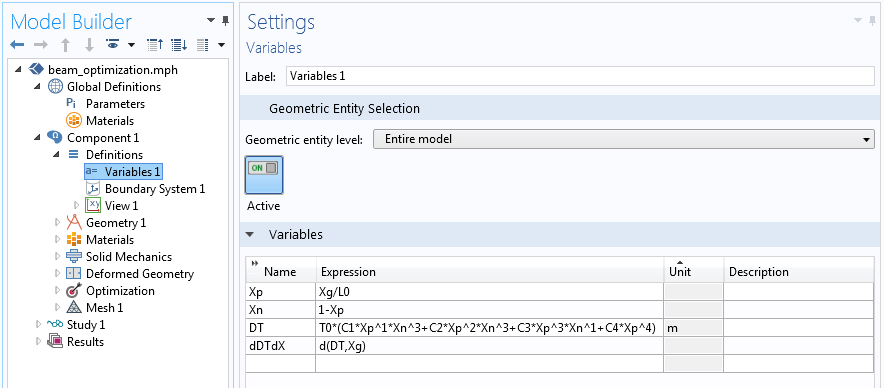
屏幕截图显示厚度变化的函数及其导数。

有关厚度变化的变量用在变形几何接口中，定义梁的总体积如何随厚度变化而变化。因为只有厚度变化，所以可以使用简单的线性映射，如下图所示。

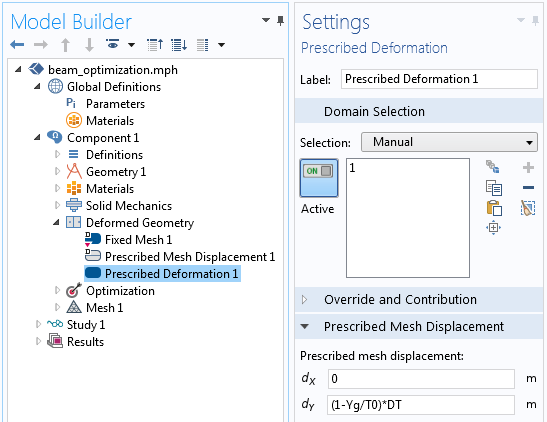
梁内的位移就指定完毕。

现在通过优化接口建立优化问题，其中可以很轻松地创建比较复杂的含多个约束的优化问题。相关设置显示在下方的屏幕截图中，先设置目标函数。积分目标特征对材料密度在建模域进行积分，并针对初始零件质量进行归一化。

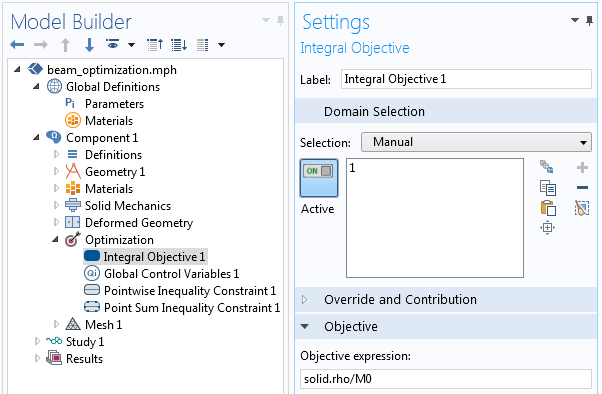
优化的目标是质量最小化。

全局控制变量特征的设置如下所示。四个变量 C1、C2、C3 和 C4 的初始值为零，相当于梁的初始形状。对 C4 的约束是施加了一个上界，所有变量的缩放比例均为 1。

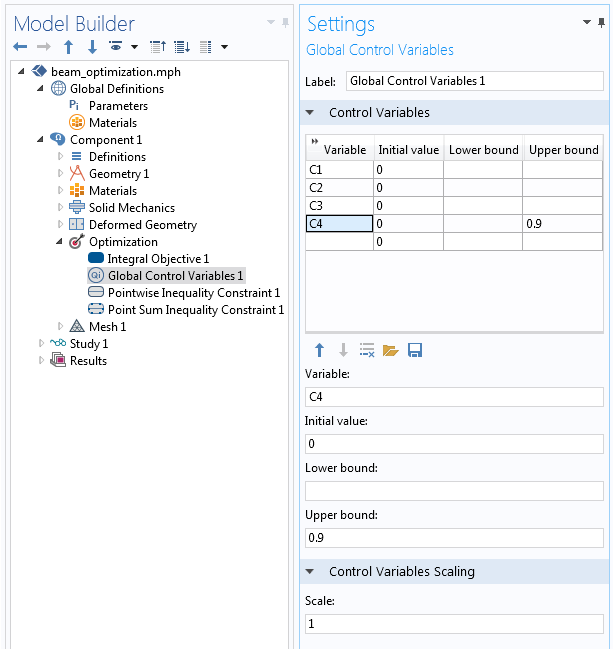
控制变量及其界限和缩放比例的定义。

接着，将逐点不等式约束特征施加到域的底部边界。该特征强制每一点的位移函数的导数均为正，从而确保函数单调增加。

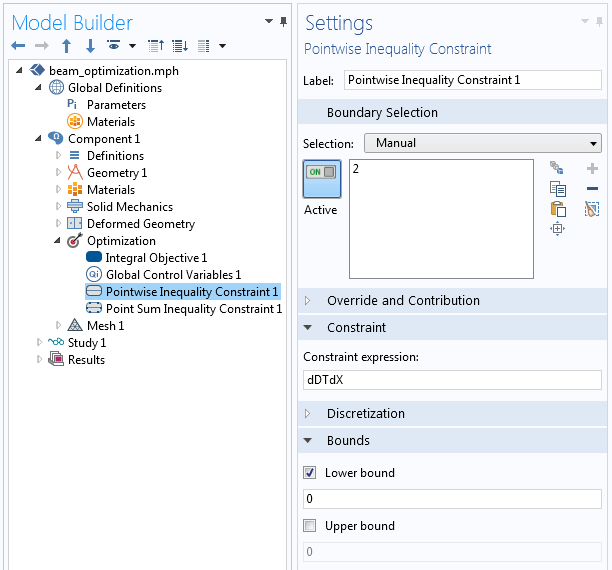
通过逐点不等式约束对沿梁长度的导数施加约束。

最后，对梁远端点的峰值位移施加约束，使其小于最大指定值。可通过点求和不等式约束特征设置该值。

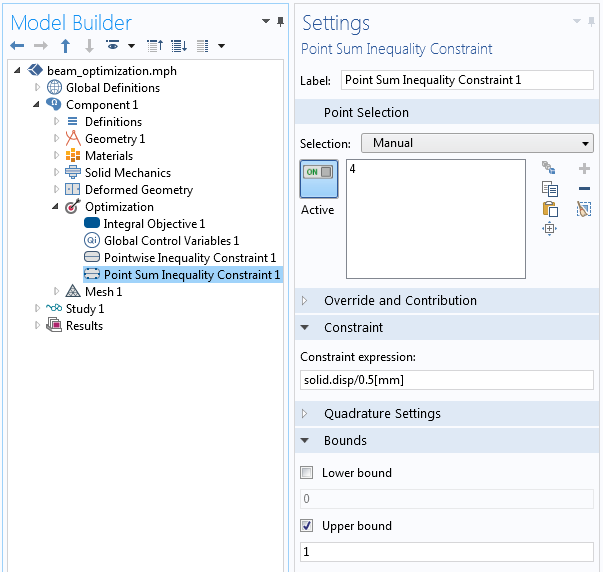
对归一化的峰值位移施加约束。

至此，我们的优化问题基本创建完毕。最后一步是将优化特征添加到研究序列，选择基于梯度的 SNOPT 求解器，经证实该求解器能最快速地处理我们的问题。所有其他设置保留默认值。目标函数和约束自动取自优化接口。

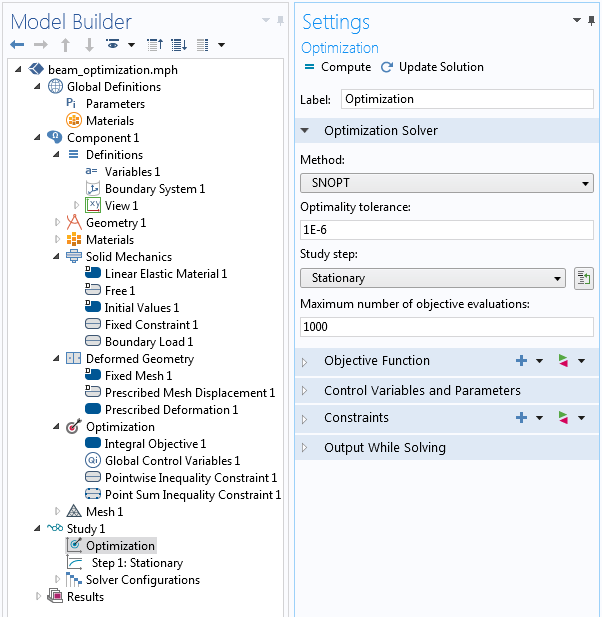
相关的优化求解器设置。

下图绘制了结果。其中已显示根据上述步骤得到的最优形状。端部的位移最大，厚度沿长度单调增加。我们预计几何会变形，因此使用了映射网格。

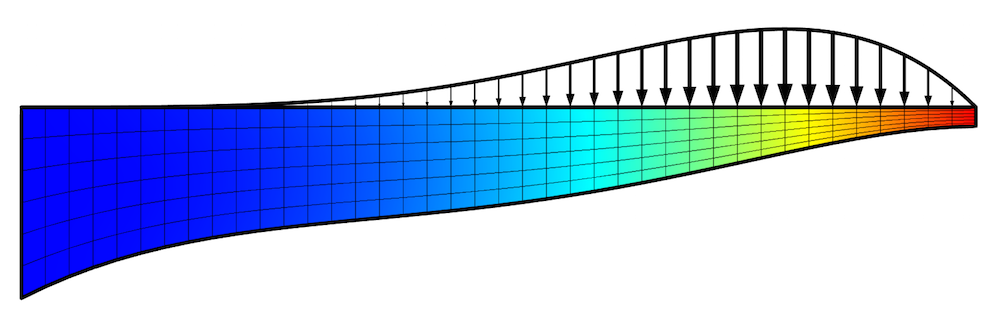
优化后梁的形状，施加不均匀载荷和约束后实现了质量最小化。其中绘制了位移场，以及施加的载荷分布和网格。

使用形状优化设计新结构的总结

或许我们自己会疑惑，如何能确定以上的结构真正实现了最优化。因此我们强烈建议进行网格细化研究，尝试不断细化网格，以了解其解如何收敛。研究基函数的收敛性也是非常合理的做法。我们可以使用高阶伯恩斯坦基函数并比较结果。不过，这样做可能会导致龙格现象，还会使收敛缓慢。

将原区间细分为多个子区间，在每个子区间（分段多项式）使用不同的较低阶形函数，可规避此类问题。除了伯恩斯坦基函数外，我们还可以应用其他基函数，如切比雪夫多项式和傅立叶基函数。号角优化形状教程重点讨论了使用傅立叶基函数的案例，该教程可从“案例下载”中下载。

本篇博客文章讨论的案例中，所包含的变形十分简单。在涉及更复杂的变形时，需要花更多心思考虑如何定义变形映射。在计算非常复杂的变形时，添加辅助方程也会很有帮助。
如果你对使用这些形状优化技术有任何疑问，或者希望将优化模块加到自己的建模工具套件中，请联系我们。