AC/DC 模块最常见的用途之一是模拟电磁线圈及其与周围环境的相互作用。今天,我们将研究在对线圈进行建模时需要牢记的一个关键概念:闭合电流回路。如果你的工作涉及线圈建模,通过这篇文章,你将对这个主题有一个全面的了解。
如何在 COMSOL Multiphysics 中模拟基本线圈
让我们从一个简单的导线示例开始。如下图所示,一根导线弯曲成一个环并连接到一个恒定的电压源——电池。由于存在电压差,电流将通过导线流动。整个导体的电流大小和方向可以通过欧姆定律和电荷守恒方程以及一组边界条件来计算。

连接到直流电压源的一个非常简单的电磁线圈。
对于这根单匝线圈,我们可以考虑一端接地的边界条件,即电势为零,而另一端的电势较高。电流不能在其他地方流入或流出导线,所以电绝缘条件适用于其余的边界。这个问题可以用 COMSOL Multiphysics AC/DC 模块中应用的有限元方法来解决。
由于计算出的电流流动,产生了一个围绕导线的磁场。这是一个向量场,具有大小和方向,可以通过安培定律计算。我们感兴趣的是学习如何模拟这个磁场,以及它如何与其他物体相互作用。
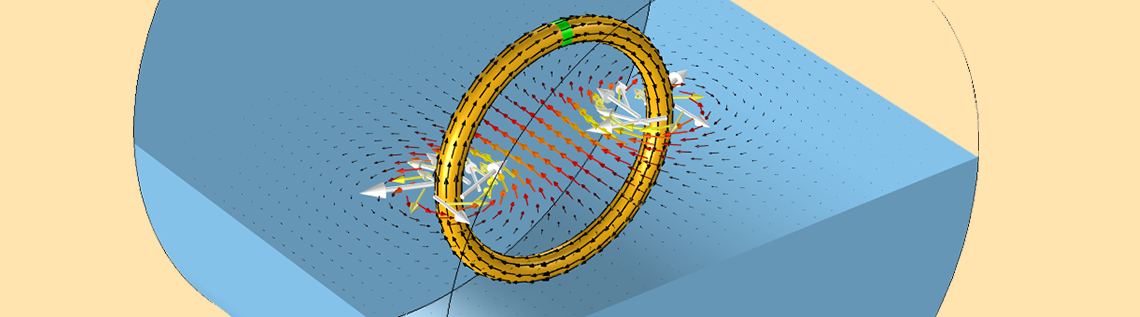
由于我们的目标是学习线圈建模,所以不会关注源本身发生了什么。我们将假设存在一个提供恒定电压或恒定电流的设备。我们也不关心线圈和源之间的电线,而是假设它们在电气上无关紧要。基于这两个假设,我们认为,一个合理的线圈计算模型可能看起来像下图所示的模型,该图显示了单匝线圈以及由于电流流动而产生的周围磁场。

单匝线圈的计算模型。导线中的电流(黑色箭头)会在周围空气域产生磁场(彩色箭头)。
实际上,在解决上述模型的过程中,还有一些其他的假设。首先,我们可以看到,线圈周围有一个圆柱体,代表空气域。这是我们求解磁场的计算域。这是一个有限域,但磁场实际上将无限延伸到离线圈很远的地方。磁场强度将随着与直线距离的倒数而下降,因此在离线圈很远的地方,磁场将非常小。虽然它永远不会精确为零,但我们可以合理地将我们的建模域截断为一个有限的空间。
通过在线圈周围选择一个有限的建模域,我们假设只对这个区域的场感兴趣。选择有限域在边界处引入了另一个假设。我们需要考虑沿着圆柱体或选择的任何周围区域形状的边界的一些边界条件。我们将在之后的博客中详细讨论各种可能的边界条件、它们的物理解释,以及为什么要使用每一个边界条件,但对于这个特定的案例,我们将考虑一个代表完美电导体的边界条件。
对于此的物理解释,我们假设线圈位于圆柱形金属容器内。而这个边界条件产生结果是,沿导线从一端流向另一端的电流将沿建模域的表面流回,如下图所示。
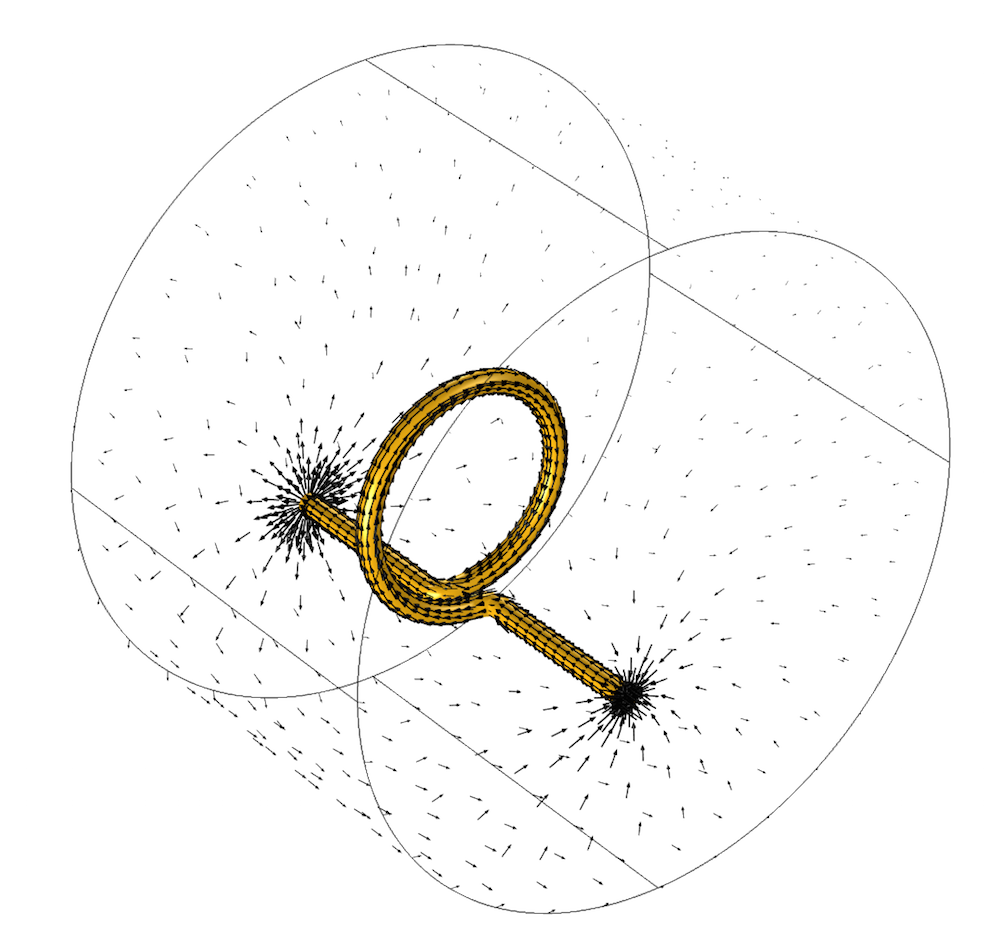
箭头显示流过导线并沿截断建模域的表面返回的电流。
这让我们看到了线圈建模中最基本的一点:闭合电流路径的概念。
一个重要的建模条件:闭合电流路径
每当为一个线圈或任何由电流激发的磁场建模时,都必须有一个封闭的电流路径(回路)。你建立的模型必须满足这个条件才有效。如果你试图施加一个流经开路线圈的电流,相当于暗示电流(电子)瞬间从开路线圈的一端移动到另一端,这将违反麦克斯韦方程。下面的图片说明了这样一种无效的线圈模型。由于线圈的导线没有延伸到边界,所以没有连续的路径,电流可以沿着它流动。

无效的线圈模型。载流导线没有到达边界,因此电流无法环回,没有电流可以流动。
闭合模型中的当前路径
通过重新审视一些假设,我们可以对线圈模型采取另一种方法。在上面的例子中,我们所做的一个假设是,源在建模域之外。然而,我们可以改变我们的模型,使源位于建模空间内。
下图展示了这样一个代表性模型。图中显示了一个闭合线圈,其中一个小区域代表给线圈供电的源。这个源(在下图中以绿色显示)完全在建模域内,并闭合了当前路径。我们还假设馈入线圈的导线对于建模需求并不重要,并且假设闭合的环是线圈的合理近似值。
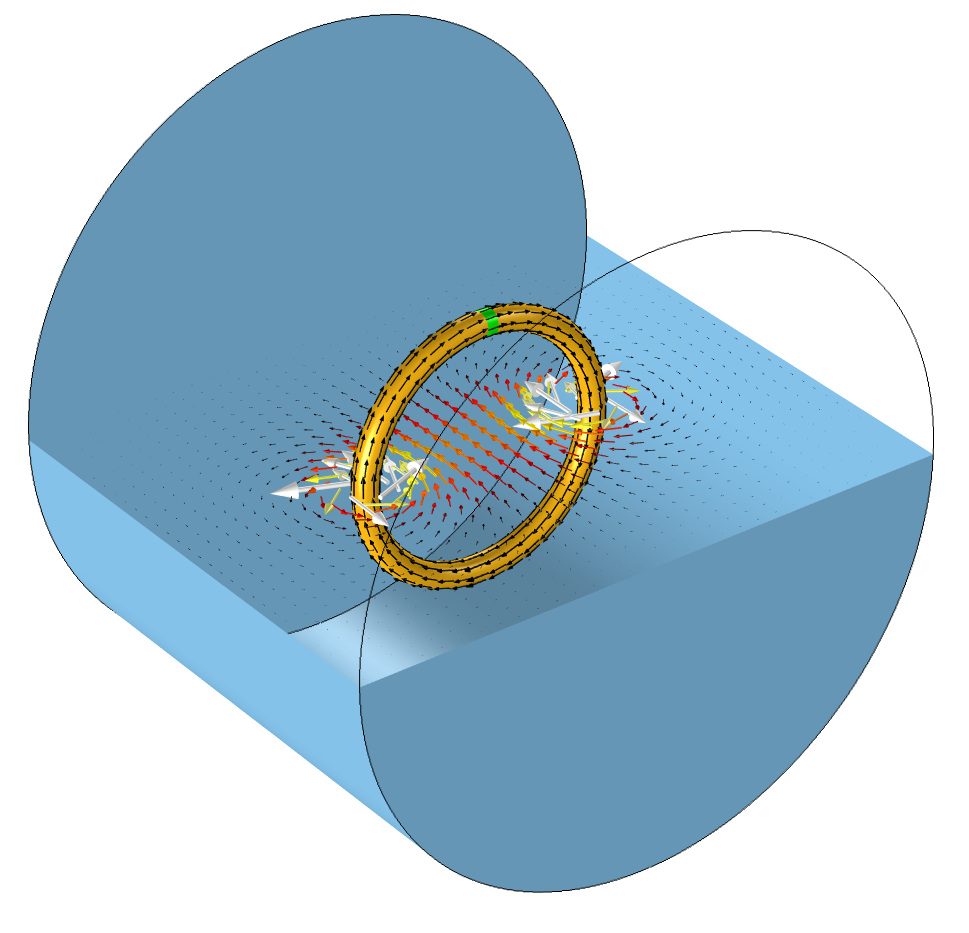
一个线圈模型,它的源位于建模域内。源是绿色的一小部分。线圈具有完全在建模域内的电流返回路径。导线中的电流(黑色箭头)会在周围空气域产生磁场(彩色箭头)。
使用这种方法建模还有一个有趣的结果,就是建模域的边界不再需要提供一个电流返回路径。这就为建模域外部的替代边界条件提供了可能性,它可以用来模拟一个绝缘的周围环境,或者近似于一个无限的空间,而不是一个封闭的导电容器。我们将在后文中深入讨论截断建模域的各种适当方法。
二维和轴对称模型中的电流路径
对于二维和轴对称模型,我们还需要关注当前的返回路径,所以让我们快速了解一下在这些情况下的有效配置。当要解决的磁场围绕旋转轴不变或几乎不变时,适合使用轴对称模型。下图中的示例就是一个这样的三维几何图形,以及相关的轴对称二维模型。假设所有场围绕对称轴是不变的,公式本身默认闭合当前路径,因此我们只需要在正 rz 平面中建立一个二维域的模型。
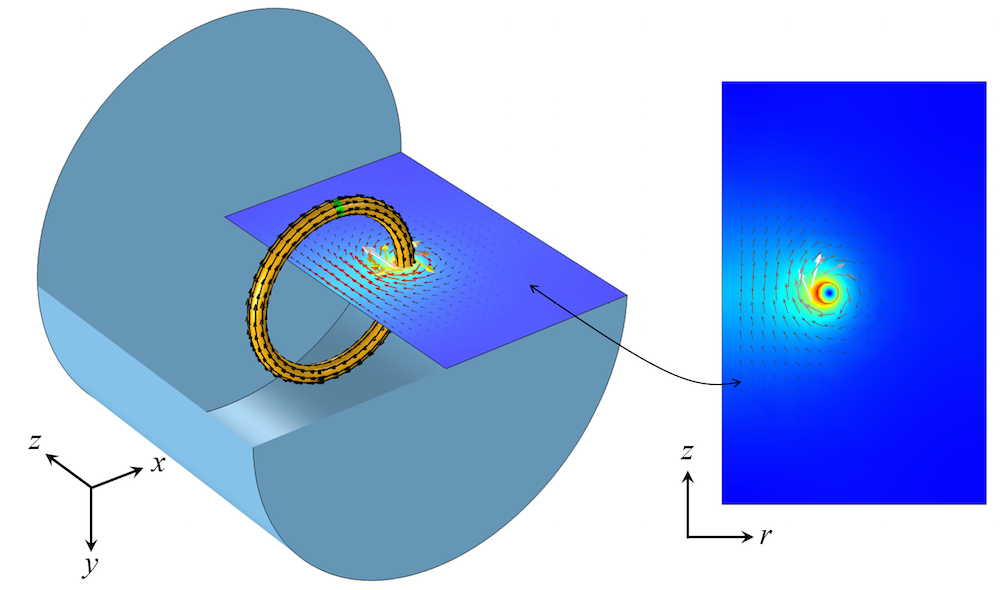
一个在三维旋转方向各变量保持一致变化的线圈,可以在轴对称的二维平面中建模。
如果线圈非常细长,那么末端效应可以忽略不计,就像在电机中看到的那些,也有可能将模型减少到一个简化的二维模型。有两种不同的选择来闭合电流路径。我们可以对整个线圈的横截面进行建模,导线以相反的方向携带电流,或者只对线圈的一半进行建模,并在中心线上设置对称性条件。
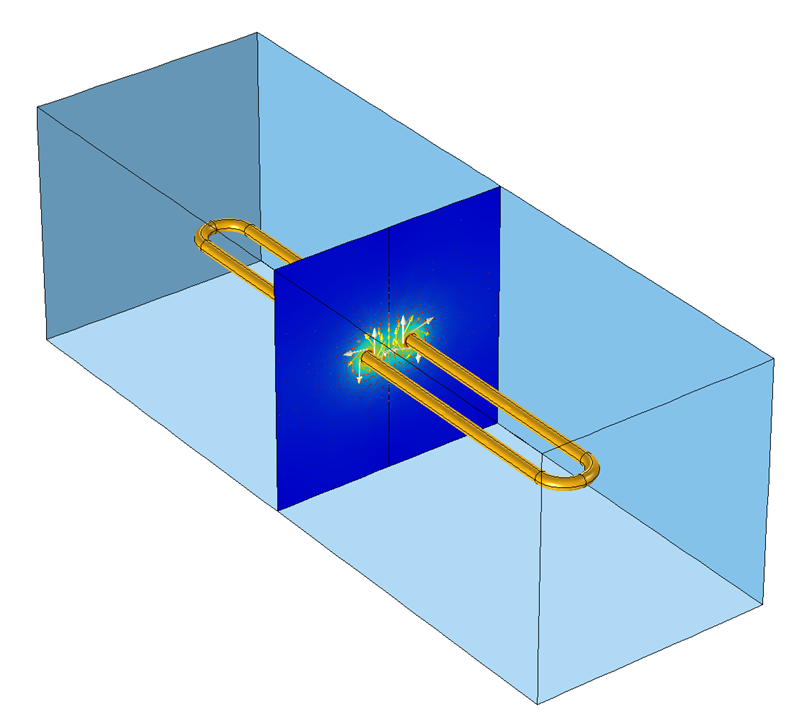
一个细长的三维线圈模型。如果忽略末端效应,可以在二维平面中对其进行建模。
当对两匝线圈进行建模时,一匝将电流垂直传送到二维建模平面,另一匝则将电流垂直传送出二维建模平面。当仅对单匝进行建模时,必须在中心线处使用对称条件,以允许电流沿相反方向回流。二维建模平面的边界闭合了当前路径。这两种情况如下图所示。
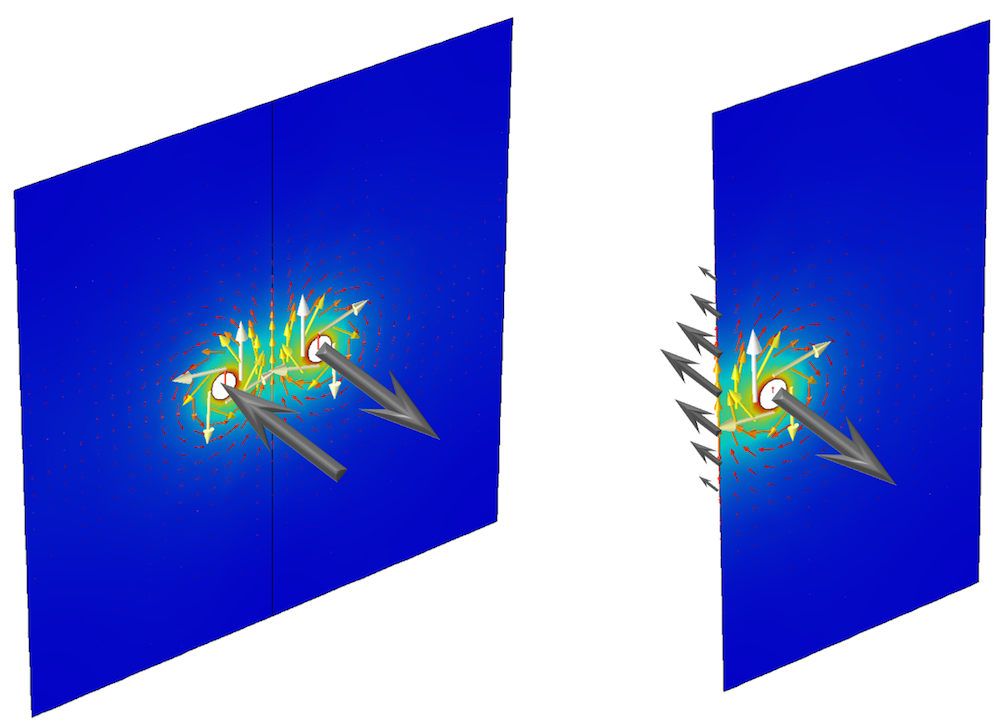
在二维平面中对细长线圈进行建模的两种不同方法。沿正负平面外方向(灰色箭头)流动的电流沿线圈或对称边界条件流动。
关于使用 AC/DC 模块进行线圈建模的总结性思考
我们以介绍电流闭环的概念开始,研究线圈的建模。如果你正在为一个线圈建模,或者确实在做几乎任何与电流和由此产生的磁场有关的建模工作,那么你应始终需要记住这个概念。下一个我们将讨论的主题是计算模型的适当边界条件问题,敬请继续关注。同时,你还可以查看以下这些学习资源。
- 在 COMSOL 博客上阅读有关如何使用 AC/DC 模块的更多信息。
- 在三分钟内了解如何使用 AC/DC 模块对计算电磁学进行建模。观看视频。
- 如果你想使用 COMSOL Multiphysics 和 AC/DC 模块进行线圈建模,请联系我们。



评论 (1)
科铭 黄
2022-09-01闭合模型中的当前路径这部分,三维单导体线圈不能施加电流激励吧。