最新内容

使用 COMSOL 理解稳定性方法
在这里,我们提供了一个质量传输示例模型,以帮助描述稳定方法对您的数值模型的影响。

变形固体中的传热仿真
在之前的文章中,我们介绍了一些涉及静止固体耦合传热的应用。这些静止固体传热示例对将要求解的传热方程进行了简化处理,并且通常可以得到求解温度场的精确近似。当涉及传热和固体力学的多物理场耦合时,如何描述用于解释材料热弹性效应的相关物理场?

地热能:利用地热实现冬暖夏凉
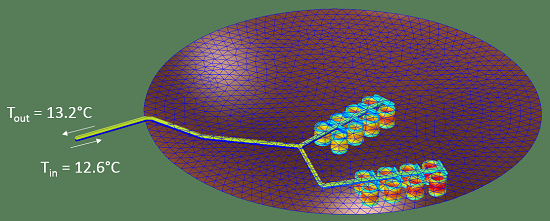
利用地热调节室内温度具有成本低、可持续使用的特点。本文为地热能系列的第三篇博客文章,我们将详细探讨埋管集热器。由于对埋管集热器的热性能已做了准确预测,并且考虑了管道布置与局部热性质,因此“管道流模块”非常适合模拟这种集热器。

射频加热和微波加热模拟快速入门
在射频加热和微波加热网络研讨会中我们经常演示波导模型,因为使用它阐述概念人们比较容易理解。这里,我们再次将其作为模拟射频加热和微波加热的快速入门。

非线性材料的热疲劳建模
在模拟非线性材料的疲劳时,有两个挑战。1.) 正确地表示材料的行为;2.)找到一个能够捕捉到寿命控制机制的疲劳模型。
如何在不知道积分限的情况下对函数进行积分?
您知道 COMSOL® 软件可以解决积分和偏微分方程吗?学习如何积分函数——即使不知道积分的极限。

弱形式的力量
如果你正在使用有限元仿真软件(例如 COMSOL Multiphysics),就会在某些时候遇到“弱形式”这一表述。这个时候,你可能会想知道这个表达是什么意思?实际上,弱形式是一个非常强大的概念。

传热与地下多孔介质流的耦合仿真
本文为地热能系列博客的第二篇,将重点探讨传热与地下水流耦合的过程,并据此确定地下储藏的热量是否足够多,以及是否值得开采获得地热能。文中,我们将通过一个地下水换热回灌系统示例模型演示这一耦合过程。

在 COMSOL Multiphysics® 模型中使用 MATLAB® 函数
您知道可以在 COMSOL Multiphysics® 模型中使用 MATLAB® 函数吗?我们将在本视频教程中向您展示如何通过 LiveLink™ for MATLAB® 实现这一功能。

COMSOL Multiphysics® 的几何内核
几何内核 是负责处理 COMSOL Multiphysics® 中几何的软件组件。您或许想要了解它的意义、原理及作用。我们将在下文中进行介绍。

COMSOL Multiphysics 能够求解什么类型的流-固耦合问题?
经常有人问我:“COMSOL Multiphysics 能够求解流-固耦合(FSI)问题吗?”答案当然是肯定的。接下来,我将介绍几种求解流-固耦合问题的方法,以及分析这些不同问题所需要的 COMSOL 产品。 各种类型的流-固耦合模拟 广义上讲,只要模拟过程涉及计算流体中的速度和(或)压力场,以及与流体相互作用的固体材料中的应力和应变,就是在求解流-固耦合(FSI)模型。 圆柱绕流 在模拟流-固耦合问题时,您可以进行各种假设,来降低模拟的复杂度并减小计算量。首先,我们来看一个使用 COMSOL Multiphysics 创建的最完整的流-固耦合模型:绕圆柱的流体流动。 切向流场中一个圆柱体尾流中的柔性物体变形情况。 圆柱体后方的流体尾流引起其后方的突出物产生大幅振荡,求解这类模型需要解决三个问题。首先,在流体流动区域求解纳维-斯托克斯方程。接着,计算固体位移。最后,求解流动域的网格变形问题,以考虑流体可以流经的变形区域。 对于这种非线性多物理场耦合,您可以使用 MEMS 模块 或者结构力学模块中的流-固耦合 接口模拟。这类模拟可以在时域中求解,也可以看作稳态(定常)问题求解。 上述示例考虑了固体材料中应力和应变之间的线性关系。如果想模拟具有非线性应力-应变关系的材料,例如通常用于描述橡胶和聚合物的超弹性材料模型,还需要使用非线性结构材料模块。 蠕动泵:一种利用滚轮在软管上滚动来推动流体流动的泵。 图片来源:Veryst Engineering。 单向流-固耦合 另一种情况,您可能提前知道结构位移相对较小,但应力可能很大。对于这种情况,仍然可以使用 流-固耦合 接口,但也可以使用 单向耦合 求解器计算流动解,并在结构上施加流体载荷。这样,就可以避免计算网格的变形。 您也可以完全不使用流-固耦合接口,重新开始考虑这类单向耦合 FSI 问题,铝挤出工艺中的流-固耦合案例模型就介绍了这种处理方法。此外,如果您正在求解非常高速的流动问题,并且不关心流动中的短时间尺度紊乱振荡,那么可以将湍流流动模型作为流-固耦合模型的一部分。CFD 模块和传热模块中都包含适用于不同流态的各种湍流模型。 周期性流场中的太阳能电池板模型:计算了太阳能电池板周围的湍流气流和由此产生的结构应力。 流体中的结构振动 如果您提前知道正在模拟的是流体中的振动结构,那么通常可以假设结构位移相对较小。因此,在周围流体中诱发的任何体运动都可以忽略。但是,由于结构在振动,流体将产生压力波,从而产生声辐射。我们可以通过 COMSOL 软件中的声学模块所提供的 声-结构相互作用 接口来求解这类问题。 这个接口假定物体位移的变化相对较小,因此不会引起流体产生明显的体运动,只会引起流体压力场的变化。您可以在时域中求解这类问题,也可以假设位移和压力随时间呈正弦变化。这样,就能够在频域中模拟,耗费较小的计算量。在模拟分析过程中,还可以考虑包括由于流体黏度和材料阻尼引起的体损耗。 扬声器辐射的声压级。 此外,您还可以进一步求解热热声-固耦合问题,它求解的是纳维-斯托克斯方程的线性频域形式,还可以考虑显式模拟产生的热和黏性边界层中的损耗。虽然这比声-固耦合问题的计算成本更高,但仍然比求解完整的流固耦合问题更高效。 振动微镜: 振动微镜的应力和位移以及周围空气的速度分布。 多孔弹性介质 声学模块中的 多孔弹性波 接口还可以模拟波在多孔介质(如潮湿的土壤、生物组织和减震泡沫等)中的传播。这个接口可以同时求解结构位移和固体孔隙中流体的压力。例如,计算声波在水-沉积物界面的声反射。 如果您对模拟多孔弹性介质感兴趣,但需要在稳态或时域而不是在频域中求解,那么你需要使用地下水流模块。该模块可以模拟土壤和其他多孔介质中稳态或瞬态压力驱动的流动和静应力。它还包含一个 多孔弹性 接口,用于模拟稳态和瞬态状态下多孔弹性流体和结构的相互作用。 开孔分支井模型: 绘制了土壤中的应力和多孔弹性域中的流体速度。 薄层流体和管道流 上述所有方法都显明确模拟了流体的体积,并求解了这些体积中的速度和(或)压力。在流体层相对较薄的情况下(例如在流体动力轴承中),完全可以不采用整个流体的体积模型,而只求解雷诺方程,获得流体薄膜中的压力。 这种方法只求解沿域边界的流体流动。CFD 模块和MEMS 模块都内置了这个接口。您甚至可以更进一步,只求解沿一条线的流体流动。换句话说,可以使用管道流模块求解沿管道的流动。 对于同时考虑求解沿管道长度的压力变化和管壁弹性影响的模型,请查看这个求解水锤方程的案例模型。 可倾瓦推力轴承:润滑层中的压力场和可倾瓦推力轴承的变形。 进一步简化计算 您可能已经发现,我们是从最复杂的示例开始,逐步探讨如何简化计算,尤其是流体流场的计算。现在,考虑一种极端的情况,即流体完全不移动但确实对结构施加了一个静水压力载荷的示例。 核心功能 对于这种情况,我们可以利用 COMSOL Multiphysics 的核心功能:用户自定义方程、组件耦合算子和全局方程来解决。这些功能允许在模型中引入任意方程,来表示如流体压力等任何变量。正如我们在上一篇博客中所介绍的,您也可以在变形的封闭腔中考虑可压缩和不可压缩流体的影响,以及由此产生的静水压力。 搅拌器模块 我们已经介绍了简化流体流动问题和计算应力的各种方法,接下来,我们考虑已知固体刚体运动的情况下,如何模拟流体运动。对于这种问题,我们可以通过搅拌器模块来求解,即求解搅拌器和搅拌容器的问题。 在这些问题中,固体结构的运动完全由旋转定义,然后再计算流体的运动情况。如果假设固体发生线性弹性变形,还可以计算运动固体中的应力分布。这可以通过单向耦合来解决,即先求解由搅拌器搅拌引起的流体流动,然后在结构变形较小的假设下计算应力。 搅拌器中的流场。 结语 如您所见,COMSOL Multiphysics 能够处理各种类型的流-固耦合模拟问题。如果您对文中的内容感兴趣,或者文中介绍的内容没有涉及您所关注的问题,请联系我们。

建立贝奥武夫集群加速多物理场仿真
很多人都需要最新的软件和硬件来提升工作效率,因此,我们要紧跟科技发展的步伐。但如何处理过时的硬件呢?将它们报废或是扔在角落,这都显得有点浪费。其实我们可以利用这些废旧硬件来组建一个贝奥武夫集群,以提升计算速度与生产率。
使用 COMSOL Multiphysics 估算化学反应参数
化学反应动力学系列的最后两篇博客文章关注基于一组特定参数的化学反应的建模。尽管这一点很重要,学术界和工业界对此也很感兴趣,但通常在建模时,会假设相关参数的取值。

可变形容器中流体的静水压力建模
在之前的一篇博客文章中,我们研究了计算和控制充满不可压缩流体的腔体的体积,其中求解了充满流体的橡胶密封件的静态变形。在那个例子中,假设流体是不可压缩的,我们没有显式地为流体建模,而是添加了一个方程来求解压力。在这篇博客中,我们将扩展这种方法并使之包括可变形容器中流体的静水压力。 挤压水气球 考虑一个装满水的橡胶气球,放在一个开着洞的表面上,同时被压头从顶部推动。气球的变形是由于流体的重量以及压头从顶部向下推动造成的,如下图所示。我们采用超弹性材料模型对橡胶材料进行建模,并将使用在前一篇文章中介绍的技巧,在腔体变形时保持腔体的体积不变。 流体的重量使气球发生变形,这导致气球向外膨胀并陷入凹陷中;来自上方的压缩也会使它产生变形,这导致其向外和向上膨胀。由于这种压缩,气球内流体的深度会发生变化。我们想要求解这种深度变化,而不必求解流体流动的 Navier-Stokes 方程,因为我们只对静态(非时变)解感兴趣。 一个装满水的橡胶气球的中心被压缩。当气球被挤压时,最高点的位置和流体的深度会发生变化,从而改变静水压力分布。 合并静水压力 一个装有流体的容器会对容器壁施加静水压力: p(z)=p0+\rho g (z0-z) 其中,\rho 是流体的密度, g 是重力,z0 是容器顶部的位置,p0 是容器顶部流体的压力。由于气球中充满了不可压缩的流体,当我们用压头挤压它时,压力 p0,将会增加。 我们还可以从上面的图像中看到,随着气球被压缩,流体的深度也会发生变化。此外,似乎计算深度需要知道容器的顶部和底部的位置。那么,我们如何在深度上融入这种变化呢?接下来,让我们来看看怎么操作…… 如下图所示,气球内部施加的压力载荷有两个分量。压力载荷的第一部分是根据全局方程计算的。压力载荷的第二部分是由静水压力引起的。理想情况下,第二部分的压力载荷将基于流体的深度,但这个深度是一个我们不知道的变量。所以,我们输入一个只基于z位置的静水载荷,它可以有一个任意的零水平。 施加在气球内边界上的压力载荷是由全局方程计算出的压力载荷和静水压力之和。流体静压在求解过程中逐渐升高。 全局方程约束体积在变形过程中保持不变。 因此,这里看起来好像我们施加了一个压力载荷来约束体积和一个与 z 位置成正比的载荷,但是我们没有正确地计算静水压力,因为我们不知道 z0. 然而,事实证明,全局方程的作用可能比你最初预期的要多一些。 为了理解这一点,我们稍微重写了一下气球内部压力的方程: p(z)=(p0+\rho g z0)-\rho g z 我们马上就可以看到,这几乎与我们输入的压力载荷方程 p(z)= P0-\rho g z 完全匹配,除此之外可以看到,我们通过全局方程计算的压力是容器顶部的压力加上未知的顶部 z 位置的偏移量。所以,虽然我们只求解一个额外的变量 P0,但它解释了两种物理效应:由于体积约束引起的压力变化以及流体顶部 z 位置的变化。 由于这个模型包含几何和材料非线性以及由于接触引起的非线性,因此收敛到解可能很困难。为了解决这个问题,我们将使用负载递增来缓慢增加重力对模型的影响,并逐渐挤压气球。二维轴对称模型用来研究结构的对称性。 最大耦合算子被用于寻找腔内的最高点,以便进行后处理。 求解模型后,利用最大耦合算子对静压的大小进行后处理,计算沿气球内边界的最大z位置。 箭头表示随深度变化的静水压力载荷的解。 上图显示了气球内部的静水压力负荷。箭头的长度由以下表达式给出: WaterDensityg_const(maxop1(z)-z),其中 maxop1(z) 给出变形腔顶部的z位置。 结束语 在今天的示例中,我们对可变形容器(本例中是气球)中流体的不同深度进行了模拟。全局方程用于求解体积保持不变的流体压力,同时也考虑了气球变形时流体深度的变化。 通过使用这种方法,我们不需要显示地求解 Navier-Stokes 方程,就可以解决流固耦合问题,从而节省了大量的计算资源。如果您对这种类型的模型感兴趣,或想了解更多关于这种模型的细节,请与我们联系。

COMSOL 软件帮助优化 Mach-Zehnder 调制器设计
Mach-Zehnder 调制器是一种光通信调制器。使用 COMSOL 仿真软件可以了解其工作原理并优化设计。

在 COMSOL 中如何正确模拟流动
许多工程应用问题都涉及流体流动。除了代替风洞实验的经典 CFD 仿真外,电子设备冷却和通过流体输送反应物的化工行业,都必须考虑流动。
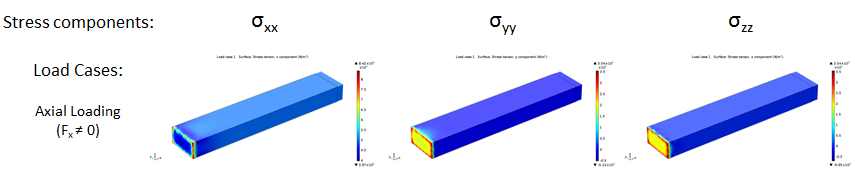
线弹性结构的刚度计算:第 2 部分
通过实现泊松效应,了解如何在 COMSOL Multiphysics® 中计算 2D 和 3D 线性弹性结构的刚度。关于计算刚度的 2 部分系列的第 2 部分。
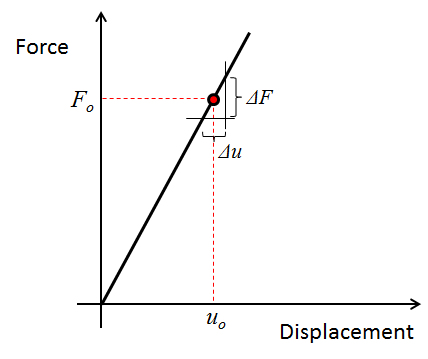
线弹性结构刚度的计算:第 1 部分
阅读本博客系列的第 1 部分,了解结构刚度以及如何在机械载荷下计算线弹性结构的刚度。

如何充分利用网络浮动许可证(FNL)?
从安装角度来看,COMSOL 单机许可证(CPU)和网络浮动许可证(FNL)的主要区别在于它们的安装和管理方式。FNL 不仅包含单机许可证的所有功能,还提供多个附加功能,能够大大改进您的工作流程,推动 COMSOL Multiphysics 随着贵公司的发展而不断扩展运用。
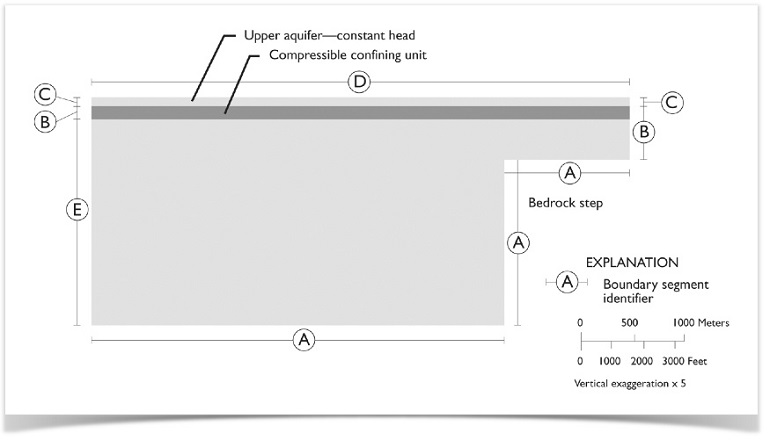
通过多孔弹性分析地基固结
您可以在构建结构之前进行多孔弹性分析,以帮助预测可能由多孔弹性变形引起的沉降。

使用 COMSOL 软件模拟地热过程
这是新的“地热能”系列博客文章的第一篇,我们将介绍模拟地热过程的基本概念以及大量相关的物理现象。我们还将向您展示一个地埋管换热器的示例模型。

借助 COMSOL API for use with Java® 实现建模任务的自动化操作
如今新产品的研发周期越来越短,为了在市场竞争中抢占先机,研发工程师和科学家们需要一件高效的工具,来帮助他们最快地获取计算结果,并摆脱重复性的例行工作。COMSOL Multiphysics® 正是他们需要的!COMSOL 软件拥有参数化扫描等多种内置功能,可帮助用户提高仿真工作效率。除了能够实现图形建模之外,它还拥有应用编程接口(Application Programming Interface,简称 API)。借助 API,用户便能对任意重复的建模步骤实现自动化操作。下面我们来了解一下 COMSOL API for use with Java®。
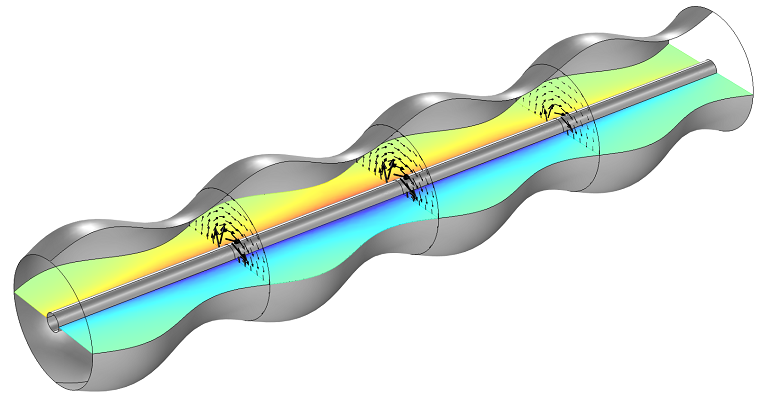
计算波纹波导的阻抗
您知道可以在 COMSOL Multiphysics® 中计算横截面不均匀的波导(如波纹波导)的有效阻抗吗?我们将在这里为您演示。

使用 COMSOL 计算单面磁体产生的力
磁体:它们是如何工作的?您可以使用 COMSOL Multiphysics® 和附加的 AC/DC 模块来计算单面磁体的力。
