
在“电磁设备”系列博客的第一部分中,我们介绍了如何模拟与弹簧和阻尼器相连接的线性电磁柱塞,并计算了柱塞的位置、速度及电磁力。在第二部分中,我们将为您展示安装有制动器/阻挡器的执行器,这个内部器件的作用正是约束线性运动。此外,我们还将讨论如何使用事件、磁场、移动网格 及全局常微分和微分代数方程 接口来模拟此类执行器中的接触与脱离行为。
模拟带制动器的线性电磁执行器
今天,我们将对第一篇博客中的 电磁柱塞教学模型进行一定的修改,也就是在装置内加入一个形状匹配的、可限制柱塞线性运动的制动器。柱塞的其他部件还包括:
- 多匝线圈
- 磁芯
- 非磁导向机构
- 磁性柱塞
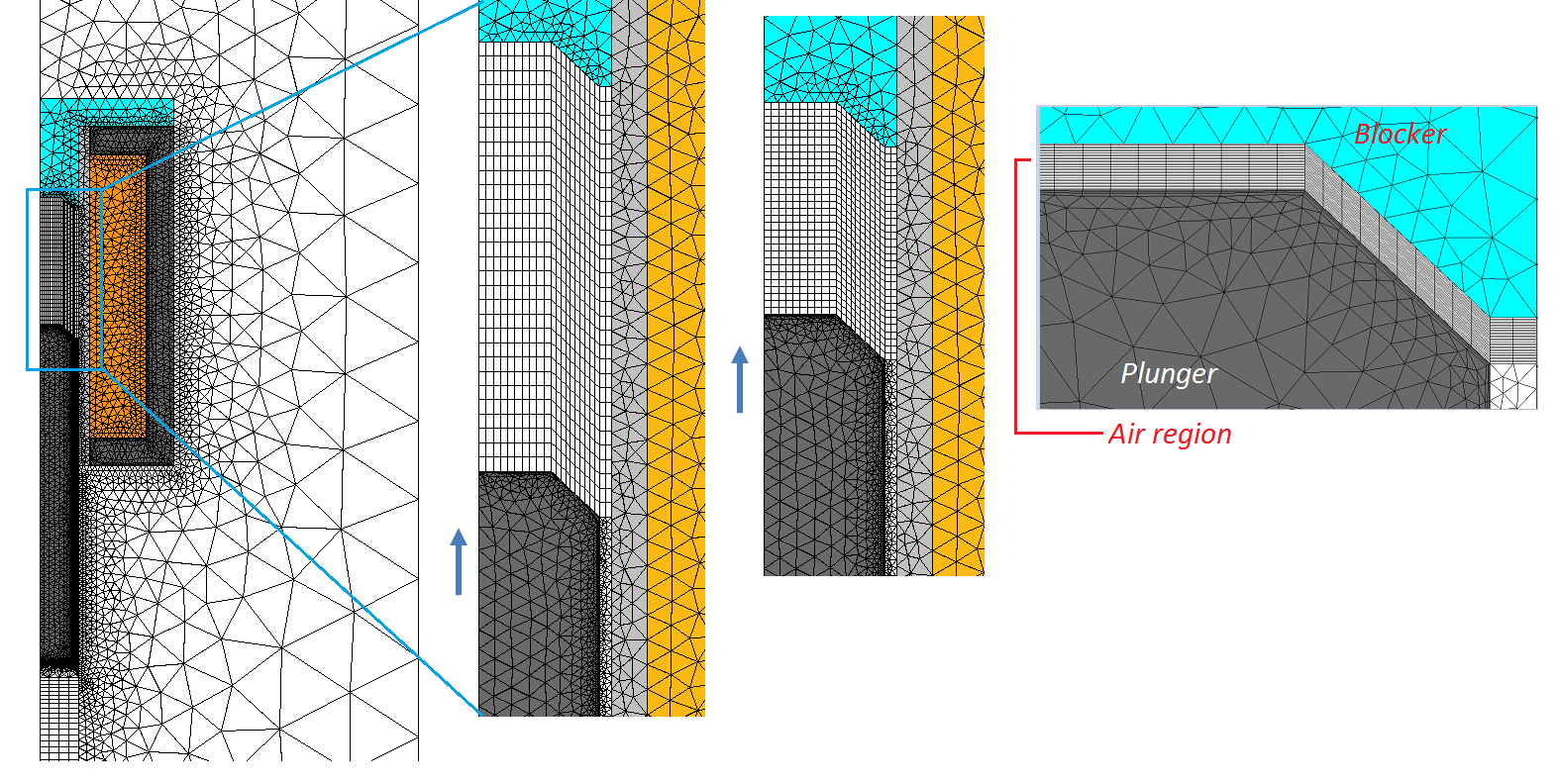
如下方的两张图像所示,我们将柱塞和制动器之间的空气域进行了分割,使其与线性振动的结构(映射网格)相匹配。在此结构中,阻尼器和弹簧连接到了柱塞的一端。
当瞬变电流通过螺线管线圈时,它会在柱塞和磁芯中产生一个磁场,磁场的存在使柱塞和磁芯之间产生了吸引力。这一现象随即使柱塞获得了加速度,背向弹簧朝上运动,直到与制动器发生接触。只要电磁力大于弹簧施加的回复力,柱塞就会与制动器保持连接状态。一旦与制动器接触,柱塞的速度便立刻变为零。然而当线圈关闭后,弹簧施加的力将占据主导,拉动柱塞返回到初始位置。我们将借助事件 接口来模拟装置中的接触与脱离机制。您可以点击这里下载模型文件及相关的演示幻灯片。
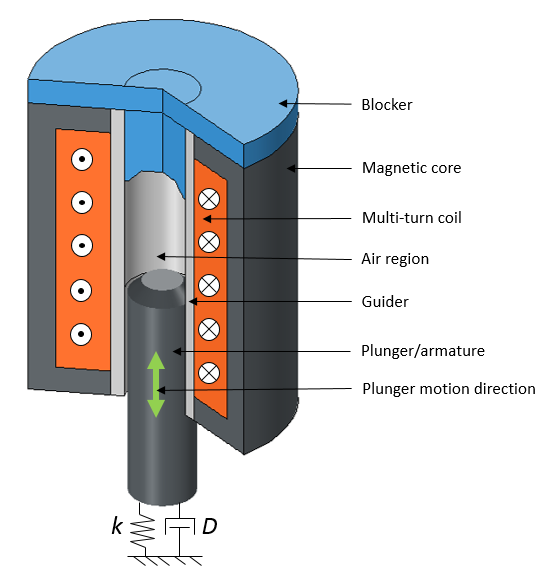
带制动器的电磁柱塞的三维视图(左图)及二维对称视图(右图)。
求解电磁场
在柱塞的仿真过程中,我们使用磁场 接口对设备的电磁场进行了模拟。为了模拟磁性元件(柱塞和磁芯),我们在该接口中添加了安培定律 节点,同时将节点中的“本构关系”设置为“H-B 曲线”。接着,我们添加了一个计算力 节点,这样就能够使用 Maxwell 应力张量方法来计算柱塞的电磁力。同时借助多匝线圈 特征,我们还使用了矩形函数来模拟螺线管绕组,并且传输瞬态电流。
模拟线性运动
为了便于模拟柱塞的线性运动,我们仅在移动域(即位于一致对左侧的柱塞和空气域)中添加了移动网格 接口。振动磁体及电磁柱塞的案例采用了相同的方式。不过,本文案例中的移动网格设置略为复杂,这是因为柱塞和制动器之间的网格体积几乎收缩为零。然而,体积为零的体网格是无法进行数值模拟。因此,我们给收缩网格的高度指定了一个有限值(本案例中为 0.5 mm),该值即表示柱塞和制动器之间存在接触。
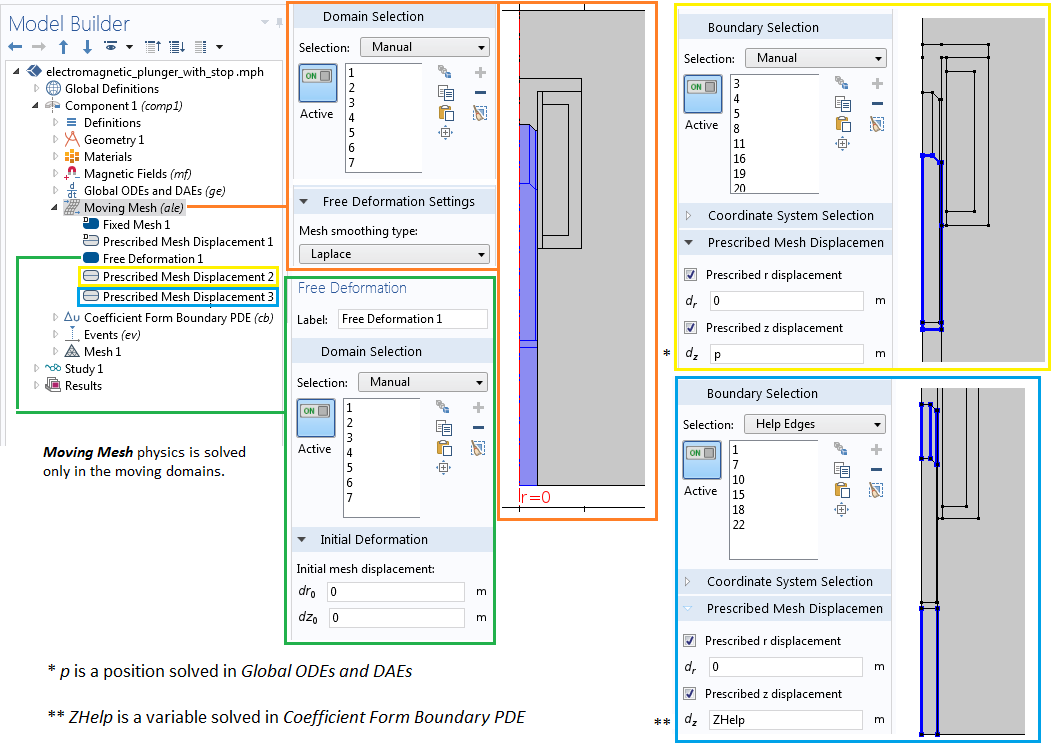
移动网格接口的设置,设置中描述的变量是从 系数型边界偏微分方程接口及 全局常微分和微分代数方程接口耦合而来的。
您可以在上图的设置中观察到,我们为柱塞和一小块空气域分配了位置变量 p,用于表示它们在 z 方向上的指定位移,而 r 方向上无任何位移。然而,针对收缩或膨胀空气域的侧边界(“帮助边”),其 z 方向上的指定位移被分配了一个新的变量 ZHelp。如下图所示,我们可以使用一个单独的系数型边界偏微分方程 接口来求解该变量。如需了解详细了解此功能,请参考关于如何使用移动网格接口模拟平移运动以及旋转和直线平移的博客文章。
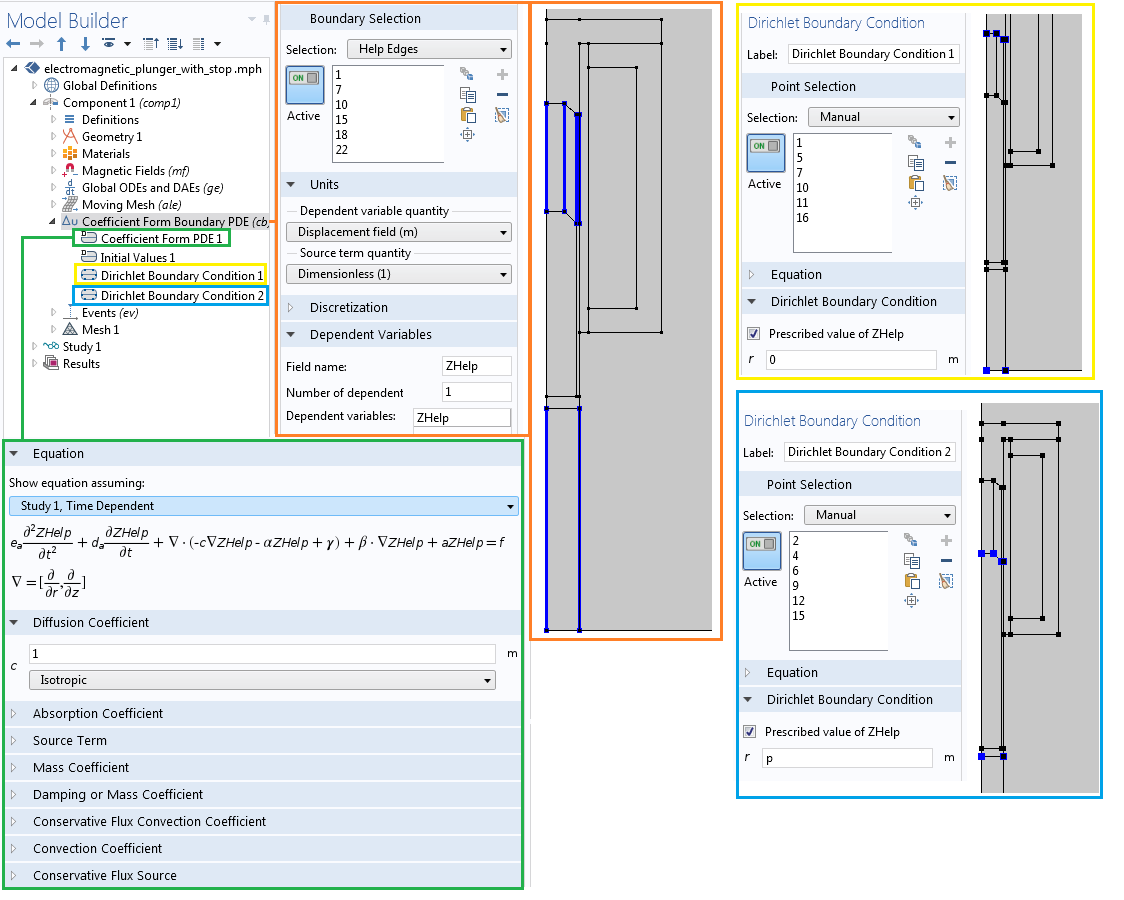
系数型边界偏微分方程接口的设置,它用于求解变量 ZHelp。
使用事件 接口模拟接触和脱离操作
接下来,我们将添加事件 接口,目的在于模拟柱塞与制动器/阻断器接触时,线圈电流被关闭后,以及柱塞下落时的情形。我们在数学 > 常微分和微分代数方程 接口分支中添加事件 接口,该接口的添加方式与 COMSOL Multiphysics 中的其他物理场接口类似。
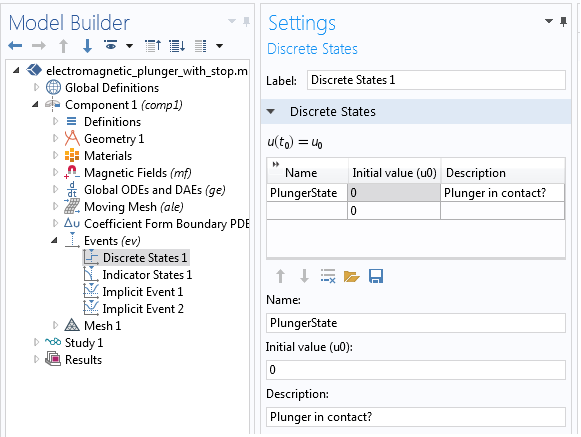
首先,在事件 接口中定义一对离散变量,它们满足两个条件:时间上不连续,并且十分适用于模拟柱塞的接触与非接触状态。如下图所示,离散变量 PlungerState 的初始值被设为零,也就是说,使用离散状态 特征时柱塞处于非接触状态。初始值为零表明了仿真开始时柱塞处于非接触状态。变量 PlungerState 被应用于全局常微分和微分代数方程 接口,这样能更准确地模拟处于接触和非接触状态的柱塞。该变量的离散值可为零或一,这取决于指示器状态。这一设置类似于我的同事 Water Frei 在之前发布的博客文章中探讨的有关恒温器的控制逻辑。
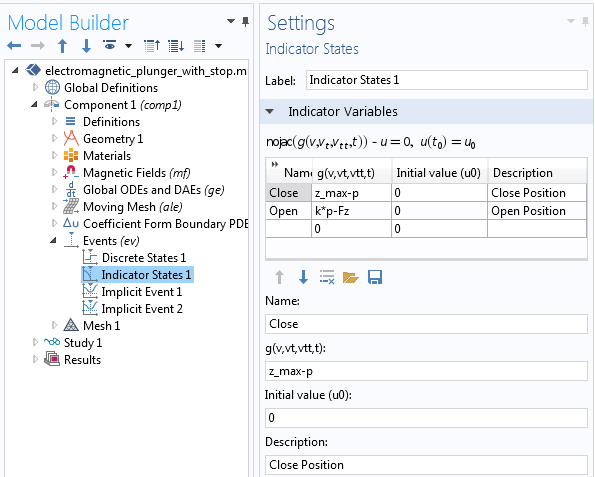
离散状态接口用于定义柱塞的状态,其中初始状态为脱离接触(左图)。事件接口中的两种指示器状态取决于柱塞的位置和受力(右图)。
接下来,我们要对指示器状态进行定义,即确定PlungerState 变量从 0 被触发为 1(或相反过程)的条件。指示器状态的意义是对指示事件将何时发生的变量进行定义。我们定义了两种指示器状态:关闭 和打开。关闭 指示器变量被定义为 z_max-p,它会平稳地由正值变化为负值。初始为正值说明了该变量的位置位于参数 z_max 之上,而本案例中 z_max 表示的是柱塞即将与制动器/阻断器发生接触的位置。按照相似的方式,打开 指示器变量被定义为 k*p-Fz,只要固定到柱塞的弹簧的力 k*p 大于柱塞的电磁力 F_z,该变量就会从负值平稳地变为正值。
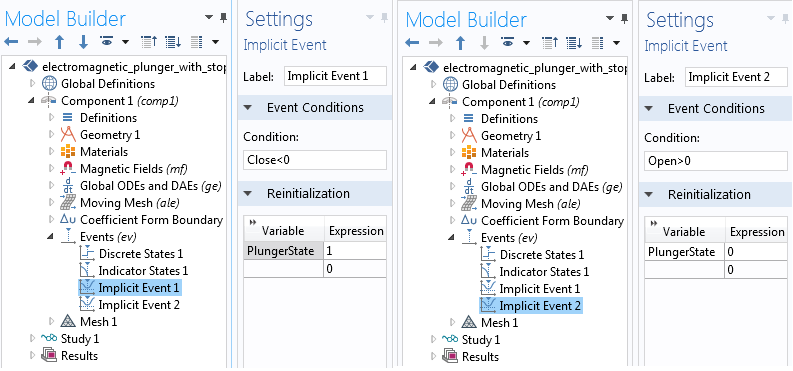
事件接口中的隐式事件设置,我们对其中的 PlungerState 变量进行了重新初始化。
由于不清楚这些事件触发的确切时间,因此接下来我们将在隐式事件 特征中编写恰当的逻辑条件来改变柱塞状态。指示器状态在打开 时大于零,在关闭 时小于零,如上图所示,我们据此添加了两个隐式事件 特征,将柱塞状态重新初始化为零或一。在瞬态仿真中,当满足逻辑条件时这些事件就会触发。事件被触发后,瞬态求解器便会停止运行,对全局常微分和微分代数方程 接口中位置和速度方程的 PlungerState 变量进行初始化,然后重新启动。我们将在下一节中对此进行讨论。
模拟柱塞装置的动力学特征
本系列博客文章的第一篇详细介绍了如何将全局方程引入全局常微分和微分代数方程 接口,并使用了多种不同的变量来描述与弹簧相连的电磁柱塞的运动,这些变量包括:
- 弹簧常数
- 阻尼系数
- 柱塞位置
- 速度
- 柱塞质量
- 柱塞受到的与弹簧弹力相反的电磁力
就柱塞状态 指示器而言,当 PlungerState 变量的值为一(即处于接触状态)时,方程(2)中的速度将被重置为 v=0,方程(3)中的位置将被重置为 p-z_{max}=0。但是如果柱塞处于非接触状态,那么方程(2)和(3)便可以分别表示速度方程和位置方程。

使用 全局常微分和微分代数方程接口和逻辑表达式来指定用于描述速度和位置的微分方程,柱塞接触和脱离接触的实现是借助 PlungerState 变量完成的。
分析结果
下图显示的是柱塞模型时域仿真的一组具有代表性的结果。仿真结果展示了是柱塞与制动器接触时,以及当线圈电流被关闭、柱塞下落时的情况。
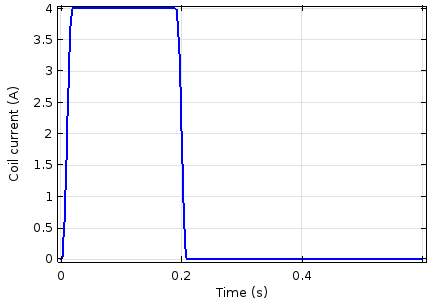
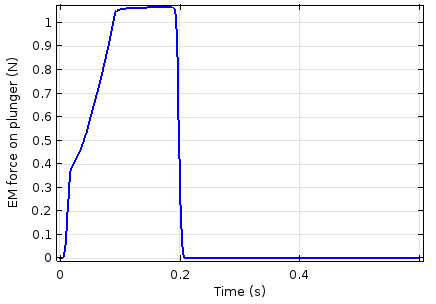
通过线圈的电流随时间的变化(左图)及电磁力随时间的变化(右图)。
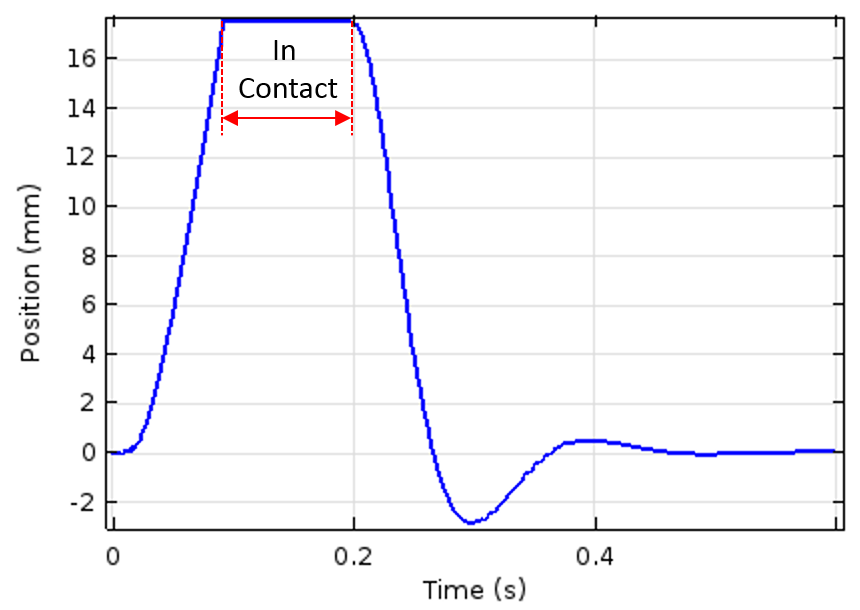
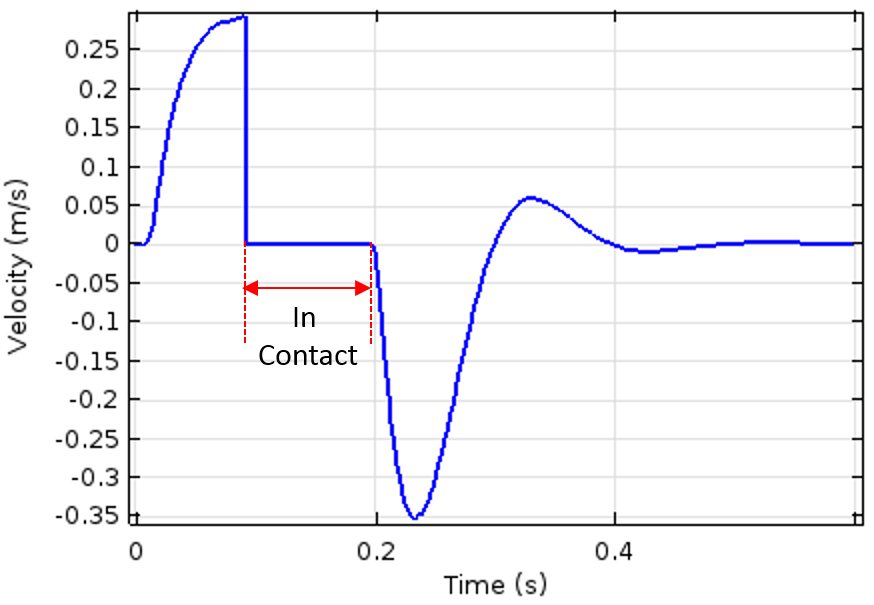
柱塞位置(左图)和速度(右图)随时间的变化情况。此外,绘图还显示了柱塞与制动器保持接触状态的时间间隔。
三维动画显示了带制动器的柱塞的磁通密度模的绘图(左侧);右侧图表与动画对应,实时显示了装置的位置、速度及通过线圈的电流。
总结
在本文中,我们通过引入事件 接口对柱塞的接触与脱离行为进行了模拟,从而扩展了第一篇博客文章中介绍的电磁柱塞建模技术。我们借助磁场 物理场计算出了柱塞的瞬态电磁力,并将柱塞的线性/平移运动耦合到移动网格 接口和系数型边界偏微分方程 接口,由此对柱塞的运动进行计算。此外,我们还将全局常微分和微分代数方程 接口与其他所有接口耦合起来,进而计算出柱塞的瞬态位置和速度。
了解更多关于电磁设备建模的信息
- 自己动手:在“案例下载”页面下载带制动器的电磁柱塞教学模型
- 返回上一步,探讨不带制动器的电磁柱塞教学模型
- 查看电磁设备系列的其他博客文章



评论 (12)
延飞 任
2018-06-11您好,我看到您的模型有一个制动器,它把衔铁的最大位移限制在了z_max,但是没有给它一个最小的位移。那么可不可以也给它加一个最小位移的限制呢,也就是说把衔铁的位移限制在一个范围内?期待你的回复:ryfsmile@163.com
Hello, I see that your model has a stopper, which limits the maximum displacement of the armature to z_max, but it does not give it a minimum displacement. Could we also add a minimum displacement limit to it, that is to say, the displacement of the armature is limited to a range?Look forward to your reply: ryfsmile@163.com
中彤 殷
2018-08-02为什么没有模型,能不能放上来或发我邮箱,谢谢!
Anonymous
2018-10-19殷中彤,您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
聪 郑
2020-07-22你好,请问有没有关于COMSOL中数学模块具体应用的案例呢,能不能通过全局方程对柱塞的最大位移和最小位移都进行限制呢?
wei bao
2020-07-24 COMSOL 员工您可以在以下页面“http://cn.comsol.com/models”中,以“方程”作为关键词搜索,可以找到很多PDE接口的应用案例
聪 郑
2020-08-13你好,在这个案例中对柱塞的运动进行了模拟,请问如何对柱塞到达最大位移后的反弹运动进行模拟呢?有没有相关案例?谢谢!
豆 土
2021-12-29您好,我刚开始学习,我是做电磁阀的,看了案例后,我有个问题,我的产品动铁芯和静铁芯之间的气隙只有0.5mm,吸合时,最终是要接触上的,我应该如果处理这个动网格了?
飞 李
2023-12-17模拟制动器线圈模型下载
hao huang
2023-12-18 COMSOL 员工该案例目前处于更新中,如有需要请发送电子邮件至 support@comsol.com ,获取模型文件。
先生 胡
2024-03-11你好 ,在文章最后呈现的三维动画绘图中,右侧的图表是随动画时间在不断绘制的,想咨询下这个方法是如何操作的,有无相关案例或教程 ,感谢!
Hao Li
2024-03-11 COMSOL 员工您好!
感谢您的评论。
在后处理>导出>动画中绘制一维绘图组的动图,调整动画帧与三维图一致。
目前还无法将三维图与一维图绘制在同一窗口中,本文的效果是通过后期组合的。
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
JACK wang
2025-11-19你好,我想用这个模型模拟磁通饱和的情况,随着电流I的升高,力F应该会稳定在某一个值不再明显增加,但是这个模型中并没有出现这种情况,请问我需要更改那些参数?我注意到固体中的安倍定则已经是B-H模型,我还添加了一个电流sweep,从0~20A,但是力一直随着电流成比例增大。期待你的回复:wjk19951114@163.com
Hello, I want to use this model to simulate magnetic flux saturation As the current I increases, the force F should stabilize at a certain value without significant further increase. However, this phenomenon is not occurring in this model. May I ask which parameters I need to adjust? I noticed that ampere’s law in solid already uses B-H cuvre, also I have added a current sweep from 0 to 20 A, but the force keeps increasing proportionally with the current. Look forward to your reply: wjk19951114@163.com