带标签的博客文章 传热模块

COMSOL Multiphysics® 在生物医学领域的 8 种应用
从机械心脏泵植入物、疫苗存储装置到血液分析仪,生物医学应用本质上通常是多物理场。因此,多物理场仿真可以帮助从根本上改变生物医学设备和流程的设计和分析方式。今天这篇博客,我们分享了 8 个真实的例子,来介绍生物医学领域的工程师和研究人员如何使用 COMSOL Multiphysics® 软件驱动他们创新的救生设计。 1. 左心室辅助装置 心脏衰竭,或称充血性心力衰竭,仅在美国就影响了超过 600 万成年人。当心脏不能向全身输送足够的血液和氧气时,就会发生这种常见的疾病。帮助缓解心力衰竭的一种方法是使用左心室辅助装置(LVAD),这是一种机械泵,植入胸腔后可提供循环支持。左心室辅助装置通常被称为 “移植的桥梁”,因为它们通常用于治疗等待心脏移植的病人。不仅如此,它们也可以被用作因客观医疗条件而无法接受心脏移植的病人的长期治疗方案。 正如预期的那样,左心室辅助装置的设计通常很复杂。他们需要: 足够的功率(大约10 瓦左右),可以正常运行 足够小,可以装进病人的胸膛 由与人体相容的材料制成 为了设计具备所有这些品质的左心室辅助装置,雅培实验室的研究人员使用了仿真技术。例如,他们使用 COMSOL Multiphysics 帮助设计了左心室辅助装置的离心泵。为了防止血液在泵内和泵周围凝结(设计 左心室辅助装置 时的一个常见挑战),研究人员在 左心室辅助装置 的设计中加入了一个磁悬浮转子。使用COMSOL,研究人员能够对 左心室辅助装置中的转子和湍流进行建模和分析。 磁悬浮转子的仿真(左上),泵腔内流体流动的 CFD 仿真(左下),以及 左心室辅助装置 的离心泵示意图(右)。 此外,研究人员还对左心室辅助装置的控制器进行了机械冲击分析,用于研究它的弹性。这个控制器有助于左心室辅助装置的供电、控制和性能监控。 “我每天都在使用 COMSOL Multiphysics,包括概念验证模型和模拟非常复杂的、具有详细 CAD 几何结构和多种相互作用的物理特性。我花费了数个月在一些复杂模型上以获得我所有需要的信息。” – Freddy Hansen, 雅培实验室高级研发工程师 2. 疫苗储存 根据美国疾病控制和预防中心的说法,疫苗储存在减轻常见可预防疾病的传播方面发挥着重要作用。然而,由于严格的温度要求,许多疫苗在存储过程中会变质,从而造成浪费。 作为全球公益项目的一部分,Intellectual Ventures 公司创新设计了一种被动式疫苗储存装置,用于将疫苗安全地运送到世界各地。它的设计只需要使用一批冰就可以将疫苗保持在 0°C~10°C。它的外壳具有多层绝缘,包括反射铝薄层、低导电空间和非导电真空空间。被动式疫苗储存装置不需要外部电源就可以工作。 在 COMSOL Multiphysics 中进行的被动式疫苗储存装置热仿真。 在设计阶段,研究人员在一个与撒哈拉以南非洲地区温度相似的环境室中测试了几个被动式疫苗储存装置原型的性能。为了优化被动式疫苗储存装置系统的设计,在建造原型之前,该团队使用了 COMSOL Multiphysics 以及它附加的各种产品,包括传热模块和分子流模块。 通过实验和模拟,该团队能够设计出一种容易运输的被动式疫苗储存装置,可以将疫苗冷藏长达一个月,从而能够将疫苗安全运输到世界各地,甚至是在电力有限或没有电的地方。 3. 消融技术 2020 年,肝癌是全球癌症相关死亡的第三大常见原因,导致了超过 80 万人丧生。这种疾病有时用消融技术进行治疗。这是一种微创治疗,可以在不切除肝脏肿瘤的情况下破坏它们。治疗肝癌的两种消融术包括: 射频消融 (RF),使用针状探针传递高频电流来加热和杀死肿瘤内的癌细胞 微波消融 (MW),使用针状探针发送电磁波来破坏肿瘤内的癌细胞 许多执行这类消融治疗的医疗专业人员面临的一个共同挑战是,他们无法获得有关这些程序有效性的实时反馈。为了解决这各问题,射频和微波消融技术的领先开发商——美敦力公司的一个研究团队使用仿真设计了具有更强的可预测性和有效性的新型消融探针。在他们的工作中,该团队使用 COMSOL Multiphysics 和附加的射频模块来优化探头的发射和接收特性。 4.老花眼 随着年龄的增长,我们的眼睛会出现越来越难以聚焦近距离的物体的情况。这种情况被称为老花眼,会影响到世界上大多数年龄到了65岁的人。老花眼的主要原因是晶状体形状的变化,晶状体是眼睛内部的一个微小结构。在我们年轻的时候,晶状体很薄且有弹性,但随着时间的推移,它会逐渐变厚,弹性变差。如果不加以矫正,老花眼会是造成视力障碍的最常见原因。 老花眼可以通过使用眼镜、隐形眼镜或简单的放大镜来缓解。一种更深入的治疗形式是屈光手术。但是,所有这些选择都有其自身的缺点和限制。 用于帮助研究老花眼的人眼模型。 为了推进老花眼的研究并治疗老花眼的根本原因,瑞士医疗器械公司 Kejako 的研究人员创建了一个人眼的 3D 机械模型。使用 […]

三维感应加热模型的高效网格划分策略
您对三维感应加热模型的高效网格划分策略感兴趣吗?在这篇博客中,我们将演示如何根据单元类型划分网格。
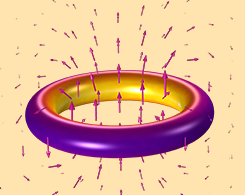
课程:在 COMSOL® 中模拟电磁线圈
获取有关使用 COMSOL Multiphysics 和 AC/DC 模块建模线圈的学习中心课程的概述,从设置线圈模型到分析电磁加热等等。

使用多层材料功能模拟薄层中的传热
COMSOL Multiphysics® 软件中内置了一组全面的功能,可用于计算薄层中的传热。关于如何使用这些功能以较小的计算成本获得精确的解,本文不做详细讨论。这篇博客,我们将重点关注与 多层材料 功能有关的问题:这项功能有什么作用?您的模拟如何从中受益? 编者注:这篇博客最初发布于2019年。现在已经更新以包括自 COMSOL Multiphysics 5.5 版本开始传热模块中增加的新功能。 模拟薄层中的传热 COMSOL Multiphysics 中提供了一些功能,可以考虑几何结构中薄层的特定传热属性,并且无需在几何结构中明确表征这些层,即可求解薄层中的热量传递。对于不同领域的应用,您都可以在层中定义电流和机械应力,例如电子元件和承受热应力的层压复合材料壳。 下图显示了不同温度梯度下钢柱中的温度分布。由于热导率低,安装在钢柱中部由两种不同材料构成的薄陶瓷部件起到隔热屏障的作用,并在陶瓷部分产生温度产变。陶瓷层在模型几何中被表示为一个面而不是两层薄体积域,以减少对网格大小的限制,这可能会使几何的不同部分具有高纵横比。高纵横比会使该部分的可视化变得非常困难。尽管几何结构中并未明确表征陶瓷部件,您仍然可以求解所有层的温度分布,并可以将其放大后更好地进行后处理,如下图所示。 使用 固体传热 接口和 薄层 节点计算的包含陶瓷层的钢柱中的温度分布。为了清晰地查看结果,将陶瓷层的厚度放大了 20 倍。 有关此模型的更多详细信息,请参阅 COMSOL 案例库中的复合保温层教程案例。 多层材料功能对传热仿真有什么好处? 多层材料 功能可以在两方面提高您的仿真经验: 在模型树的中心位置对多层壳属性的定义进行分组,以在不同物理场接口中访问。这样做是为了将介质定义从物理场定义中分离出来并减少建模工作,因为对于所有的物理场,介质属性只需设置一次。 通过允许如任意数量、任何位置和任意方向的层来增加灵活性。 接下来,我们来看看使用 多层材料 功能计算多层壳中的传热的功能设计的优势,考虑一个包含两层壳的几何结构: 在边界 1 上定义的第一层壳,由包含材料 1(顶部和底部)和材料 2(中间)的 3 层组成 在边界2上定义的第二层壳,由材料3构成的单层材料 包含多层壳的几何,以及施加在边界 1 和边界 2 上的材料。 多层壳作为表面被包含在几何结构中,但物理场方程可以通过增加自由度(DOF)在重建的体积域(下图中以红色显示)中求解。 施加在边界 1 和边界 2 上的多层壳的重建体积域(厚度放大了 10 倍)。 当模拟该几何结构中热量传递时,我们可以指定层数、每一层的厚度和材料。除了这些属性之外,还可以轻松访问高级参数,例如厚度方向的网格单元数量、边界上多层材料的取向和位置,以及层交界面的特定材料属性。 除材料外,多层壳的所有属性均由 多层材料 节点定义,包括多层壳的组成,每一层的几何和离散特性。物理节点(本示例中为 薄层)指向多层材料 节点(下图的中间部分);多层材料 节点指向用于定义材料属性的材料节点(下图的底部)。 包含多层壳定义在内的模型节点。 因此,您可以应用一个单物理场模型,模拟由不同数量和类型的层组成的多层壳的热传导。多层壳的特性在 多层材料 节点中定义。通过在模型树中将介质属性和物理模型的定义划分为两个不同部分,如下图所示: 模型树和 固体 节点的 设置窗口。 软件中提供的几个多层材料节点: 单层材料 多层材料链接 多层材料堆叠 多层材料 阅读博客使用复合材料模块分析风力发电机叶片,了解如何将这些节点组合起来对风力发电机复合叶片进行模拟。 上文,我们对多层材料 功能进行了介绍,接下来,我们需要回答两个问题: 如何利用此功能进行传热仿真? 该功能对仿真过程有什么帮助? 在 COMSOL Multiphysics® […]
仿真助力环境保护的 6 种行业应用
节能建筑和电器,安全的核废料储存,保存完好的淡水湖泊。 这些都是模拟如何保护环境的几个例子。

验证隔热屋顶 HAMSTAD 基准模型
HAM 是建筑材料和结构的一个重要研究领域,因为它会影响霉菌生长的速率和覆盖面积。
如何使用 PID 控制器插件模拟控制系统
PID 控制器可用于多种行业。这篇博客文章演示了如何在两个仿真示例中轻松合并 PID 控制器插件。
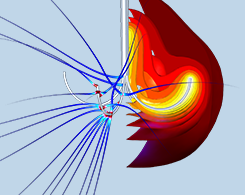
生物组织中的传热与热损伤分析
肿瘤热疗是利用热来治疗癌症的一种治疗方法,通过使用细微波天线或射频探头等设备,穿过患者的皮肤直接插入肿瘤中,来研究由热引起的生物学效应。
