带标签的博客文章 波动光学模块

利用对称性进行射频和波动光学模拟
2025年 4月 9日
我们可以通过利用电磁波模型可能具有的任何对称性来简化模型规模,并减少计算复杂度。点击此处,了解如何操作。

从光谱到颜色:借助仿真理解红玻璃是如何制造的
2024年 12月 9日
红色玻璃是怎样制成的?让我们使用波动光学仿真研究透射光谱来回答这个问题。

通过参数扫描追踪特征模态
2024年 8月 13日
在这篇博客中,我们将探讨在执行模态分析时,如何轻松地识别、排序和分组多个参数情况下的特征模态。

层状金属电介质双曲超材料仿真
2024年 6月 17日
学习如何模拟由周期性排列的银和二氧化硅薄层制成的超材料,并计算其介电常数张量分量。
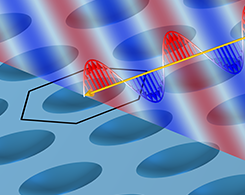
理解高阶衍射
2024年 1月 9日
探索如何使用埃瓦尔德球来研究平面周期性结构的衍射。(亲自动手实践案例模型,获得完整的图片!)
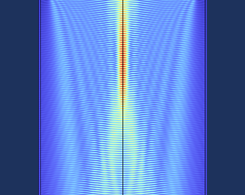
使用 COMSOL Multiphysics® 开发用于设计超透镜的仿真 App
2023年 9月 21日
这篇博客,我们将探讨如何构建一个用于反射超透镜设计的仿真App,它可以很容易地编译成一个独立的应用程序。
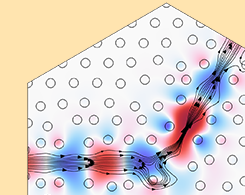
电磁学中的形状优化:第 1 部分
2022年 11月 22日
了解如何利用形状优化来改进波动光学应用的设计。第 1 部分。

在 COMSOL® 中对表面等离激元进行建模
2022年 10月 12日
由于它们在纳米级操纵光方面的潜在应用,表面等离激元(SPPs)具有很大的研究兴趣。在这里了解如何对它们进行建模。
