验证边界元法在静磁学建模中的应用

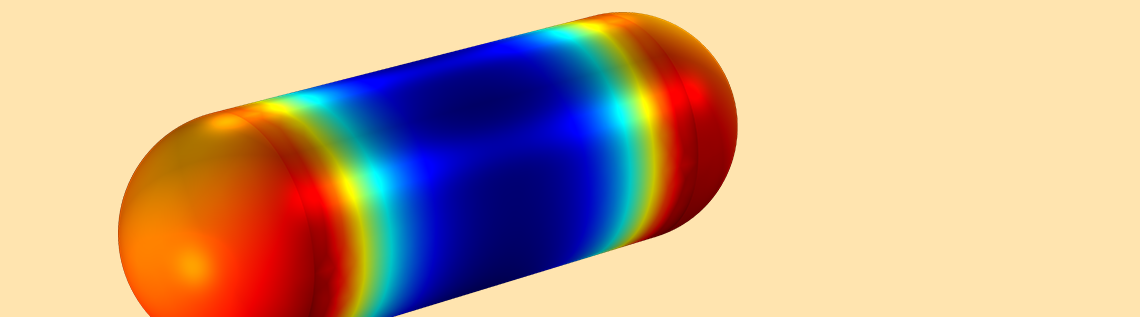
边界元法（BEM）可以替代静磁学建模中的有限元法吗？在由三部分组成的系列教程中，我们使用麦克斯韦应力张量执行电磁力计算，以演示边界元法的效能。我们根据解析模型验证结果，并将结果与有限元法的结果进行比较，以显示边界元法在这方面的价值和实用性。请继续阅读下文，了解您将在系列教程中学到的内容。

边界元法和有限元法的比较

边界元法是一种数值仿真工具，可用于代替（或结合）有限元法来分析静电学、静磁学、声学、腐蚀等。与有限元法不同，边界元法仅需要表面网格，因此无需在整个计算域中生成体网格。

边界元法在适当的环境下应用时，计算效率高，且易于实施。该方法将各个自由度相连接，适用于无限域、各向同性材料和导线。不过，边界元法不适用于具有非线性或一般非均匀材料的模型。

以静电学为例，在这个领域，使用边界元法可以简化各种建模任务，包括：

• 模拟电线和各向同性材料
• 设置无限域
• 任意距离的后处理

在某些情况下，您可以使用边界元法对某些区域进行建模，使用有限元法对另外一些域进行建模，然后将这两种方法结合起来体验每种方法的优势。

电磁力验证系列教程中的两个平行磁棒的模型。

现在您已经了解了边界元法的基本概要，接下来可能想知道您可以用它做什么。首先，当精确的通量计算十分重要时，该方法非常有利。在本系列教程中，我们研究了将边界元法作为静磁学建模环境下有限元法的替代方法——特别是使用麦克斯韦应力张量计算电磁力。

我们看一下边界元法与有限元法的比较情况，然后根据解析模型验证边界元法。

执行和验证电磁力计算

本系列教程采用以下产品：COMSOL Multiphysics® 平台和附加产品“AC/DC模块”。教程中用于验证电磁分析的一些技术包括：

• 使用圆角，高级网格划分和外力探针表面来提高精度
• 比较多种网格尺寸下的边界元法和有限元法
• 通过参数化扫描研究网格收敛

本系列的第 1 部分向您介绍了将在第 2 部分和第 3 部分中使用的模型几何结构，并详细说明了如何逐步构建这些几何结构。

注意：经验比较丰富的软件用户可以跳过第 1 部分的介绍，直接阅读第 2 部分。如果您是 COMSOL Multiphysics 初学者，这些说明将帮助您了解建立模型几何结构的基础知识。

第 2 部分中的模型几何结构由半球体中的单个棒组成，第二个棒用于说明对称性。为了执行第 3 部分中的转矩分析，我们将单个棒放置在球形域中，并用三次曲面将其封装，该曲面向棒施加外场。

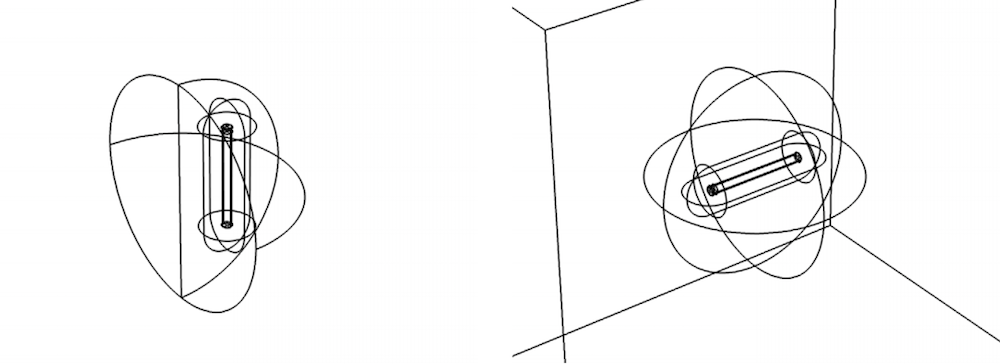
电磁力（左）和电磁转矩（右）模型的几何结构。

用边界元-有限元混合法计算磁力

有许多不同的方法来确定刚体上的电磁力。使用麦克斯韦表面应力张量计算力时，对磁场（H）和磁通密度（B）进行精确的磁通积分是非常重要的。

边界元法在这方面相当强大，在计算力时具有潜在的优势。与有限元法不同，当使用边界元法时，垂直于边界的通量直接作为自由度输入，这样可以进行精确的通量计算，而无需反作用力积分或弱约束。通过使用边界元法求解这里讨论的模型，并将结果与有限元法和解析模型的结果进行比较，我们可以验证边界元法在电磁力计算中的应用。

谈到静磁学，有两种理论架构较为普遍：

1. 磁极
2. 原子电流

这里使用的解析模型包含静磁电荷，在数学上等同于静电学，因此我们以磁极为基础建立此模型。

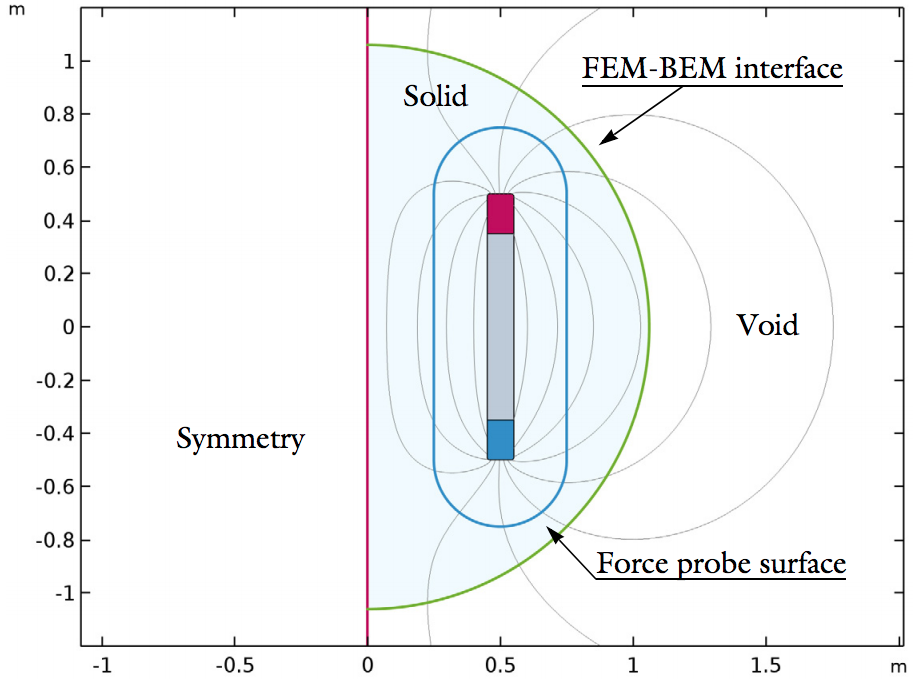
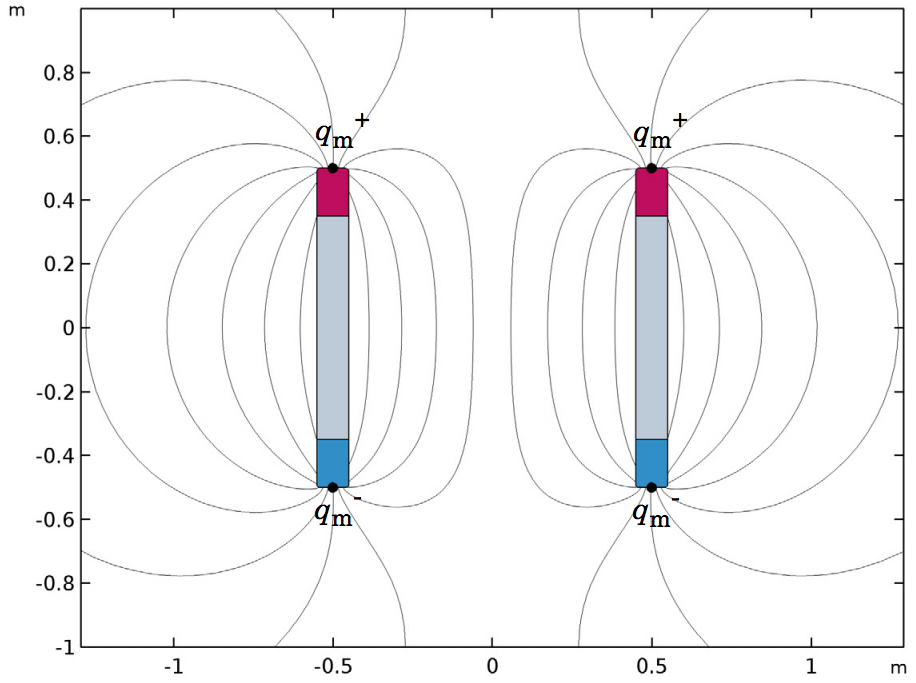
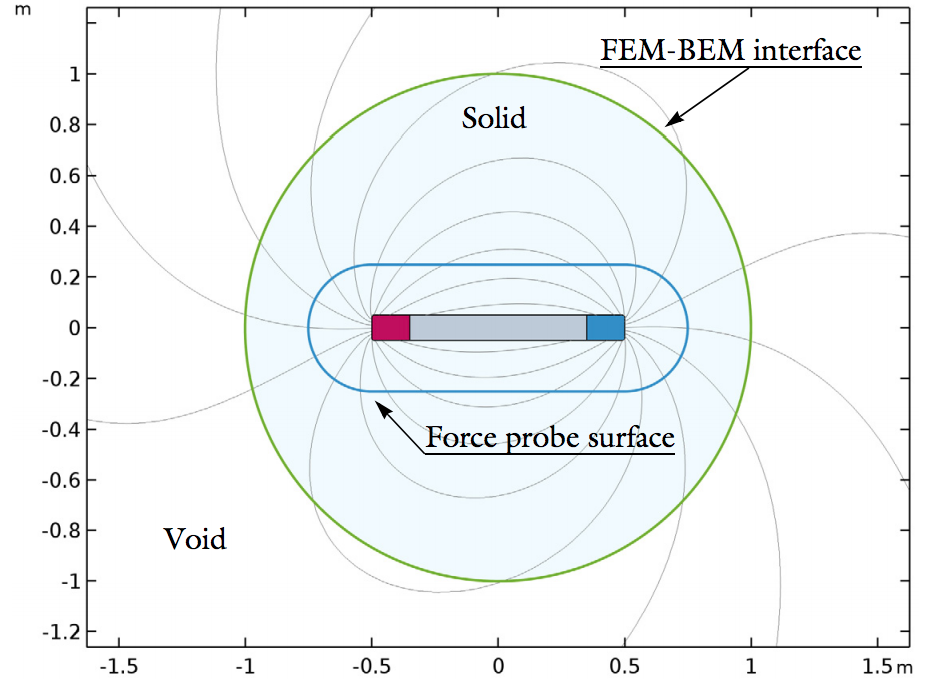
电磁力验证模型的二维几何结构（左）和用作验证根据的解析模型（右）。

验证模型包含两个长 1 米、间隔 1 米的磁化棒。棒内的剩余磁通密度经过专门选择，使得解析模型预测的棒之间的排斥力正好为 1 牛顿米。我们可以使用这些条件来比较数值结果并确定它们的精确度，因此这些条件非常重要。

比较 2 种电磁力计算方法

通过观察结果，我们发现边界元法可以产生平滑的场，即使对于具有相对粗化网格的模型也是如此。

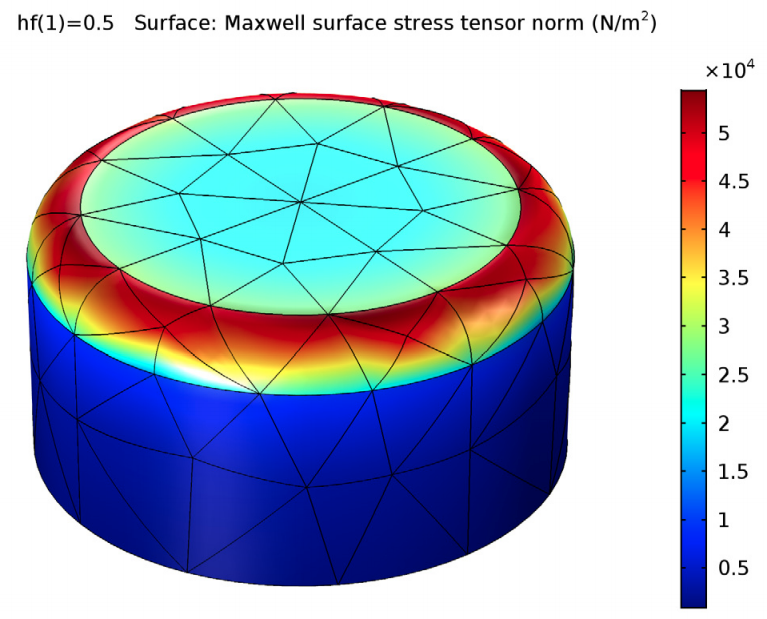
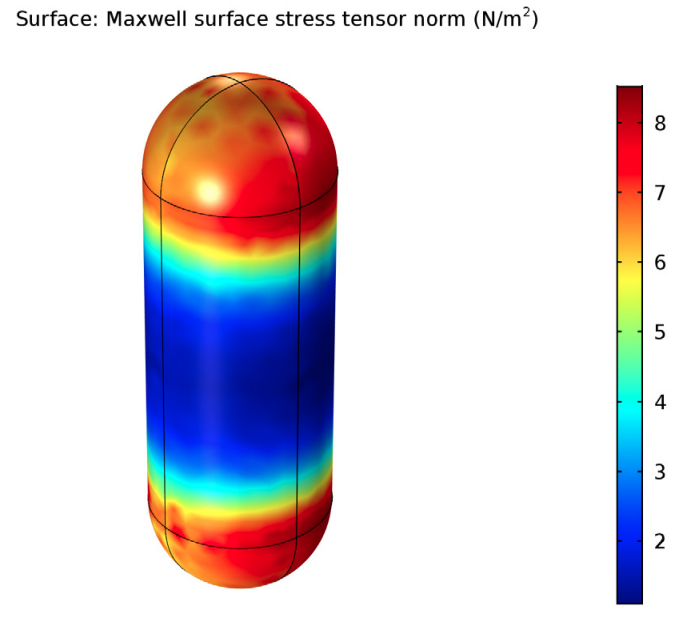
麦克斯韦表面应力张量，用于计算棒表面（左）和探针表面（右）的电磁力。

将不同网格尺寸的边界元法和有限元法结果与解析模型结果进行比较时（见下图），我们发现，边界元法可以为粗化网格生成准确的结果；与此不同，有限元法需要在棒上使用较细化的网格才能达到相同的精度。

另外，请注意，力探针模型的结果更准确。应力张量计算的磁体一定距离处的结果更准确，这就是力探针模型与解析模型结果较为一致的原因。

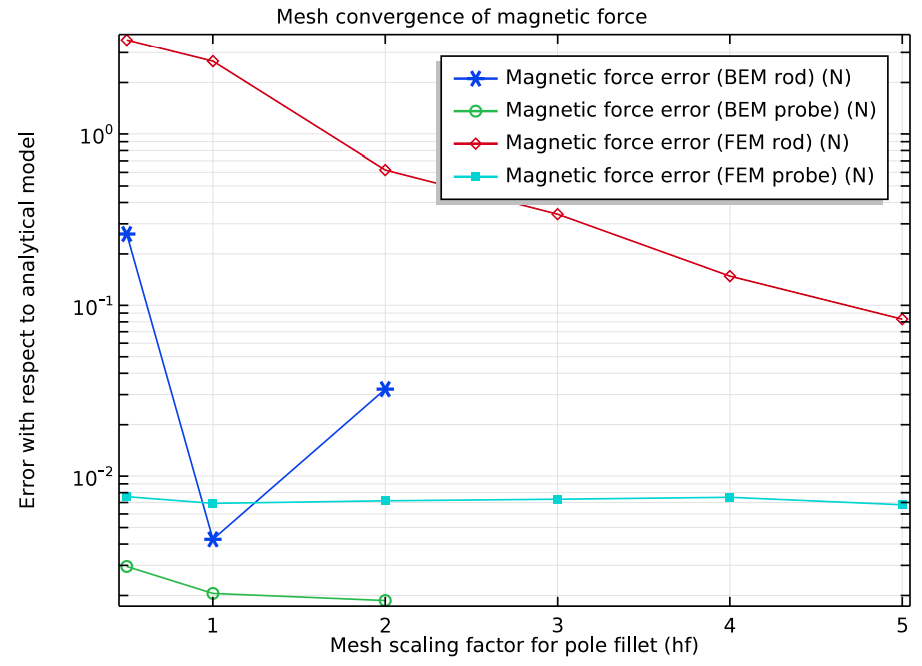
棒表面使用边界元法（深蓝色）、探针表面使用有限元法（绿色）、棒表面使用边界元-有限元混合法（红色）和探针表面使用边界元-有限元混合法（浅蓝色）进行力计算的相对误差范围。

仿真结果还表明，应力集中在磁体的圆角上，这解释了为什么在具有锐边的刚体上计算力通常不准确。实际上，为具有锐角的磁体计算力可能导致高达 2000％ 的误差。边界元法可以为您的结果生成平滑场，即使对于具有相对粗化网格的模型也是如此。

用边界元法分析磁矩

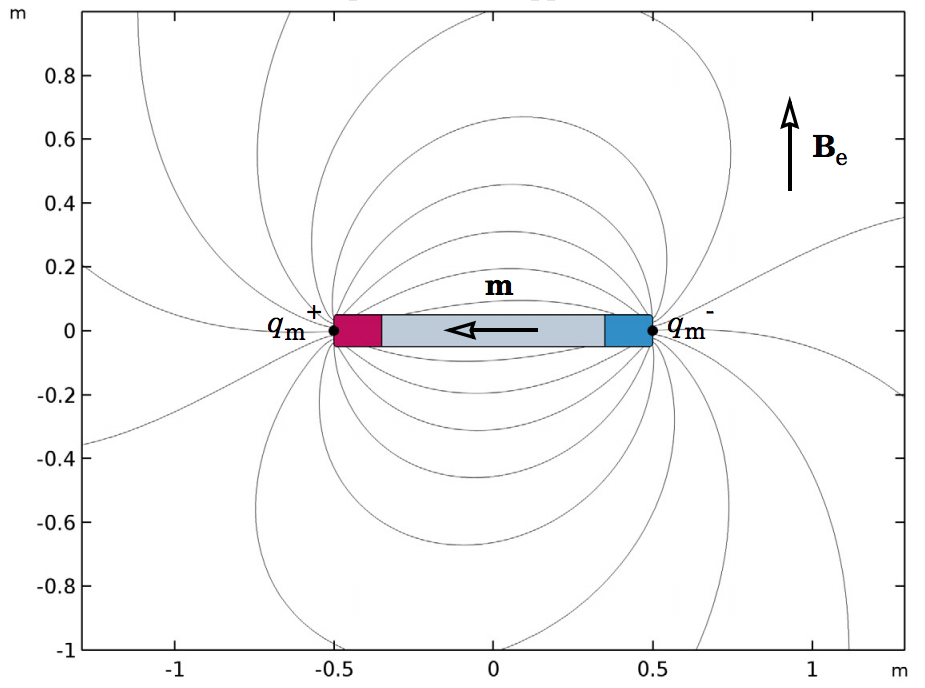
第 3 部分继续分析不同几何结构的磁力边界元-有限元混合法验证模型。将一米长的单个磁化棒放置在垂直的外场 B_e 中（下方，右侧）。选择外场的强度，使得解析模型精确地预测棒上的转矩为一牛顿米。这样，我们可以使用解析模型来验证棒上转矩的数值结果。

用于转矩分析的模型几何示意图（左）和解析模型示意图（右）。

对于边界元法，结果类似于电磁力教程的结果。有一些包含粗化网格的平滑场，应力集中在圆角处，与解析模型相比，精度相当高。

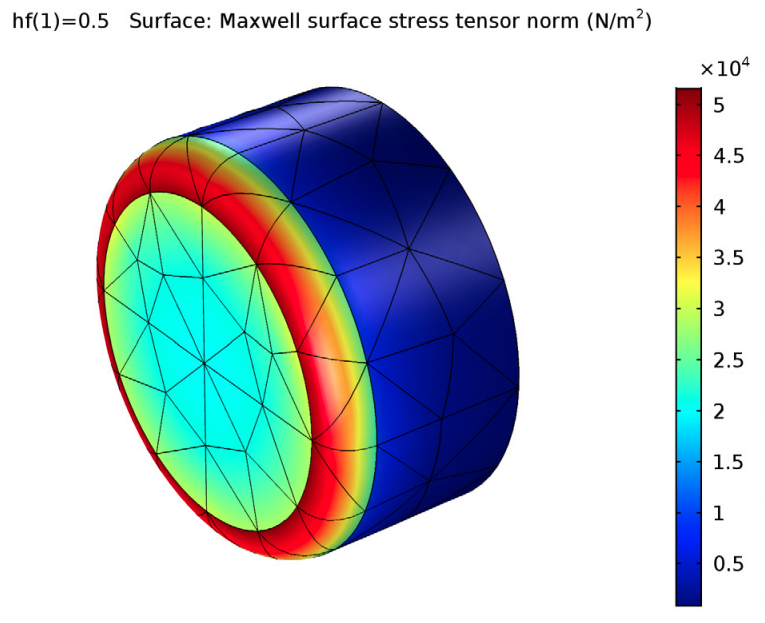
麦克斯韦表面应力张量，用于计算棒表面（左）和探针表面（右）的电磁转矩。

边界元-有限元混合法的结果误差范围较大，与第 2 部分非常相似。对于边界元法和混合法，探针表面的结果也比棒表面的结果更精确。

正如这两个模型所证明的那样，边界元法在适当条件下正确使用时，对于静磁建模是有利的。

后续操作

跟随电磁力验证系列教程，全面了解如何执行和验证电磁力计算。您可以单击下面的按钮进入“案例下载”页面，从中访问 PDF 版本的说明并下载 MPH 文件。（请注意，您需要具有 COMSOL Access 帐户和有效的软件许可证才能访问模型文件。）

扩展阅读

在以下相关博客文章中找到更多有关电磁学建模的信息：

• COMSOL Multiphysics® 电缆建模：6 节系列教程
• 如何创建包含导线、表面和实体的静电学模型
• 是否应该在电磁热分析中对几何结构进行倒圆角处理？