
等离子体建模通常需要了解电子能量分布函数(EEDF)以及电子迁移率和扩散率等传递属性。为了用玻尔兹曼方程精确计算这些量,我们还必须知道电子密度(可能还要知道所有受电子碰撞反应影响的物质的密度)。然而,电子(和物种密度)是等离子体模型的输出,这是一个自相矛盾的问题。我们通过一个示例 App 看看如何克服这个难题。
EEDF 和等离子体建模
虽然精确地对等离子体建模很重要(比如为了匹配实验结果),但我们也希望模型尽可能简单。为了保持模型简单,我们通常选择麦克斯韦或德拉文斯坦EEDF 和恒定的电子迁移率。然后可以使用爱因斯坦关系自动计算传递属性。然而,在低压放电时,EEDF 经常明显偏离麦克斯韦 EEDF。在较高压力下,高加速场也可能导致非麦克斯韦分布。
为了获得更精确的 EEDF 曲线,我们可以求解玻尔兹曼方程(通常是两项近似)。COMSOL Multiphysics® 软件甚至为此提供了一个专用接口,命名为玻尔兹曼方程,两项近似 接口。
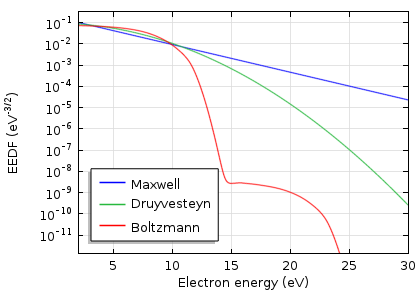
平均电子能量为 5eV 时典型氩气放电情况下,麦克斯韦、德拉文斯坦和玻尔兹曼分布函数的比较。
然后我们遇到了这个自相矛盾的问题。要用玻尔兹曼方程计算 EEDF,我们必须知道电子密度。但这是等离子体模型的结果,我们需要先使用 EEDF 和传递属性来求解。
我们怎样才能摆脱这种循环?一种方法是使用迭代过程。第一步是猜测平均电子密度,用它在玻尔兹曼方程,两项近似 接口中计算 EEDF 。接下来,我们用 EEDF 计算等离子体模型,得到一个新的平均电子密度。然后我们必须再一次次重新计算 EEDF、等离子体模型等。
手动逐步执行此过程可能很麻烦,比较好的方法是使用“App 开发器”设计一个自动执行此过程的 App。我们看一下“案例下载”中的一个例子。
用 App 模拟非麦克斯韦 EEDF 等离子体
要使用这个 App,我们只需要对电子密度和激发氩原子的摩尔分数进行初始猜测,可以调整外加电压、反应器长度、气体温度和其他变量的值,也可以在右侧的电极上添加一个快速电路。接下来,我们选择我们想要的 EEDF 类型(玻尔兹曼、麦克斯韦、德拉文斯坦或广义型)。
当我们单击全部计算 按钮时,App 会自动在计算等离子体模型和 EEDF 模型之间切换。每次计算的等离子体模型的平均电子密度被用作输入参数来确定新的 EEDF,这种情况一直持续到计算等离子体模型前后两次的平均电子密度的偏差低于某用户定义的值。或者,我们可以分别单击仅计算玻尔兹曼 按钮或仅计算等离子体 按钮来仅求解玻尔兹曼模型或等离子体模型。
至于我们的结果,我们得到了等离子体物质密度,如电子和离子密度,以及电子温度。还看到了不同平均电子能量的 EEDF 和电子传递属性。使用玻尔兹曼分析 下的指定位置的 EEDF 选项卡,我们可以检查反应器几何结构中每个点的 EEDF,并将计算出的 EEDF 与麦克斯韦 EEDF 进行比较。此外,该 App 还计算物质密度和平均电子能量的平均值。
底层等离子体和 EEDF 模型
我们看一下底层模型。要使用非麦克斯韦 EEDF 模型对等离子体进行建模,我们需要两种模型:
- 等离子体模型
- 计算 EEDF 的模型
App 中使用的等离子体模型是一个简单的一维辉光放电模型,类似于案例下载中的一个模型。等离子体反应器的左电极接地,同时向右电极施加电压。我们在 App 中设置此电压的值(以及反应器长度、气体压力和温度等其他参数)。

等离子体接口的模型树。
我们还使用一个简单的一维模型来计算 EEDF。这里,x 轴不代表空间坐标,而是电子能量。然后,我们对平均电子能量进行参数化扫描。例如,该模型对应于氩气玻尔兹曼分析教程。

玻尔兹曼方程,两项近似接口的模型树。
需要注意的是,这个 App 使用反应器中的平均电子密度来计算 EEDF。因此,EEDF 仅取决于放电的平均特性。实际上,EEDF 应该在反应器几何结构中的每个点进行计算,计算量非常大,因此本例中我们不做计算。
了解更多关于使用 COMSOL Multiphysics® 进行等离子体建模的信息
- 浏览以下与等离子体建模相关的博客文章:






评论 (0)