如何在热膨胀仿真中提供结构稳定性

假设你想计算物体的热膨胀和应力，提供边界上的热通量和温度约束，然后计算，可是并不收敛。通常，这种结果归因于缺乏位移约束。问题是，提供不引起人为应力的约束并非易事。今天，我们介绍 COMSOL Multiphysics® 软件中的刚体运动抑制 特征，你可以使用该特征自动找出所需的约束。

结构分析中的运动学约束

在静态或准静态结构分析中，我们要寻找的是均衡解。物体可以自由变形，但不能像刚体一样自由移动或旋转。为此，反作用力必须与作用力相互平衡。反作用力来自对位移和旋转的约束。在二维中，我们需要防止发生两个位移和一个旋转；在三维中，我们需要约束三个位移和三个旋转。

如果不提供约束，则不平衡的力会移动或旋转对象，这与平衡假设不一致。因此，问题有多个解，它们因刚体运动而互不相同。得到的刚度矩阵是奇异的，稳态求解器无法收敛。

看待这个问题的另一种方式是从数学角度。平衡方程是椭圆偏微分方程，需要足够的狄利克雷边界条件才能得到唯一解。

由于惯性项的存在，这在动态分析中不是问题。与静态分析中不应该存在不平衡力不同，动态分析中的不平衡力可以自由地产生加速度。其对应的方程是双曲线型的，不需要狄利克雷边界条件就可以满足计算要求。请注意，我们所讨论的是动态分析，而不是仅忽略了惯性贡献的准静态瞬态分析，我们忽略了惯性贡献。我们在本文中讨论的例子是静态分析。

无法收敛：热膨胀问题

假设我们想研究由热膨胀系数（CTE）不同的基板和涂层制成的层合板中的应力。当层合板无应力时，涂层在 800℃ 的温度下沉积在基板上。如果我们将温度降低到 150℃，希望找到由 CTE 不匹配引起的应力。在这个例子中，由于我们知道各处的最终温度，因此不需要求解传热问题，可以直接将热膨胀 属性添加到线弹性材料 节点。

没有足够位移约束的热膨胀仿真无法收敛。

具有较高 CTE 的基板在冷却时比涂层更容易收缩。但是将它们粘合在一起会迫使它们在公共边界处有相同的位移。因此，预计会出现基板中的拉伸应力、涂层中的压缩以及结构的整体弯曲。然而，此时单击计算 只会给我们带来“找不到解”类型的收敛错误，这是因为，分析没有唯一解。

用“强力”实现收敛

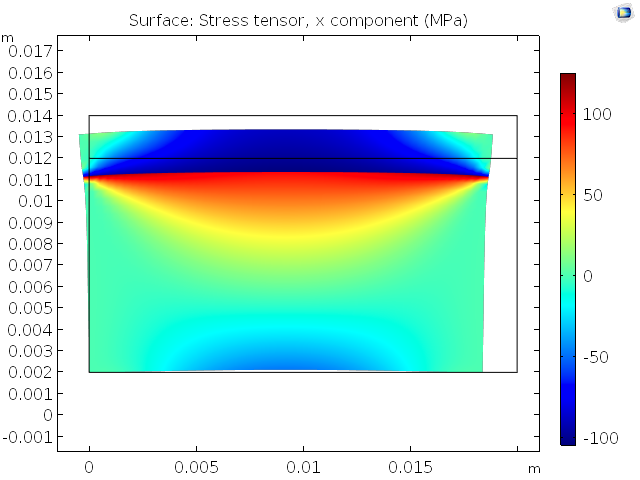
如果我们在某些面（比如左边两个面）上添加固定约束，肯定能防止刚体位移或旋转。或者，如果我们在左侧面和底部面添加对称条件，约束非平行面上的法向位移，也可以防止刚体运动。无论是哪种情况，模型都会收敛。以下是在将位移放大之后的变形构型上绘制的 x 方向上的法向应力结果。

左图为具有固定约束情况下的解，右图为具有对称条件情况下的解。

上述解具有非常不同的应力分布和变形模式。两个解至少有一个应该是错误的。比如说，如果我们的问题是对称的，当只使用四分之一仿真域和对称边界条件。另一个好处是，利用对称性可以减少计算内存和时间需求。如果底部有相同厚度的第二层涂层，我们就能做到这一点。如果我们人为地强制对称，我们将得到一个收敛的、但不合理的解。

如果这个层合板随意放在桌面上，并且没有对称性，则上述两个边界条件都会得出错误的解。收敛不充分：我们想要收敛到一个物理上正确的解。为此，我们希望提供约束来稳定模型而不扭曲应力状态。

得到精确解的手动方法

如果问题具有足够的对称性，最好使用这些对称性，如上所述。否则，我们需要给出不引起人为应力的位移约束。这里有几种选择。一种选择是使用“3-2-1”方法：

1. 选择三个完全分离的非共线点（对于三维模型）
2. 在三个方向上固定第一个点
3. 将第二个点限制在从点 1 到点 2 的矢量法线的两个方向上
4. 将最后一个点限制在垂直于由三个点形成的平面的方向上

注意：对于二维模型，该方法简化为固定第一个点，并将最后一个点限制在垂直于两个点形成的直线方向上。

使用点约束稳定二维结构。

手动指定不影响应力状态的位移约束后的结果。

尽管可以采用这种方法，但在较复杂的问题上这种方法可能会变得棘手。设想一种结构，其中边界与坐标方向没有整齐对齐，如上述对象中所示。现在，我们必须约束位移 u 和 v 的一些函数，而不仅仅是第二点处的 v。这在三维问题中很容易失控。此外，当使用其他结构力学接口（如梁 接口）时，自由度并不总是位移。我们来看一个简单而唯一的解。

自动刚体运动抑制

无论空间维度或结构理论（接口）如何，我们都可以使用刚体运动抑制 节点，这样 COMSOL® 软件能够处理缺失的位移约束。此特征自 COMSOL Multiphysics 5.3 版开始提供。选择“模型开发器”中的固体力学 > 域约束 > 刚体运动抑制，可以访问此节点并向其添加域。

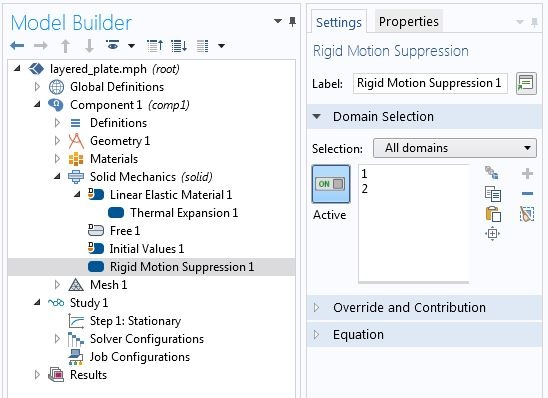
二维问题的刚体运动抑制。

我们通过自动逼近刚体运动抑制的方法得到以下结果：

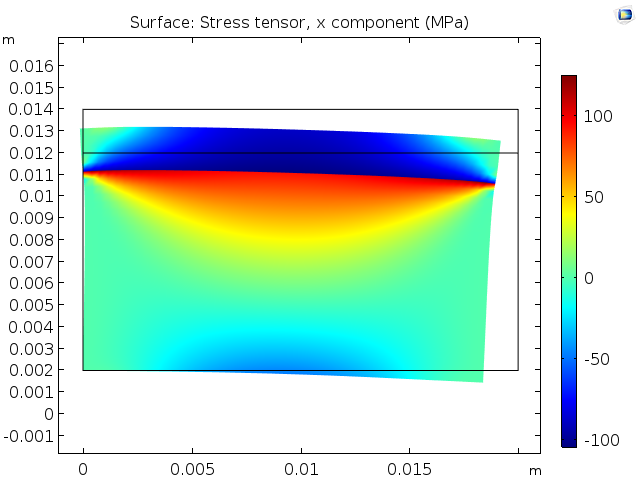
温度变化和 CTE 不匹配引起的应力。

在上述解中，应力是相同的，但变形后的形状看起来不同。事实上，他们的不同之处在于刚体运动。当我们手动提供刚体运动抑制时，我们从无数个解中选出一个。自动刚体运动抑制可能选择了另一个。因此，刚体运动的位移可能不同，但应变和应力是相同的。

在当前示例中，我们可以将任一域或两个域都添加到刚体运动抑制 节点。由于两个域是粘合的，防止刚体在一个域中运动就足够了。在这种情况下，域的选择不会改变所获得的应力状态。它只是改变了软件决定约束的点。

现在我们来看一个三维问题。考虑多种类型的结构力学接口，并使用传热 接口来获得不均匀的温度分布。这是一个模拟加热电路装置的电热产生、传热以及机械应力和变形的示例。

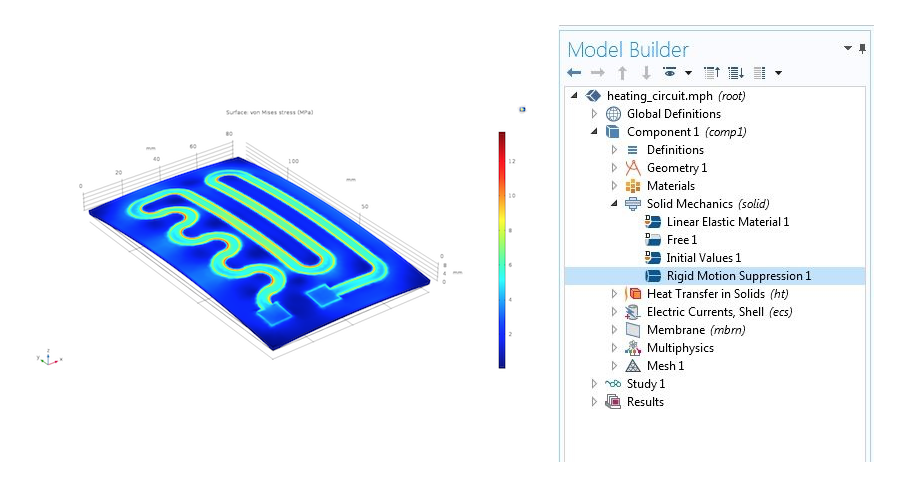
由加热电路中的 CTE 不匹配引起的 Von Mises 应力。

结构力学模块用户指南 中描述了 COMSOL Multiphysics 软件用于识别与刚体运动抑制 特征一起使用的点和约束的算法。

防止误用的警告

通常在热膨胀仿真中，温度变化是应力的唯一激活的源。但如果存在机械力，它们应该自动形成平衡。刚体运动抑制 特征假设没有净作用力。如果情况并非如此，我们需要适当的约束来提供平衡所施加的机械力的反作用力。

哪些域应该自动约束？

在具有多个域的装配中，某些域可能没有足够的约束。我们不想人为地约束那些已经有足够约束的域。静态分析的收敛误差并不能帮助我们确定哪些域是稳定的，哪些域是自由悬挂的。

在这种情况下，我们可以执行特征频率分析来找到悬挂域。对应于刚体运动的模式具有接近于零的特征频率。

我们通过使用包含三个矩形域的装配来演示这一点。底部两个域粘合在一起，顶部域挂起。我们对最底部的边界应用固定约束。

有三种频率接近于零的模式，分别对应于悬挂域的三种刚体模式。现在我们已经知道哪个域需要刚体运动抑制。

利用特征频率分析来识别悬挂域。

请注意，这里使用非常粗化的网格就足够了。如果特征频率分析的动机是识别悬挂域，则仅寻求低频模式。为此，足以捕获对象形状的单元就足够了。在随后的静态分析中，我们希望使用足够细化的网格来获得精确的解。

这种悬挂域在接触力学仿真中经常遇到。在物体建立足够的接触以稳定彼此之前，一些物体可以会被悬挂。在接触仿真中，我们一般不会希望这些域留在原位。在这种情况下，我们使用 COMSOL Multiphysics 特征，例如弹簧基础，它可以稳定域，而不会将它们固定在原位。有关详细信息，请参阅结构力学模块用户指南 中的“接触建模”部分。

总结

本文中我们讨论了热膨胀仿真中常见的收敛问题的原因：缺乏位移约束。我们讨论了用于缓解这一问题的手动和自动技术。刚体运动抑制 条件有助于使这个过程自动化，并在处理复杂设置时节省时间。为了识别要添加到刚体运动抑制 节点的域，我们可以在粗化网格上使用特征频率分析。

后续操作

• 尝试操作本文中的教程模型（你需要登录到你的 COMSOL Access 帐户并拥有有效的软件许可证才能下载 MPH 文件）
  • 层合板的热预应力
  • 加热电路
• 阅读以下相关博客文章：
  • 如何分析随温度变化的特征频率
• 了解有关特征频率分析的更多信息