
使用 RF 模块或“波动光学”模块求解电磁波问题时,我们利用的是有限元方法求解 Maxwell 控制方程。本篇博客文章将针对建模、网格剖分、求解和后处理这几个步骤介绍几种方法及其适用范围。
电磁波在频域内模拟问题的控制方程
COMSOL Multiphysics 使用有限元方法在模拟域内求解电磁场。假设角频率已知,为 \omega = 2 \pi f,电磁场随时间呈正弦变化,且材料的所有属性相对于场强呈线性,则三维 Maxwell 控制方程可简化为:
其中的材料属性包括:\mu_r 表示相对磁导率;\epsilon_r 表示相对介电常数; 及 \sigma 表示电导率。
已知真空中光速为 c_0,则可在整个模拟域内对电场 \mathbf{E}=\mathbf{E}(x,y,z) 求解上述方程,其中 \mathbf{E} 为矢量,其分量为 \mathbf {E}=<\mathbf{E}_x,\mathbf{E}_y, \mathbf{E}_z>所有其他物理量(例如磁场、电流和功率流)都可从电场推导出。还可以将上述方程表述为特征值问题,以求解模型的系统谐振频率,而非特定频率下的系统响应。
上述方程可通过有限元方法进行求解。要了解有限元方法的概念性介绍,请阅读弱形式系列博客;要获取相关参考文献,更深入地了解有限元方法在电磁波问题中的细微差别,请阅读 Jin Jian-Ming 教授所著的 The Finite Element Method in Electromagnetics 一书。不过就本篇博客文章而言,我们将有限元方法分解为以下四个步骤:
- 建立模型: 定义求解方程、创建模型几何、定义材料属性、建立金属边界和辐射边界并将模型连接到其他器件。
- 剖分网格: 利用有限元将模型空间离散化。
- 求解:求解一组描述电场的线性方程。
- 后处理:从计算得到的电场结果中提取有用信息。
下面我们将详细介绍这些步骤,并描述每一步可用的选项。
修改控制方程的选项
上面显示的控制方程是 Maxwell 方程的频域形式,这是求解波类型问题的最通用形式。不过,我们可以重新表述这一方程,使之适合几种特殊场景。
先来看一个背景电场已知的模拟域情况,我们要将某个物体放在该背景场中。背景场可以是线偏振平面波、高斯光束或者在自由空间中满足 Maxwell 方程的任何用户定义的一般光束。电场中的物体会干扰电场,导致背景场发生散射。在这种情况下,可以利用散射场 公式求解上述方程,不过电场须替换为:
其中背景电场已知,相对场的作用是,在与背景场叠加后得到的总物理场能满足 Maxwell 控制方程。这里我们要求解的是相对场,而不是总物理场。请注意,相对场不是 散射场。
有关散射场 公式的用法示例,请参考计算完美导体球的雷达截面教程模型,其中探讨了背景平面波中完美导体球的雷达辐射,并将之与解析结果对比。
接下来考虑在二维平面中的建模,这时我们求解 \mathbf{E}=\mathbf{E}(x,y),如果考虑电场在面内或面外的极化,那么可以进一步简化建模的过程。如果是面内极化,则假设 E_z=0,如果是面外极化,则假设 E_x=E_y=0。与求解电场矢量的所有三个分量相比,这样的简化明显减小了求解问题的大小。
要在二维轴对称的平面中建模,我们须求解 \mathbf{E}=\mathbf{E}(r,z),其中矢量 \mathbf{E} 的分量为 < E_r, E_\phi, E_z>,同样,为简化建模,我们可以再次考虑面内极化和面外极化的情况,即分别假设 E_\phi=0 和 E_r=E_z=0。
使用二维 公式或二维轴对称面内 公式时,还可以指定面外波数,它适合在面外传播常数或方位角模数已知的情况下使用。对于二维问题,电场公式可以改为:
对于二维轴对称问题,电场公式可以改为:
其中 k_z 或 m 表示面外波数,这两个参数必须指定。
这种建模方法能大大降低某些模型类型的计算复杂程度。比如,结构为轴对称的喇叭天线虽然在三维中的解各不相同,但都是对已知方位角模式求和得到的。先求解这些面外模态,这其中所需的计算量要小得多,然后根据一组二维轴对称分析得到三维解,具体演示可参考波纹状圆形喇叭天线教程模型。
网格剖分的要求和功能
求解电磁波问题时,一定要考虑网格解析度。处理波类型的相关问题时,只有网格足够精细才能解析所有介质中的波长。这一理念本质上类似于信号处理中的奎斯特频率概念:样本尺寸(有限元网格尺寸)必须至少小于要求解波长的一半。
默认情况下,COMSOL Multiphysics 采用二阶单元离散控制方程。每个波长必须至少包含两个单元才能用于求解问题,但网格如此粗化,相应的精度就会相当糟糕。要对电介质中行波求解,通常每个波长至少包含五个二阶单元。也可以使用一阶和三阶离散化,不过这两种通常用于学术研究,而二阶单元既能达到一定的精度且内存要求不是很高,因此是一个最佳的折中选择。
如今,COMSOL Multiphysics 软件在对域剖分网格时,自动实现每一介质中每个波长包含五个单元这一最低标准,如此视频所示,其中不仅展示了不同电介质域的网格剖分,还实现了完美匹配层域的自动网格剖分。这一新的自动网格剖分功能还能对具有周期性边界条件的问题创建适当的周期性网格,具体案例请参考频率选择面周期性互补开环谐振器教程模型。
至于使用的单元类型,较之六面体单元和棱柱单元(三维中)或矩形单元(二维中),应优先选择四面体单元(三维中)或三角形单元(二维中),因为这样的单元色散误差较少。出现这一差别的原因是,对于四面体单元,一个单元内各个方向上的最大距离几乎相等,然而对于六面体单元,完美立方单元中最短线与最长线之比为 \sqrt3。所以如果波沿对角线穿过六面体单元,则波相的解析结果会出现较大误差。
只有对完美匹配层剖分网格时,或者能大致预知解在一个或两个方向上具有强各向异性时,才需要使用六面体单元、棱柱单元或矩形单元。如果要求解的波由于材料的吸收发生衰减,比如波撞在损耗介质上,那么也需要手动设置有限元网格的集肤深度(通常是边界层网格),如此处所述。
如果材料属性在仿真过程中发生改变,则仍是建议手动剖分网格,而且这种情况下也往往必须这样做。举例来说,在电磁加热模拟过程中,材料属性会随温度变化。那么在求解前,即在网格剖分这一步中,就应当考虑材料属性可能发生的变化,因为与一开始就使用精细划分的网格(足以解析场中可能发生的各种变化)相比,在求解过程中重新剖分网格所需的计算量往往更大。这种情况要求我们利用迭代法,手动剖分网格并求解模型。
频带较宽时,可以从下列三种方法中选择一种进行求解:
- 使用将求解波长最短(最高频)的网格来解析整个频率范围。这种做法能够完全避免重新剖分网格产生的计算成本,但是对低频使用了过于细化的网格。
- 使用参数化求解器,对每一个频率重新剖分网格。如果频率空间中频率的增量相当大,并且网格剖分成本相对较低,则适于采用这种做法。
- 在不同频带使用不同网格。这种做法可以降低网格剖分成本,同时使求解的成本相对较低。它实质上是前两种方法的结合,不过需要用户执行的操作最多。
对于具体模型,要预先判断上述哪种方法最有效很困难。
不管一开始使用的是什么网格,始终要执行网格细化研究,也就是用逐步细化的网格重新运行仿真,并观察解的变化。网格越精细,解就越精确,但计算成本也随之增加。如果网格完全由四面体单元或三角形单元构成,则也可以使用自适应网格细化。
求解器选项
在问题适当定义完毕且域中剖分了网格后,COMSOL Multiphysics 就能收到该信息并生成一个线性方程组,使用直接求解器或迭代求解器求解方程组。这两个求解器差别不大,仅在内存要求和求解时间方面有所不同,不过我们可以使用几个选项使模拟效率更高,因为三维电磁场模型通常需要大量内存来求解。
与迭代求解器相比,直接求解器需要的内存更多,它们用于求解具有周期性边界条件的问题、特征值问题以及所有二维模型。具有周期性边界条件的问题一定要用直接求解器,在许多情况中,COMSOL Multiphysics 软件会自动为其匹配直接求解器。
与迭代求解器相比,使用直接求解器能更快地求解特征值问题,但会消耗更多内存。由此,人们常常倾向于重新表述特征值问题,将其转换为在接近谐振的频率范围内激发的频域问题。在频域内求解时,可以使用内存更省的迭代求解器。然而,如果系统中存在高 Q 因子,则必须要在频率空间的许多点上求解。要了解将特征值问题重新表述为频域问题的示例,请阅读有关计算 RF 线圈的 Q 因子和 Fabry-Perot 腔的 Q 因子这两个案例。
“分析方法论”设置中对应用于频域仿真的迭代求解器定义了三个选项,分别是健壮性(默认设置)、中级 或快速,这三个选项可在物理场接口设置中更改。这三种设置的作用是改变正在使用的迭代求解器类型和收敛公差。当你在解算大多数模型时都会用到这些设置,并进行比较,观察它们在求解时间和精度方面的差别,从中选定最适合自己需要的选项。如果模型中不同材料的介电常数相差非常大 (~100:1),则应选择健壮性 设置,若迭代求解器收敛缓慢,甚至可能需要使用直接求解器。
后处理功能
模型求解完毕后,你希望提取电磁场的计算结果数据。COMSOL Multiphysics 会自动生成电场大小的切面图,除此之外,还可以使用许多其他后处理可视化选项。请参考后处理与可视化手册以及有关后处理的系列博客了解初步的知识,并学习如何创建类似下面两张图那样的图像。
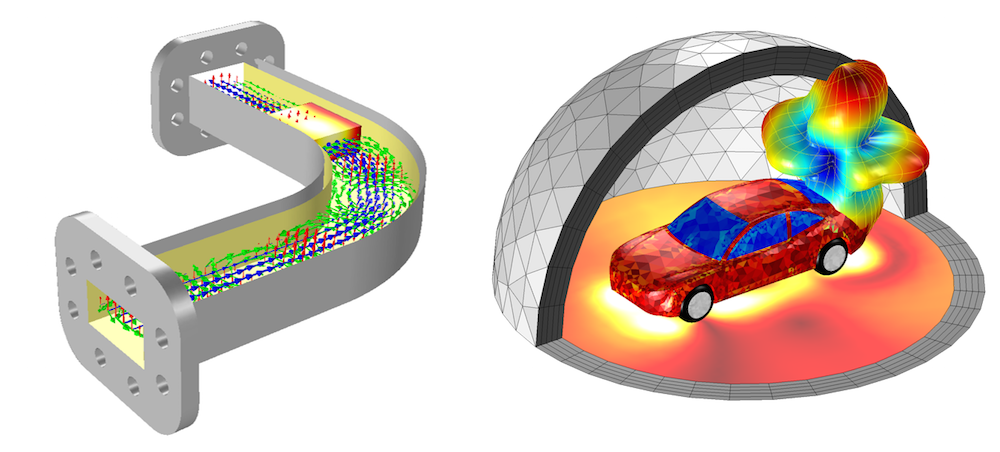
将解物理场、网格及几何都绘制在一张图中,实现极具吸引力的可视化效果。
当然,图像仅表面靓丽是不够的,我们还要从模型中提取数值信息。每次使用端口或集总端口,以及集总端口电流、电压、功率和阻抗时,COMSOL Multiphysics 会自动提供 S 参数。对于含多个端口或集总端口的模型,还能自动创建端口扫描,就像铁氧体环形器教程模型演示的一样,并将结果写入一个 Touchstone 文件。至于特征值问题,会自动计算谐振频率和 Q 因子。
对于天线模型或散射场模型,还能计算并绘制远场辐射方向图、增益图和轴比曲线。

Vivaldi 天线的远场辐射方向图。
此外,还可以在域、边界和边上集成任何派生量以执行一些计算,如计算损耗材料内部散发的热量,或者腔内的总电磁能。当然,在这里我们只列举最常用的后处理功能,还有更多操作等你去尝试。
关于电磁波仿真工具的小结
本文介绍了 Maxwell 控制方程频域形式的多种不同公式,探讨了这些公式如何用于求解电磁波问题以及何时使用。还讨论了网格剖分要求和功能,以及求解模型的不同方法。在这个过程中,还大致概述了后处理功能,以及如何在 COMSOL Multiphysics 中获取数据可视化的信息。
通过学习这些知识,结合阅读有关定义材料属性、建立金属边界和辐射边界以及将模型连接到其他器件的系列博客文章,使你对于在 RF 模块和“波动光学”模块模拟频域电磁波有一个相当完整的了解。当然,本软件提供的相关文档更深入地讲解了全部特征及功能。
如果你对利用 RF 模块或“波动光学”模块满足自己的模拟需求感兴趣,请联系我们。



评论 (2)
gang wu
2017-01-09我在用RF模块三维轴对称仿真光栅时,发现电磁场好像不能穿过对称轴,感觉光场从中间裂开了,不知道什么原因,能不能帮帮我?
宇航 秦
2017-01-10Wu Gang,您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!