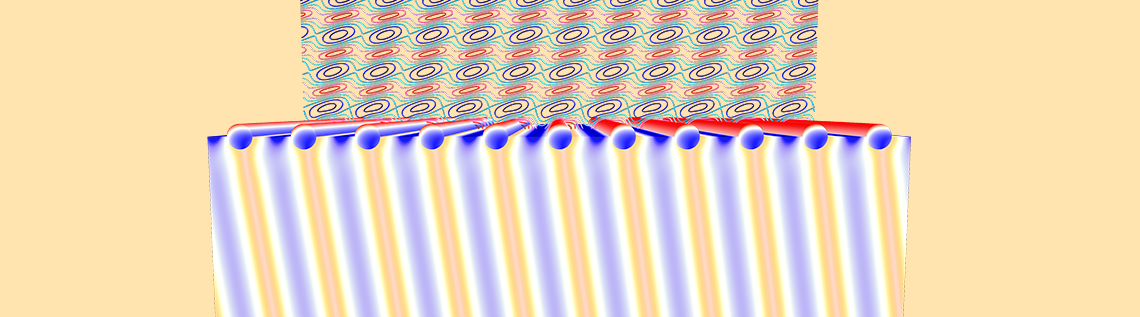
当光入射到玻璃等介电材料表面时，一部分会透射，另一部分则会被反射。有时，我们会在材料中添加一层金属涂层（例如金），它可以改变光的透射率和反射率，并使一部分光被吸收。介电表面和金属涂层的高度和厚度往往随机变化。这篇文章，我们将建立一个数值模型，并对这种情景进行模拟。
一个简单的示例：光学平面
在讨论粗糙的表面之前，我们先来看一个简单的示例：表面镀有一层均匀薄金涂层的光学平面玻璃模型，如下图所示。对于这种模型，其玻璃平面上的结构变化可以忽略。在 COMSOL Multiphysics® 软件中，通过考虑一个宽度远小于波长的二维基本单元，就可以轻松创建这种模型。
此数值模型基于COMSOL 案例库中的一个验证模型：菲涅尔方程，但该模型经过修正，包含一个折射率随波长变化的金镀层。此时需要根据每种材料的最小波长和集肤深度手动调整网格大小，这在之前的博客中已经介绍过了。
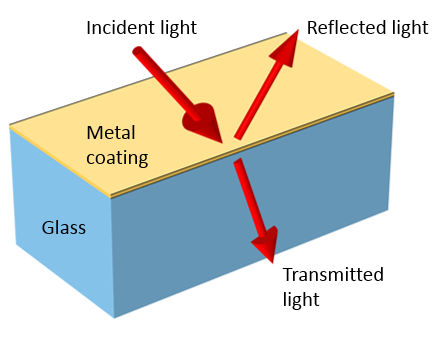
入射到玻璃基底上的金属涂层上的光被反射、透射和吸收。
这个模型包括模拟域左右两侧的 Floquet 周期性边界条件，以及顶部和底部的端口边界条件。顶部的端口边界条件用于在指定的入射角下发射一束平面波，并计算反射光，而底部的边界条件则用于计算透射光。可以通过对金属层内的损失进行积分来计算镀金层内的吸收率。
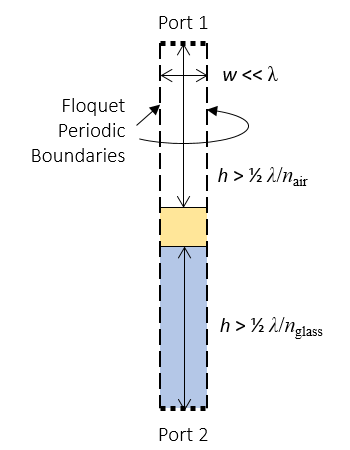
用于计算玻璃表面金属薄层的光学特性的数值模型。
如果对非法线入射角的入射光计算感兴趣，还必须关注模拟域的高度，即材料界面与端口边界条件之间的距离。这个距离必须足够大，以确保模拟域内的任何消逝场都能降低到接近零。
这样做与端口边界条件有关，因为它只能考虑电磁场的传播分量。任何到达端口边界条件的场的消逝分量都会被强制反射，所以必须把端口边界放在距离材料界面足够远的位置。大多数情况下，很难确定消逝场传播多远。一个简单的经验法则是，将端口边界条件放在距离材料界面至少半个波长的地方，并检查增大模拟域是否会对结果产生影响。
下图中的样本结果显示了透射光、反射光和吸收光，以及它们的总和，总和应该始终等于 1。如果总和不等于 1，那么必须仔细检查模型设置。
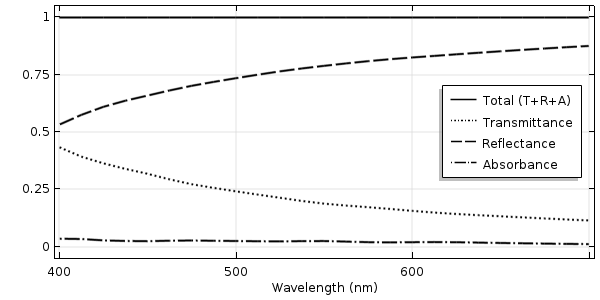
法向入射到含金属涂层的平面玻璃表面的透射光，反射光和吸收光与波长的关系。
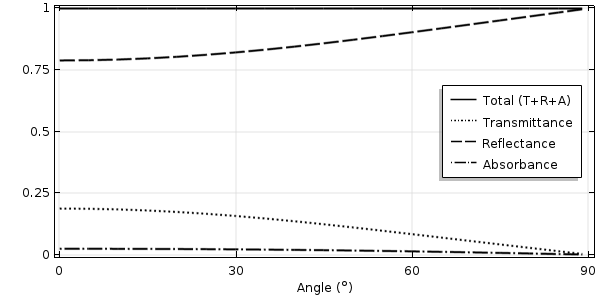
波长为 550 nm 的光在不同入射角下的透射率、反射率和吸收率。
增加复杂性：具有周期性变化的表面
现在，让我们考虑一个更复杂的情况，引入一个周期性的结构变化：正弦波纹。很明显，我们现在需要考虑一个更大的基本单元来表征一个基本波纹。
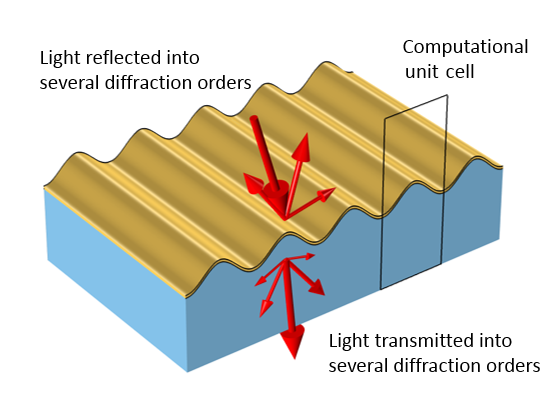
具有周期性变化的表面将光反射和透射成几个不同的衍射级。
我们仍然可以应用与上一个示例中相同的域属性和所有边界条件。但是，如果间距足够大，就会发生高阶衍射。也就是说，光可以被反射和传输到几个不同的方向。为了正确计算反射和透射，需要增加几个衍射级端口。COMSOL软件会根据域的宽度、材料属性和指定的入射角计算出适当的端口数量。如果研究的是入射角的范围，那么必须确保能计算出角度扫描范围内的所有衍射级。
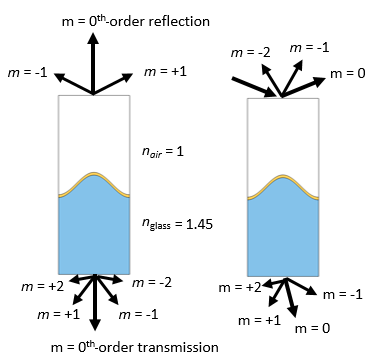
允许存在多个衍射级，具体取决于波长与域宽、折射率和入射角的比值。
在表面等离激元线光栅案例模型中，我们已经深入介绍过高阶衍射产生的条件及相应的模拟过程，此处不再赘述。简单来说，相对于上部和底部材料的波长而言，计算域越宽，可能出现的衍射级越多(衍射级数随入射角变化)。下图绘制了总的透射率和反射率，即不同衍射级的所有反射光和所有透射光的总和。
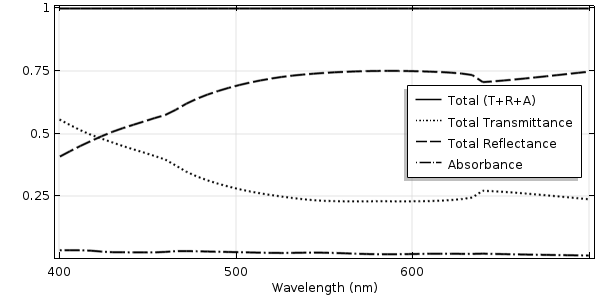
法向入射到有金属涂层的波纹玻璃表面的光的透射率，反射率和吸收率。
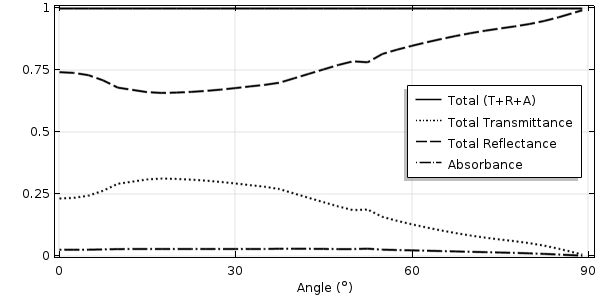
550nm 光在不同入射角下的透射率、反射率和吸光率。
求解一个更难的案例：具有随机粗糙度的表面
现在，我们来讨论计算上最困难的情况：高度上存在随机变化的表面。为了模拟这种随机性，我们必须构建多个不同宽度和不同粗糙轮廓的模拟域。随着模拟域宽度的增加，以及对不同表面轮廓子集的采样，由不同的模型计算出的平均行为将逐渐收敛。也就是说，通过对粗糙表面进行采样来产生一组统计数据。在这里，对于这些计算数据的统计处理，我们不做详细介绍，关于如何将表面高度定义为一组幅值和相位随机变化的不同正弦波的总和，来模拟一个近似粗糙表面的域，具体可以参考这篇博客。
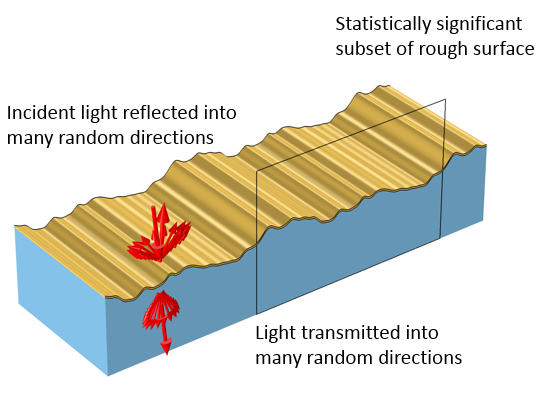
一个随机变化的粗糙表面在随机方向上反射和透射光。模型必须在粗糙轮廓上采集一个统计意义上的子集样进行计算。
计算域必须非常宽，其长度远大于波长。我们仍然希望模拟平面波以不同角度入射到结构上，因此使用了 Floquet 周期性边界条件，这要求在周期性边界上采用有相同的网格划分。实际上，这意味着我们可能需要对域的几何形状进行稍微调整，以确保左右两边的边界相同。如果我们采用这篇博客中所述的正弦函数的总和，轮廓将自动呈现周期性。
同样，我们仍然希望使用端口边界条件来激励波。然而，使用衍射级端口来监测反射和透射光已经不再实际了，因为这可能会导致数百(或数千)个衍射级。此外，由于这个模型代表一个统计样，因此我们对散射到不同级的光的相对分数并不感兴趣，我们只关注反射光和透射光的总和。也就是说，这种模拟方法计算的是总积分散射加上表面的镜面反射和透射之和。
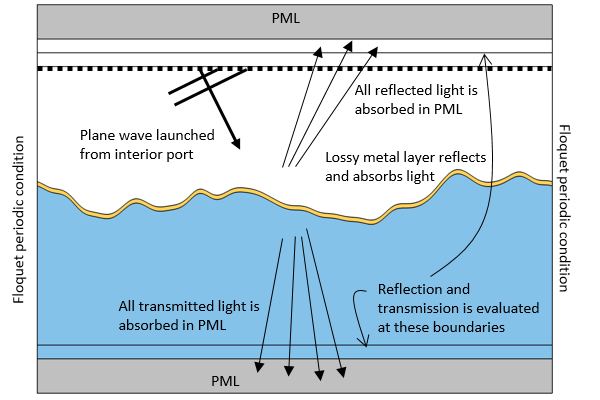
一个粗糙表面模型的计算域。光从内部端口向材料界面发射。反射回这个端口的光穿过它并在完美匹配层中被吸收，透射光也是如此。添加两个额外的边界来监测总反射率和透射率。
因此，我们引入了一个替代的模拟策略，即不使用端口计算反射和传输，而是在上表面和下表面使用完美匹配层来吸收所有的反射光和透射光，并使用探针计算反射率和透射率。完美匹配层吸收任何入射到其上的场，具体可以参考这篇关于使用完美匹配层处理波电磁学问题的博客。
完美匹配层会同时吸收场的传播和消逝分量，但我们希望它只吸收传播分量。因此，需要再次确保把完美匹配层放在远离材料界面的位置。使用与之前经验法则的相同，即将完美匹配层放在离材料界面至少半个波长的地方。
当接近掠射角入射时，即使是完美匹配层域也不会默认吸收所有的光。在近乎掠射的角度下，吸收方向的有效波长非常长，需要修改完美匹配层设置中的默认波长（如下图所示）。只有当我们对大于约 75° 的入射角感兴趣时，才有必要进行这种设置修改。
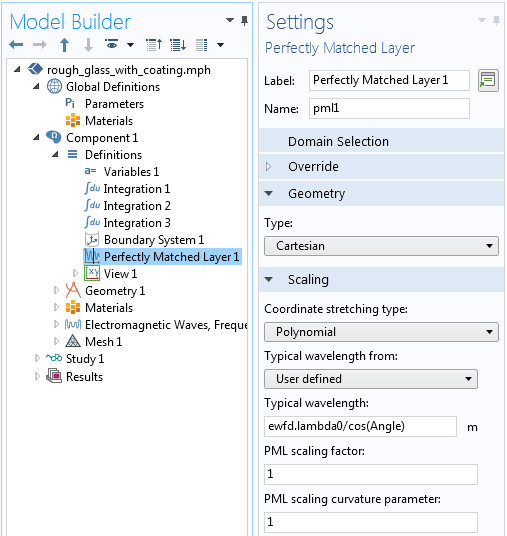
修改完美匹配层设置，以考虑入射角的掠射角。
由于域被上下完美匹配层所限定，所以发射波的端口必须放在模拟域内。为此，使用狭缝条件来定义一个以域为背景的内部端口。也就是说这个端口现在从这个内部边界向一个方向发射波。任何反射回边界的光都会无障碍地通过，然后被完美匹配层吸收。
尽管这是发射波的一个好方法，但我们不再使用端口边界条件计算有多少光被反射，因为这需要添加数百个衍射端口，同样的，也需要添加数百个端口来计算总透射率。
在入射侧，将监测边界放在内部端口的上方。发射口引入了一个向材料界面传播的平面波。在界面上反射的光通过这个内部端口，然后通过监测反射率的边界，在完美匹配层中被吸收。
在入射侧，把这个监测边界放在内部端口的上方。在发射口引入了一个向材料界面传播的平面波。在界面上反射的光通过这个内部端口，然后通过监测反射率的边界，并在完美匹配层中被吸收。
下图显示了透射率、反射率和吸收率的样本计算结果。这些结果与光滑表面和周期性变化表面的结果明显不同。请注意，入射角的扫描在偏离法线 85° 时终止。当然，对于模拟的不同的随机几何，这些结果会略有不同。
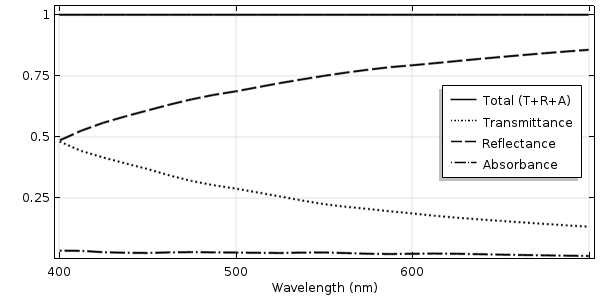
法向入射到粗糙玻璃表面的透射率、反射率和吸收率。
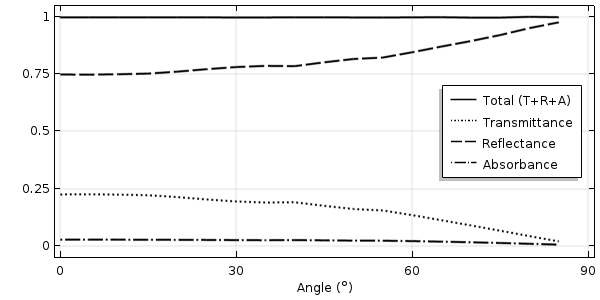
在入射角不超过 85° 的情况下，波长为 550nm 光的透射率、反射率和吸收率。
关于计算粗糙表面的光学特性的总结
本文介绍了一种适用于计算粗糙表面光透射和反射的模拟方法，并将这种方法与均匀光学平面的模拟方法以及周期性变化表面的模拟方法进行对比。粗糙表面的模拟方法也可用于计算具有长周期的周期性结构，例如不需要关注散射到不同的衍射级时。
对模拟真正的随机表面时，确实需要格外小心，因为需要调整几何形状以确保其周期性。另外，所研究的域大小和不同的随机几何形状的数量都必须足够大，以获得具有统计意义的结果。由于这需要求解同一模型的许多不同变体，并对结果进行后处理，因此在模拟流程中使用 App 开发器、LiveLink™ for MATLAB® 或 LiveLink™ for Excel®将非常有帮助。
更多资源
- 了解如何使用COMSOL生成一个粗糙表面
- 查看如何使用不同方法生成随机几何对象
- 查看其他与波动光学有仿真相关的博客：
MATLAB 是 The MathWorks, Inc. 的注册商标。Microsoft 和 Excel 是微软公司在美国和/或其他国家的注册商标或商标。
评论 (0)